Contents

Theorie

Theorie

%pylab inline
%config InlineBackend.figure_format = 'svg'

%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib

Quellen

  • Dietmaier: Mathematik für Angewandte Wissenschaften

    • 7.4 Fourierreihen

    • 13.1 Fouriertransformation

  • Papula:

    • Band 2, II, 1 und 2, p. 163 bis 190

    • Klausur- und Übungsaufgaben

    • Anwendungsbeispiele

Theorie - Zusammenfassung

Ziel: Überlagerung von und Zerlegung/Entwicklung in harmonischen Schwingungen

Vergleiche bisherige Zerlegungen/Entwicklungen

  • Zerlegung einer Kraft in vorgegebene Richtungen (z.B. Tangential- und Normalrichtung)

  • Zerlegung/Entwicklung einer Funktion an einer Stelle in ein Polynom, d.h. in Potenzenanteile: Taylorreihe

Fourierreihe

Entwicklung einer periodischen Funktion in harmonische Schwingungen der selben Periode, genannt harmonische oder Fourier-Analyse.

Sinus und Cosinus

x = linspace(-2*pi, 2*pi, 500)
figure(figsize=(8, 8))

subplot(2,1,1)
vlines(-pi, -1, 1, linestyle='--')
vlines( pi, -1, 1, linestyle='--')
plot(x, sin(1*x), label="sin(1*x)")
plot(x, sin(2*x), label="sin(2*x)")
plot(x, sin(3*x), label="sin(3*x)")
legend(loc='best')
xlabel('x')
grid(True)

subplot(2,1,2)
vlines(-pi, -1, 1, linestyle='--')
vlines( pi, -1, 1, linestyle='--')
plot(x, cos(0*x), label="cos(0*x)")
plot(x, cos(1*x), label="cos(1*x)")
plot(x, cos(2*x), label="cos(2*x)")
plot(x, cos(3*x), label="cos(3*x)")
legend(loc='best')
xlabel('x')
grid(True)
_images/FT_Theorie_3_0.svg

Periode \(2\pi\)

\[\begin{split}\begin{align} \int_{-\pi}^{\pi} \cos(nx) \text{d}x &= 0 \text{ für alle } n>0\\ \text{für } n=0 \text{ gilt } \int_{-\pi}^{\pi} \cos(0x) \text{d}x &= \int_{-\pi}^{\pi} \text{d}x = 2\pi \\ \int_{-\pi}^{\pi} \cos(nx) \cos(mx) \text{d}x &= 0 \text{ für } n\neq m \text{ und } \pi \text{ für } n=m \\ \int_{-\pi}^{\pi} \sin(nx) \text{d}x &= 0 \text{ für alle } n\geq 0\\ \int_{-\pi}^{\pi} \sin(nx) \sin(mx) \text{d}x &= 0 \text{ für } n\neq m \text{ und } \pi \text{ für } n=m \\ \int_{-\pi}^{\pi} \sin(nx) \cos(mx) \text{d}x &= 0 \text{ für alle } n, m \end{align}\end{split}\]

Fourierreihe:

\[f(x) = \frac{a_0}{2} + \sum_{n=1}^\infty a_n \cos(nx) + \sum_{n=1}^\infty b_n \sin(nx)\]

Fourierkoeffizienten:

\[\begin{split}\begin{align} a_0 & = \frac{1}{\pi}\int_0^{2\pi} f(x) dx\\ a_n & = \frac{1}{\pi}\int_0^{2\pi} f(x) \cos(nx) dx \text{ für } n\geq 1\\ b_n & = \frac{1}{\pi}\int_0^{2\pi} f(x) \sin(nx) dx \text{ für } n\geq 1 \end{align}\end{split}\]

allgemeine Periode \(T\)

Fourierreihe:

\[f(x) = \frac{a_0}{2} + \sum_{n=1}^\infty a_n \cos(n\omega x) + \sum_{n=1}^\infty b_n \sin(n\omega x)\]

Kreisfrequenzen: \(\omega = \frac{2\pi}{T}\), \(2\omega\), \(3\omega\), \(4\omega\), …

  • Die Kreisfrequenz \(\omega\) heißt Grundkreisfrequenz oder Kreisfrequenz der Grundschwingung.

  • Für \(n>1\) heißen die \(n\omega\) Kreisfrequenzen der Oberschwingungen.

Fourierkoeffizienten: Integrale über eine Periodendauer, z.B. von 0 bis \(T\).

\[\begin{split}\begin{align} a_0 & = \frac{2}{T}\int_0^T f(x) dx\\ a_n & = \frac{2}{T}\int_0^T f(x) \cos(n\omega x) dx \text{ für } n\geq 1\\ b_n & = \frac{2}{T}\int_0^T f(x) \sin(n\omega x) dx \text{ für } n\geq 1 \end{align}\end{split}\]

Symmetrien

  • Falls \(f\) eine gerade Funktion ist, dann gilt \(b_n=0\) für alle \(n= 1,2,3,...\).

  • Falls \(f\) eine ungerade Funktion ist, dann gilt \(a_n=0\) für alle \(n= 0, 1,2,3,...\).

  • Die Integrale können über jedes Intervall, dessen Länge die Periode ist, ausgeführt werden. Also z.B. \(\int_{-\pi}^{\pi}\) statt \(\int_0^{2\pi}\).

Komplexe Darstellungen

  • Periode \(2\pi\):

    • Fourierreihe:

      \[f(x) = \sum_{n=-\infty}^{\infty} c_ne^{inx}\]

    • Fourierkoeffizienten:

      \[c_n = \frac{1}{2\pi}\int_0^{2\pi} f(x)e^{-inx} dx\]

  • allgemeine Periode \(T\):

    • Fourierreihe:

      \[f(x) = \sum_{n=-\infty}^{\infty} c_ne^{in\omega x}\]

    • Fourierkoeffizienten:

      \[c_n = \frac{1}{T}\int_0^T f(x)e^{-in\omega x} dx\]

  • Zusammenhang zwischen reellen und komplexen Koeffizienten:

    • \(c_0 = \frac{a_0}{2}\)

    • \(c_n = \frac{1}{2}(a_n - ib_n)\) für \(n\geq 1\)

    • \(c_{-n} = \frac{1}{2}(a_n + ib_n)\) für \(n\geq 1\)

Fouriertransformation

\[\begin{split}\begin{align} F(\omega) & = \mathcal{F}\left\{f\right\}(\omega) = \int_{-\infty}^{\infty}f(t)e^{-i\omega t}dt\\ f(t) & = \mathcal{F}^{-1}\left\{F\right\}(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega t}d\omega \end{align}\end{split}\]

Eigenschaften:

  • Linearität

  • Zeit- und Frequenzverschiebungen

  • Modulation

  • Ableitung

  • Faltung

Anwendungen

  • Signalanalyse, Elektrotechnik, Übertragungssysteme, Frequenzgang, Impedanzen

  • Diskrete Fouriertransformation (DFT)

  • Partielle DGL

Computer

SymPy Befehle:

import sympy as sp
from sympy.integrals import fourier_transform, inverse_fourier_transform

sp.init_printing(use_unicode=True, use_latex=True)

t, k = sp.symbols('t k')
a    = sp.symbols('a', positive=True)

fourier_transform(sp.Heaviside(t)*sp.exp(-a*t), t, k)
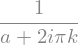
_images/FT_Theorie_9_0.png 
sp.init_printing(False)

Aufgaben

Aufgabe 1: Fourierreihe einer Sägezahnfunktion

Die Sägezahnfunktion ist gegeben durch die periodische Fortsetzung von \(f(x) = x\) für \(-\pi \leq x < \pi\). Berechnen Sie die Koeffizienten der Fourierreihe.

Quelle: Dietmaier, p. 283, Beispiel 7.12 Fourierentwicklung einer Sägezahnfunktion

Lösung: Die Fourierkoffizienten sind:

  • \(a_n = 0\)

  • \(b_n = \frac{2}{n}(-1)^{n+1}\)

# Sägezahnfunktion:
x = linspace(-3*pi, 3*pi, 3000)
y1 = linspace(-pi, pi, 1000)
y  = concatenate((y1,y1,y1))

# Fourierreihe:
N = 10   # Anzahl harmonische Schwingungen
yf = zeros(shape(y))
for n in range(1, N+1):
    yf = yf + 2/n*(-1)**(n+1)*sin(n*x)

# Plot:
figure(figsize=(7,4))
plot(x, y , '-', label='Saegezahnfunktion')
plot(x, yf, '-', label='Fourierreihe bis N=%d' %N)
legend(loc='best')
grid(True)
_images/FT_Theorie_13_0.svg

Aufgabe 2: Fourierreihe einer Rechteckfunktion

Die Rechteckfunktion \(f\) mit Periode \(2\pi\) ist im Bereich \([0,2\pi]\) gegeben durch

\[\begin{split}f(x)= \begin{cases} 1 & \text{ für } 0 \leq x \leq \pi \text{ und}\\ -1 & \text{ für } \pi\leq x \leq 2\pi. \end{cases}\end{split}\]

  1. Erstellen Sie einen Plot der Rechteckfunktion im Bereich \([0,4\pi]\).

  2. Berechnen Sie die Koeffizienten der Fourierreihe von \(f\) und erstellen Sie einen stem-Plot der Koeffizienten.

  3. Fügen Sie Ihrem Plot die Fourierreihe von \(f\) bis zur fünften Oberschwingung hinzu.

Quelle: Papula, Band 2, II, 1, p.171ff.

Lösung:

Die Fourierkoffizienten sind:

  • \(a_n = 0\)

  • \(b_n = \frac{2}{n\pi}(1 - \cos(n\pi))\), d.h. \(b_n = 0\) falls \(n\) gerade und \(b_n = \frac{4}{n\pi}\) falls \(n\) ungerade.

# Rechteckfunktion:
x  = linspace(0, 4*pi, 400)
y1 = ones(100)
y  = concatenate((y1, -y1, y1, -y1))

# Fourierreihe:
N = 50   # Anzahl harmonische Schwingungen
yf = zeros(shape(y))
for n in range(1, N+1):
    bn = 2/(n*pi)*(1 - (-1)**n)
    yf = yf + bn*sin(n*x)

# Plots:
figure(figsize=(7,6))
subplot(2,1,1)
plot(x, y , '-', label='Rechteckfunktion')
plot(x, yf, '-', label='Fourierreihe bis N=%d' %N)
legend(loc='best')
grid(True)

subplot(2,1,2)
n = arange(1, N+1)
bn = 2/(n*pi)*(1 - (-1)**n)
stem(n, bn, use_line_collection=True)
ylim(-0.1,1.5)
grid(True)
_images/FT_Theorie_15_0.svg

Aufgabe 3: Fourierreihe einer anderen Rechteckfunktion

Ein Signal mit Periode 2 ist gegeben durch \(f(x) = 1\) für \(0 \leq x \leq 1\) und \(f(x) = 0\) für \(1 < x \leq 2\).

  1. Skizzieren Sie das Signal.

  2. Bestimmen Sie die Fourierreihe des Signals.

Lösung: \(\omega_0 = \frac{2\pi}{T}\), \(f(x) = \frac{a_0}{2} + \sum_{n=1}^\infty a_n \cos(n\omega_0 x) + \sum_{n=1}^\infty b_n \sin(n\omega_0x)\)

  • \(a_0 = \frac{2}{T}\int_0^T f(x) dx = 1\)

  • \(a_n = \frac{2}{T}\int_0^T f(x) \cos(n\omega_0 x) dx= 0\)

  • \(b_n = \frac{2}{T}\int_0^T f(x) \sin(n\omega_0 x) dx = \frac{1}{n\pi}[1 - (-1)^n]\)

Aufgabe 4: Fourierreihe einer Sägezahnfunktion

Eine Sägezahnfunktion mit Periode \(2\pi\) hat im Bereich \(0 \leq x < 2\pi\) die Funktionsgleichung \(f(x) = 2\pi x\).

  1. Erstellen Sie eine Skizze des Funktionsgraphen im Bereich \([-2\pi, 4\pi]\).

  2. Bestimmen Sie die reellen Koeffizienten der zugehörigen Fourierreihe.

Quelle: Papula, Klausur- und Übungsaufgaben, p. 243f., D41

Lösung:

\[f(x) = \frac{a_0}{2} + \sum_{n=1}^\infty a_n \cos(nx) + \sum_{n=1}^\infty b_n \sin(nx)\]

mit

\[\begin{split}\begin{align} a_0 & = \frac{1}{\pi}\int_0^{2\pi} f(x) dx\\ a_n & = \frac{1}{\pi}\int_0^{2\pi} f(x) \cos(nx) dx \text{ für } n\geq 1\\ b_n & = \frac{1}{\pi}\int_0^{2\pi} f(x) \sin(nx) dx \text{ für } n\geq 1 \end{align}\end{split}\]

ergibt \(a_0 = 4\pi^2\), \(a_n = 0\) und \(b_n = -4\pi\frac{1}{n}\)

Aufgabe 5: Fourierreihe einer weiteren Rechteckfunktion

Ein Signal mit Periode \(2\pi\) ist gegeben durch \(f(x) = 1\) für \(0 \leq x \leq \pi\) und \(f(x) = 0\) für \(\pi < x \leq 2\pi\).

  1. Skizzieren Sie das Signal.

  2. Bestimmen Sie die Fourierreihe des Signals.

Lösung:

\(f(x) = \frac{a_0}{2} + \sum_{n=1}^\infty a_n \cos(n x) + \sum_{n=1}^\infty b_n \sin(nx)\)

  • \(a_0 = 1\)

  • \(a_n = 0\)

  • \(b_n = \frac{1}{n\pi}[1 - (-1)^n]\)

Aufgabe 6: Fourierreihe

Gegeben ist ein periodisches Signal mit Periode \(4\pi\). Im Bereich \(-2\pi \le x \le 2\pi\) hat es folgende Form:

\[\begin{split}f(x) = \begin{cases} 0 \quad & -2\pi \le x \le -\pi \\ 1 \quad & -\pi \le x \le \pi \\ 0 \quad & \pi \le x \le 2\pi \end{cases}\end{split}\]

  1. Skizzieren Sie das Signal.

  2. Bestimmen Sie die Fourierkoeffizienten.

Lösung:

Periodendauer: \(T = 4\pi\), Kreisfrequenz: \(\omega_0 = \frac{2\pi}{T} = 0.5\)

da gerade Funktion \(b_n = 0\)

\[\begin{split}\begin{align} a_0 & = \frac{2}{T} \int_{-\pi}^{\pi}1 \,\text{d}x = \frac{1}{2 \pi}\left(\pi+\pi\right) = 1 \\[3ex] a_n & = \frac{2}{T} \int_{-\pi}^{\pi} \cos\left(n \omega_0 x\right) \,\text{d}x = \frac{1}{2\pi} \int_{-\pi}^{\pi} \cos\left(\frac{n x}{2}\right) \,\text{d}x = \frac{1}{2\pi}\left(\sin\left(\frac{n x}{2}\right) \frac{2}{n}\right)_{-\pi}^{\pi} \\[2ex] & = \frac{1}{n\pi}\left(\sin\left(\frac{n \pi}{2}\right) - \sin\left(-\frac{n \pi}{2}\right) \right) = \frac{1}{n\pi}\left(\sin\left(\frac{n \pi}{2}\right) + \sin\left(\frac{n \pi}{2}\right) \right) = \frac{2}{n\pi}\sin\left(\frac{n \pi}{2}\right) \end{align}\end{split}\]

previous

Fouriertransformation

next

Numerik