Laplacetransformation¶

%pylab inline

import sympy as sp
from scipy.integrate import odeint

%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib

# set default values for plotting:
rcParams['axes.titlesize']  = 14
rcParams['axes.labelsize']  = 14
rcParams['xtick.labelsize'] = 14
rcParams['ytick.labelsize'] = 14
rcParams['legend.fontsize'] = 12
rcParams['lines.linewidth'] = 2

Literatur¶

Nise: Control Systems Engineering, Chapter 2 Modeling in the Frequency Domain
Dietmaier: Mathematik für Angewandte Wissenschaften, 13.2 Laplacetransformation
Papula: Band 2, VI, Laplace-Transformationen
Bronson, Costa: Differential Equations, Chapters 21 to 25
MacCluer: Chapter 10 Frequency-Domain Methods

Theorie - Zusammenfassung¶

Idee¶

Löse DGL im Zeitbereich durch

Laplace-Transformation der DGL in den Frequenzbereich
Lösen der entsandenen algebraischen Gleichung im Frequenzbereich
Rücktransformation der Lösung in den Zeitbereich mit Hilfe von evtl. Partialbruchzerlegung und Korrespondenztabellen

Definition¶

Für eine Funktion \(f(t)\) im Zeitbereich ist die Laplace-Transformation \(F(s) = \mathcal{L}\left\{f\right\}(s)\) im Frequenzbereich durch folgende Integraltransformation definiert:

\[F(s) = \mathcal{L}\left\{f\right\}(s) = \int_{0}^{\infty} e^{-st} f(t) \,\mathrm{d}t, \quad s\in\mathbb{C}.\]

Die Laplace-Transformation verwendet nur die Werte der Funktion \(f(t)\) für Zeiten \(t\geq 0\). Sie ist im Allgemeinen nicht für jedes \(s\) definiert.

Eigenschaften¶

Beispiele von Eigenschaften:

Die Laplace-Transformation ist linear: \(\mathcal{L} \left\{\alpha f + \beta g\right\} = \alpha\mathcal{L}\left\{f\right\} + \beta\mathcal{L}\left\{g\right\}\)
Der Ableitung im Zeitbereich entspricht eine Multipliaktion mit \(s\) minus Anfangswert \(f(0)\): \(\mathcal{L}\left\{\dot{f}\right\}(s) = s \mathcal{L}\left\{f\right\}(s) - f(0)\) Deshalb wird eine DGL im Zeitbereich zu einer algebraischen Gleichung im Frequenzbereich.

Korrespondenztabellen¶

Zeitbereichfunktion \(f(t)\)	Laplace-Transformierte \(F(s)\)
\(af(t) + bg(t)\)	\(aF(s) + bG(s)\)
\(\dot{f}(t)\)	\(sF(s) - f(0)\)
\(\ddot{f}(t)\)	\(s^2F(s) - sf(0) - \dot{f}(0)\)
\(f(t-a)\)	\(e^{-as}F(s)\)
\(e^{-at}f(t)\)	\(F(s+a)\)
\(\int_0^t f(\tau)d\tau\)	\(\frac{F(s)}{s}\)
\(f(t)*g(t)\)	\(F(s)G(s)\)
\(f(at)\)	\(F(\frac{s}{a})\frac{1}{a}\)
\(1\) (Heavisidefunktion)	\(1/s\)
\(\delta(t)\) (Diracfunktion)	\(1\)
\(t^n\)	\(n!/s^{n+1}\)
\(e^{-at}\)	\(1/(s+a)\)
\(\cos(at)\)	\(s/(s^2 + a^2)\)
\(\sin(at)\)	\(a/(s^2 + a^2)\)
\(\cosh(at)\)	\(s/(s^2 - a^2)\)
\(\sinh(at)\)	\(a/(s^2 - a^2)\)

Mehr Eigenschaften und Korrespondenztabellen z.B. unter hier.

Partialbruchzerlegung¶

Die Partialbruchzerlegung wird oft verwendet, um die Lösung im Frequenzbereich in eine Summe von Brüchen zu zerlegen, deren Rücktransformationen bekannt sind.

Anwendungen¶

Lösen von GDGL \(n\)-ter Ordnung
Lösen von Systemen GDGL
Regelungstechnik: Blockdiagramme, Übertragungsfunktionen, Sprungantwort, elektrische Schaltungen, Impedanz etc.

Computer¶

SymPy Befehle:

laplace_transform: This function returns (F, a, cond) where F is the Laplace transform of f, Re(s)>a is the half-plane of convergence, and cond are auxiliary convergence conditions.
inverse_laplace_transform

import sympy as sp
from sympy.integrals import laplace_transform, inverse_laplace_transform

sp.init_printing(use_unicode=True, use_latex=True)

t, s = sp.symbols('t s')
a    = sp.symbols('a', positive=True)

laplace_transform(1, t, s)[0]

_images/RT_Laplacetransformation_15_0.png

Heaviside-Funktion:

sp.Heaviside(t)

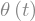
_images/RT_Laplacetransformation_17_0.png

laplace_transform(sp.Heaviside(t), t, s)[0]

_images/RT_Laplacetransformation_18_0.png

laplace_transform(sp.exp(-a*t), t, s)[0]

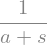
_images/RT_Laplacetransformation_19_0.png

inverse_laplace_transform(a/(s**2 + a**2), s, t)

_images/RT_Laplacetransformation_20_0.png

inverse_laplace_transform(1/(s*(s + 2)), s, t)

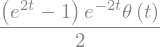
_images/RT_Laplacetransformation_21_0.png

sp.init_printing(False)

Aufgaben¶

Siehe auch Quellen oben, z. B.

Papula: Klausur- und Übungsaufgaben, G, 5 Lösung linearer Anfangswertprobleme mit Hilfe der Laplace-Transformation, p.440 ff.
Papula: Anwendungsbeispiele, XII, Laplace-Transformationen, p. 416 ff.

Aufgabe 1: GDGL mit Laplacetrafo¶

Löse \(\ddot{y} + 3\dot{y} + 2y = 1\) mit Null-Anfangsbedingungen \(y(0)=0\) und \(\dot{y}(0)=0\) mittels Laplace-Transformation.

Quelle: MacCluer: Industrial Mathematics. p. 150.

Lösung: \(y(t) = \frac{1}{2} - e^{-t} + \frac{1}{2}e^{-2t}\)

Aufgabe 2: GDGL System mit Laplacetrafo¶

Löse das DGL-System

\[\begin{split} \begin{align*} \dot{x} & = -2x - 9y \\ \dot{y} & = x - 2y \end{align*} \end{split}\]

mit den Anfangsbedingungen \(x(0)=-1\) und \(y(0)=1\) mittels Laplace-Transformation.

Quelle: MacCluer: Industrial Mathematics. p. 151 f.

Lösung:

\[\begin{split} \begin{align*} x(t) & = -e^{-2t}\cos(3t) - 3e^{-2t}\sin(3t) \\ y(t) & = e^{-2t}\cos(3t) - \frac{1}{3}e^{-2t}\sin(3t) \end{align*} \end{split}\]

Aufgabe 3: Übertragungsfunktion, Sprungantwort¶

Bestimmen Sie die Übertragungsfunktion der DGL \(\dot{c}(t) + 2c(t) = r(t)\) mit Null-Anfangsbedingungen.
Sprungantwort: Bestimmen Sie die Antwort \(c(t)\) des Systems auf die Einheitsstufenfunktion \(r(t) = 1\) für \(t\geq 0\) und \(r(t) = 0\) für \(t<0\) und Null-Anfangsbedingungen.

Quelle: Nise, Control Systems Engineering, Examples 2.4 and 2.5

Lösung:

Die DGL hat die Laplace-Transformation \(sC(s) + 2C(s) = R(s)\). Die Übertragungsfunktion lautet \(G(s) = \frac{C(s)}{R(s)}= \frac{1}{s + 2}\).
\(c(t) = \frac{1}{2}(1 - e^{-2t})\)

Aufgabe 4: Übertragungsfunktion und DGL¶

Bestimmen Sie die Übertragungsfunktion der DGL \(\frac{\text{d}^3c}{dt^3} + 3\frac{\text{d}^2c}{dt^2} + 7\frac{\text{d}c}{dt} +5c = \frac{\text{d}^2r}{dt^2} + 4\frac{\text{d}r}{dt} + 3r\) mit Null-Anfangsbedingungen.
Welcher DGL entspricht die Übertragungsfunktion \(G(s) = \frac{2s +1}{s^2 + 6s + 2}\)?

Quelle: Nise, Control Systems Engineering, Skill-Assessment Exercise 2.3 and 2.4

Lösung:

\(G(s) = \frac{C(s)}{R(s)} = \frac{s^2 + 4s + 3}{s^3 + 3s^2 + 7 s+ 5}\)
\(\frac{\text{d}^2c}{dt^2} + 6\frac{\text{d}c}{dt} +2c = 2\frac{\text{d}r}{dt} + r\) mit Null-Anfangsbedingungen

Aufgabe 5: RLC-Schaltungen und Impedanzen¶

Impedances of resistor, capacitor and inductor:

component	voltage \(v(t)\) from current \(i(t)\)	current \(i(t)\) from voltage \(v(t)\)	impedance \(Z(s) = \frac{V(s)}{I(s)}\)
resistor	\(v(t) =R i(t)\)	\(i(t) = \frac{1}{R}v(t)\)	R
capacitor	\(v(t) = \frac{1}{C}\int_0^t i(\tau) \text{d} \tau\)	\(i(t)=C\frac{\text{d}v(t)}{\text{d}t}\)	\(\frac{1}{Cs}\)
inductor	\(v(t) = L\frac{\text{d} i(t)}{\text{d}t}\)	\(i(t)= \frac{1}{L}\int_0^t v(\tau) \text{d} \tau\)	\(Ls\)

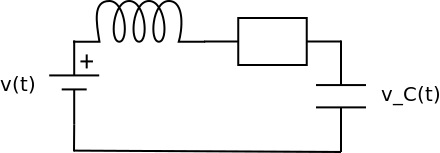
Nise Ex 2.6

Assuming zero initial conditions, find the transfer function relating the capacitor voltage \(V_C(s)\) to the input voltage \(V(s)\) by

first determining the differential equation relating \(v_C(t)\) to \(v(t)\) and then transforming it to the frequency domain.
using impedances and Kirchhoff’s laws in frequency domain.

Quelle: Nise: Control Systems Engineering. Section 2.4 and Examples 2.6 and 2.7

Aufgabe 6: Zeit- und Frequenzbereich¶

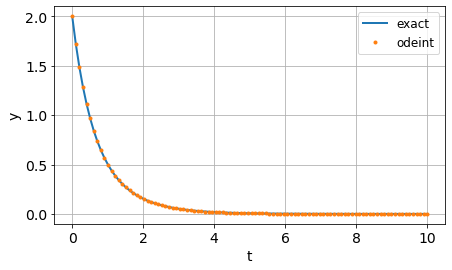
Lösen Sie die Differentialgelichung \(\ddot{y} + 3\dot{y} + 2y = 0\) mit den Anfangsbedingungen \(y(0)=2\) und \(\dot{y}(0)= -3\)

im Zeitbereich mit den Methoden aus dem Abschnitt GDGL,
im Frequenzbereich mittels Laplace-Transformation

und überprüfen Sie Ihr Ergebnis am Computer.

Quelle: Holzner: Differential Equations for Dummies. p. 245 ff.

Lösung: \(y(t) = e^{-t} + e^{-2t}\)

sp.init_printing()

t = sp.symbols('t')
y = sp.symbols('y', cls=sp.Function)
diffeq = sp.Eq(y(t).diff(t).diff(t) + 3*y(t).diff(t) + 2*y(t), 0) 
diffeq

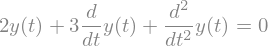
_images/RT_Laplacetransformation_30_0.png

ys = sp.dsolve(diffeq, y(t))
ys

_images/RT_Laplacetransformation_31_0.png

sp.init_printing(False)

t = linspace(0, 10, 100)
y0 = array([2, -3])

A = array([[ 0,  1],
           [-2, -3]])
def fun(y, t):
    yp = dot(A, y)
    return yp

y = odeint(fun, y0, t)

figure(figsize=(7,4))
plot(t, exp(-t) + exp(-2*t), '-', label = 'exact')
plot(t, y[:,0], '.', label = 'odeint')
xlabel('t')
ylabel('y')
legend()
grid(True)

_images/RT_Laplacetransformation_34_0.png

Aufgabe 7: RL-Schaltkreis mit Ramplenspannung¶

An eine Spule mit dem ohmschen Widerstand \(R\) und der Induktivität \(L\) (Serienschaltung) wird zum Zeitpunkt \(t=0\) durch Schließen eines Schalters eine mit der Zeit \(t\) linear ansteigende Spannung \(u(t) = kt\) für \(t \geq 0\) angelegt. Bestimmen Sie mit Hilfe der Laplacetransformation den zeitlichen Verlauf der Stromstärke \(i\) für \(t \geq 0\) , wenn der Stromkreis zu Beginn bei \(t =0\) stromlos ist.

Quelle: Papula: Anwendungsbeispiele, XII, Laplace-Transformationen, Beispiel 3, p. 422ff.

Lösung: Papula: Anwendungsbeispiele, XII, Laplace-Transformationen, Beispiel 3, p. 422ff.: \(i(t) = \frac{kL}{R^2}(e^{-\frac{R}{L}t} + \frac{R}{L}t - 1)\)

Aufgabe 8: GDGL im Frequenzbereich¶

Lösen Sie die GDGL \(\ddot{y}(t) + \dot{y}(t) = e^{-2t}\) mit Anfangsbedingungen \(y(0)=0\) und \(\dot{y}(0)=1\) mittels Laplacetransformation.

Quelle: Papula, Band 2, VI Laplace-Transformation, Abschnitt 5, Aufgabe 9 c), p. 687

Lösung: Papula, Band 2, VI, p. 808. \(y(t) = \frac{1}{2}e^{-2t} - 2e^{-t} + \frac{3}{2}\)

Aufgabe 9: System von GDGL im Frequenzbereich¶

Lösen Sie das folgende nicht-homogene, lineare GDGL-System mittels Laplace-Transformation.

\[\begin{split} \begin{align*} \dot{y}(t) & = - z(t) + t, & \quad y(0) = 1 \\ \dot{z}(t) & = - 4 y(t) , & \quad z(0) = -1 \end{align*} \end{split}\]

Quelle: Bronson: Differential Equations. 4. Auflage, Aufgabe 25.2, S. 250.

Lösung:

\[\begin{split} \begin{align*} y(t) & = -\frac{1}{4} + \frac{7}{8}e^{2t} + \frac{3}{8}e^{-2t} \\ z(t) & = t - \frac{7}{4}e^{2t} + \frac{3}{4}e^{-2t} \end{align*} \end{split}\]

Aufgabe 10: System von GDGL im Frequenzbereich¶

Lösen Sie das folgende nicht-homogene lineare GDGL-System mittels Laplace-Transformation.

\[\begin{split} \begin{align*} \dot{x_1}(t) & = -2 x_1(t) + x_2(t) + 1, & \quad x_1(0) = 0 \\ \dot{x_2}(t) & = x_1(t) - 2 x_2(t), & \quad x_2(0) = 1 \end{align*} \end{split}\]

Quelle: Farlow, An Introduction to Differential Equations and their applications. p. 369

Lösung:

\[\begin{split} \begin{align*} x_1(t) &= \mathcal{L}^{-1}\left(\frac{2}{s(s + 3)}\right) = \mathcal{L}^{-1}\left(\frac{2}{3s} - \frac{2}{3(s + 3)}\right) = \frac{2}{3} - \frac{2}{3}e^{-3t} \\ x_2(t) &= \mathcal{L}^{-1}\left(\frac{s + 1}{s(s + 3)}\right) = \mathcal{L}^{-1}\left(\frac{1}{3s} + \frac{2}{3(s + 3)}\right) = \frac{1}{3} + \frac{2}{3}e^{-3t} \end{align*} \end{split}\]

Aufgabe 11: GDGL im Frequenzbereich mit Anfangsbedingungen, Übertragungsfunktion¶

Lösen Sie \(\ddot{y} - \dot{y} - 2y = 0\) mit Anfangsbedingungen \(y(0)=1\) und \(\dot{y}(0)= 4\) mittels Laplace-Transformation.
Wie lautet die GDGL zur Übertragungsfunktion \(G(s) = \dfrac{10}{(s + 7)(s + 8)}\)?

Quellen:

Vereinfachung von Bronson: Differential Equations. 4. Auflage, 2014, p. 244, Problem 24.6
Nise: Control Systems Engineering. p. 94., problem 8b.

Lösungen:

\(x(t) = \frac{5}{3}e^{2t} - \frac{2}{3}e^{-t}\)
\(\ddot{c}(t) + 15\dot{c}(t) + 56c(t) =10r(t)\)

Aufgabe 12: Anfangswertproblem, Übertragungsfunktion¶

Lösen Sie die GDGL \(y''(t) + 2y'(t) + y(t) = 9e^{2t}\) mit Anfangsbedingungen \(y(0)=0\) und \(y'(0)=1\) mittels Laplacetransformation.
Wie lautet die GDGL zur Übertragungsfunktion \(G(s) = \dfrac{s + 2}{s^3 + 8s^2 + 9s + 15}\)?

Quellen:

Papula, Band 2, VI, 5, p. 669f.
Nise, Chapter 2, problem 8c

Lösungen:

\(-(2t+1)e^{-t} + e^{2t}\)
\(c''' + 8c'' + 9c' + 15c = r' + 2r\)

Aufgabe 13: Laplacetransformation¶

Bestimmen Sie die inverse Laplacetransformierte von \(\dfrac{s + 3}{s^2 - s -2}\).
Lösen Sie das folgende nicht-homogene, lineare GDGL-System mittels Laplace-Transformation.

\[\begin{split}\begin{eqnarray*} \ddot{y}(t) + y(t) + z(t) & = 0, & \quad y(0) = 0,\quad \dot{y}(0) = 0 \\ \dot{z}(t) + \dot{y}(t) & = 0, & \quad z(0) = 1 \end{eqnarray*}\end{split}\]

Quellen:

Bronson: Differential Equations. 4. Auflage, Aufgabe 22.13, S. 229.
Bronson: Differential Equations. 4. Auflage, Aufgabe 25.4, S. 251.

Lösungen:

\(\frac{5}{3}e^{2t} - \frac{2}{3}e^{-t}\)
\begin{align*}y(t) & = -\frac{1}{2}t^2 \ z(t) & = 1 + \frac{1}{2}t^2\end{align*}

Technische Mathematik

Laplacetransformation

Contents

Laplacetransformation¶

Literatur¶

Theorie - Zusammenfassung¶

Idee¶

Definition¶

Eigenschaften¶

Korrespondenztabellen¶

Partialbruchzerlegung¶

Anwendungen¶

Computer¶

Aufgaben¶

Aufgabe 1: GDGL mit Laplacetrafo¶

Aufgabe 2: GDGL System mit Laplacetrafo¶

Aufgabe 3: Übertragungsfunktion, Sprungantwort¶

Aufgabe 4: Übertragungsfunktion und DGL¶

Aufgabe 5: RLC-Schaltungen und Impedanzen¶

Aufgabe 6: Zeit- und Frequenzbereich¶

Aufgabe 7: RL-Schaltkreis mit Ramplenspannung¶

Aufgabe 8: GDGL im Frequenzbereich¶

Aufgabe 9: System von GDGL im Frequenzbereich¶

Aufgabe 10: System von GDGL im Frequenzbereich¶

Aufgabe 11: GDGL im Frequenzbereich mit Anfangsbedingungen, Übertragungsfunktion¶

Aufgabe 12: Anfangswertproblem, Übertragungsfunktion¶

Aufgabe 13: Laplacetransformation¶