Numerik
Contents
Numerik¶
%pylab inline
%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib
# set default values for plotting:
rcParams['axes.titlesize'] = 14
rcParams['axes.labelsize'] = 14
rcParams['xtick.labelsize'] = 14
rcParams['ytick.labelsize'] = 14
rcParams['legend.fontsize'] = 12
rcParams['lines.linewidth'] = 2
Literatur¶
MacCluer: Chapter 12 Divided Differences, p23ff.
Papula: Band 2, IV, 6 Numerische Integration einer DGL, p.472ff.
Bronson, Costa: Chapters 18 and 19
Beispiel: GDGL 1. Ordnung in 1 Dimension¶
Problem: Gegeben die Funktion \(f\) und der Anfangswert \(y_0\) löse
\[y'(x) = f(x,y(x)), y(0)= y_0\]numerisch.
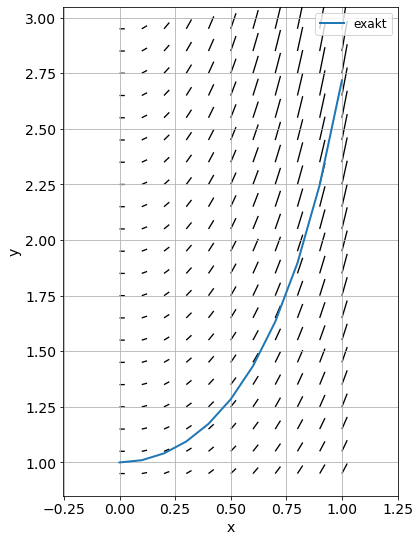
Geometrie: \(f(x,y)\) definiert ein Richtungs-/Steigungsfeld in der \(x\)-\(y\)-Ebene. Finde jene Kurve \(y(x)\), die bei \((x_0,y_0)\) beginnt und Steigungen hat, die gleich den durch \(f\) vorgegebenen sind.
Methode nach Euler¶
Wähle eine Schrittweite \(h>0\) und ersetze \(y'(x)\) durch den Differenzenquotient \(\frac{y(x + h) - y(x)}{h}\). Daraus ergeben sich die folgenden Rekursionen für \(n=0,1,2,3,\ldots\):
Verbesserte Euler-Methode, Heun-Methode¶
Runge-Kutta-Methode¶
Der empfohlene Algorithmus:
Aufgaben¶
Aufgabe 1: GDLG 1. Ordnung¶
Die GDGL 1. Ordnung \(y'(x) = 2xy\) mit Anfangswert \(y(0) = 1\) hat die exakte Lösung \(y(x) = e^{x^2}\). Implementieren Sie die Methoden von Euler und Heun für eine frei wählbare Schrittweite, und vergleichen Sie diese numerischen Lösungen mit der exakten Lösung im Bereich \(x\in[0,1]\).
Lösung:
x = arange(0.00, 1.1, 0.1)
y = arange(0.95, 3.0, 0.1)
X, Y = meshgrid(x, y)
U = ones(X.shape)
V = 2*X*Y
figure(figsize=(6,9))
quiver(X, Y, U, V, headwidth=0.0, headlength=0.01, headaxislength=0.0)
plot(x, exp(x**2), label='exakt')
xlabel('x')
ylabel('y')
axis('equal')
legend()
grid(True)
# Euler-Methode
x0 = 0
y0 = 1
N = 5 # Anzahl Schritte
h = 1/N # Schrittweite
x = zeros(N + 1)
y = zeros(N + 1)
x[0]= x0
y[0]= y0
def my_f(x, y):
return 2*x*y
for n in arange(N):
y[n+1] = y[n] + h*my_f(x[n], y[n])
x[n+1] = x[n] + h
y_Euler = y.copy()
# verbesserte Euler-Methode, Heun-Methode
for n in arange(N):
k = my_f(x[n],y[n])
m = my_f(x[n] + h, y[n] + h*k)
y[n+1] = y[n] + h*(k + m)/2
x[n+1] = x[n] + h
y_Heun = y.copy()
figure(figsize=(6,9))
quiver(X, Y, U, V, headwidth=0.0, headlength=0.01, headaxislength=0.0)
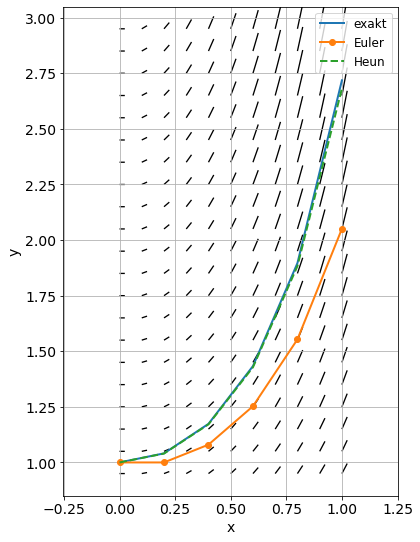
plot(x, exp(x**2), label='exakt', linewidth= 2)
plot(x, y_Euler,'-o', label='Euler', linewidth= 2)
plot(x, y_Heun ,'--', label='Heun', linewidth= 2)
xlabel('x')
ylabel('y')
axis('equal');
legend(numpoints=1)
grid(True)
Aufgabe 2: Räuber-Beute-System¶
Quellen:
MacCluer: Chapter 12 Divided Differences, p. 234f.
Lotka-Volterra-Gleichung:
\(x\) ist die Anzahl der Beutetiere (beispielsweise Kaninchen)
\(y\) ist die Anzahl der Raubtiere (beispielsweise Füchse)
\(\dot{x}\) und \(\dot{y}\) sind die Wachstumsraten der beiden Populationen im Laufe der Zeit
\(a\), \(b\), \(c\) und \(d\) sind Parameter, die die Wechselwirkung der beiden Arten beschreiben
Die exakten Lösungen sind geschlossene Kurven!
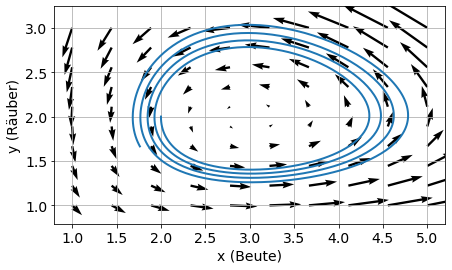
Lösen Sie die DGL mit der Euler-Methode für die Zeiten \(t\in[0,20]\) mit den Parametern \(a = 1,0\), \(b = 0,5\), \(c = 0,75\), \(d = 0,25\) und frei wählbaren Schrittweiten und Anfangszuständen. Stellen Sie das zugehörige Vektorfeld und die Lösung grafisch dar.
Lösung:
a = 1.0
b = 0.5
c = 0.75
d = 0.25
T = 30.0 # Löse von Zeit 0 bis T
N = 1000 # Anzahl Schritte
h = T/N # Schrittweite
t0 = 0
x0 = 2
y0 = 2
s = zeros((2, N)) # matrix of state vectors
s[:,[0]] = array([[x0],
[y0]])
t = zeros(N)
t[0] = t0
def vf(x,y):
xd = a*x - b*x*y
yd = -c*y + d*x*y
return array([[xd],
[yd]])
for n in arange(N-1):
s[:,[n+1]] = s[:,[n]] + h*vf(s[0,n], s[1,n])
t[n+1] = t[n] + h
x = linspace(1, 5, 10)
y = linspace(1, 3, 10)
X, Y = meshgrid(x, y)
figure(figsize=(7,4))
quiver(X, Y, a*X - b*X*Y, -c*Y + d*X*Y)
plot(s[0,:], s[1,:])
axis('equal')
xlabel('x (Beute)')
ylabel('y (Räuber)')
grid(True)
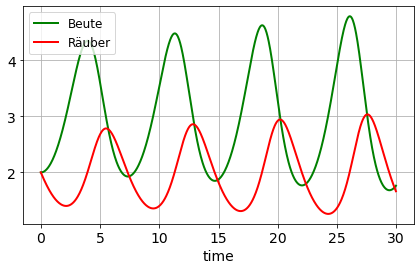
figure(figsize=(7,4))
plot(t, s[0,:], color='green', label='Beute')
plot(t, s[1,:], color='red', label='Räuber')
xlabel('time')
legend(loc='best')
grid(True)
Aufgabe 3: Vergleich numerischer Lösungsmethoden¶
Solververgleich:
Implementieren Sie die Methode von Runge-Kutta für GDGL.
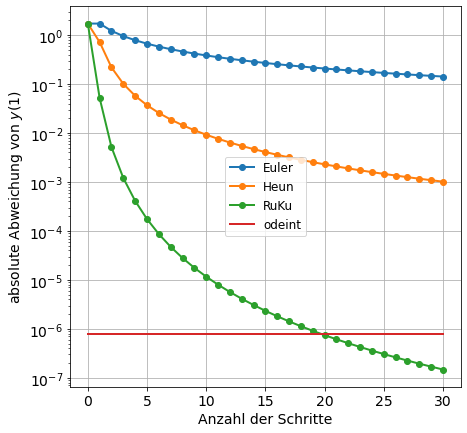
Vergleichen Sie deren Performance mit jenen der Methoden von Euler und Heun am Beispiel der GDGL \(y'(x) = 2xy\) mit Anfangswert \(y(0) = 1\). Erstellen Sie dazu einen Plot, der auf der Abszisse unterschiedliche Anzahlen von verwendeten Schritten \(N\) und auf der Ordinate die zugehörige logarithmische absolute Abweichung \(\log(|y(1) - \hat{y}(1)|)\) des Endwertes der numerischen Berechnung \(\hat{y}(1)\) vom exakten Endwert \(y(1)\) für alle drei Methoden angibt.
Vergleichen Sie zusätzlich die Performance des Solvers odeint.
Lösung:
from scipy.integrate import odeint
x0 = 0
y0 = 1
def my_f(x, y):
return 2*x*y
def my_f_(y, x):
return 2*x*y
N_max = 30 # maximale Anzahl Schritte
N_ = arange(N_max + 1)
y_Euler = zeros(N_max +1)
y_Heun = zeros(N_max +1)
y_RuKu = zeros(N_max +1)
y_Euler[0] = y0
y_Heun[0] = y0
y_RuKu[0] = y0
for N in arange(1, N_max + 1): # Anzahl Schritte
h = 1/N # Schrittweite
x = zeros(N + 1)
y = zeros(N + 1)
x[0]= x0
y[0]= y0
# Euler:
for n in arange(N):
y[n+1] = y[n] + h*my_f(x[n], y[n])
x[n+1] = x[n] + h
y_Euler[N] = y[-1]
# Heun:
for n in arange(N):
k = my_f(x[n],y[n])
m = my_f(x[n] + h, y[n] + h*k)
y[n+1] = y[n] + h*(k + m)/2
x[n+1] = x[n] + h
y_Heun[N] = y[-1]
# Runge-Kutta:
for n in arange(N):
k1 = my_f(x[n],y[n])
k2 = my_f(x[n] + h/2, y[n] + h*k1/2)
k3 = my_f(x[n] + h/2, y[n] + h*k2/2)
k4 = my_f(x[n] + h , y[n] + h*k3)
y[n+1] = y[n] + h/6*(k1 + 2*k2 + 2*k3 + k4)
x[n+1] = x[n] + h
y_RuKu[N] = y[-1]
# odeint
y = odeint(my_f_, y0, x)
y_odeint = y[-1]
figure(figsize=(7,7))
semilogy(N_, abs(e - y_Euler) ,'o-', label='Euler')
semilogy(N_, abs(e - y_Heun) ,'o-', label='Heun')
semilogy(N_, abs(e - y_RuKu) ,'o-', label='RuKu')
semilogy(N_, ones(shape(N_))*abs(e - y_odeint),'-', label='odeint')
xlabel('Anzahl der Schritte')
ylabel('absolute Abweichung von $y(1)$')
legend(numpoints=1)
grid(True)