Anwendungen¶

%pylab inline

%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib

# set default values for plotting:
rcParams['axes.titlesize']  = 14
rcParams['axes.labelsize']  = 14
rcParams['xtick.labelsize'] = 14
rcParams['ytick.labelsize'] = 14
rcParams['legend.fontsize'] = 12
rcParams['lines.linewidth'] = 2

Literatur¶

Schulz: Regelungstechnik 1
Philippsen: Einstieg in die Regelungstechnik
Jörgl: Repetitorium Regelungstechnik - Band 1
Haager: Regelungstechnik
Nise: Control Systems Engineering, Chapter 2 Modeling in the Frequency Domain
Papula: Band 2, VI, Laplace-Transformationen

Theorie - Zusammenfassung¶

Anfangs- und Endwertsatz¶

\[\begin{split} \begin{align*} \lim_{t \to 0}f(t) &= \lim_{s \to \infty}sF(s) \\ \lim_{t \to \infty}f(t) &= \lim_{s \to 0}sF(s) \end{align*} \end{split}\]

Rechnen mit Übertragungsfunktionen¶

Reihenschaltung: \(G(s) = G_1(s)G_2(s)\)
Parallelschaltung: \(G(s) = G_1(s) + G_2(s)\)
Rückkopplung: \(G(s) = \dfrac{G_1(s)}{1 + G_1(s)G_2(s)}\)

Frequenzgang¶

Der komplexe Verstärkungsfaktor eines harmonischen Inputs ist

\[G(j\omega) = |G(j\omega)|e^{j\varphi(\omega)}\]

mit \(\varphi\) dem Argument (Winkel, Phase) von \(G(j\omega))\).

Ortskurve: \(G(j\omega)\) in der komplexen Zahlenebene
Amplitudengang: \(|G(j\omega)|\)
Phasengang: \(\text{arg }G(j\omega)\)

Stabilität¶

Stabilität: Bei konstaten Eingangsgrößen muss der Ausgang auf einen konstanten Wert abklingen.

Damit ein System, das durch die Übertragungsfunktion

\[G(s) = \frac{b_m s^m + b_{m-1} s^{m-1} + + b_1 s + b_0}{s^n + a_{n-1} s^{n-1} + + a_1 s + a_0}\]

gegeben ist, stabil ist, müssen alle Nullstellen des Nennerpolynoms einen negativen Realanteil aufweisen. Alle Polstellen der Übertragungsfunktion müssen also in der linken Halbebene der komplexen Zahlenebene liegen.

Nyquistkriterium:

Das Nyquistkriterium liefert eine Aussage über die Stabilität des geschlossenen Regelkreises

\[G_g(s) = \frac{G_o(s)}{1 + G_o(s)}\]

aus dem Frequenzgang der offenen Systems \(G_o(s)\).

Man befindet sich an der Stabilitätsgrenze (imaginäre Achse), wenn

\[\begin{split} \begin{align*} 1 + G_o(s) & = 0 \quad \text{hat eine imaginäre Lösung } j\omega_1 \\ G_o(j\omega_1) & = -1 \end{align*} \end{split}\]

Wenn sich also der gechlossene Regelkreis an der Stabilitätsgrenze befindet, dann verläuft die Ortskurve des offenen Systems \(G_o(s)\) bei einer bestimmten Frequenz \(\omega_1\) durch den Punkt \((-1,0)\), den sogenannten Nyquistpunkt. Es gilt:

Verläuft die Ortskurve des offenen Systems \(G_o(s)\) in Richtung steigender \(\omega\)-Werte so, dass der Nyquistpunkt auf der linken Seite liegt, dann ist der geschlossene Regelkreis \(G_g(s)\) stabil.
Verläuft die Ortskurve des offenen Systems \(G_o(s)\) in Richtung steigender \(\omega\)-Werte so, dass der Nyquistpunkt auf der rechten Seite liegt, dann ist der geschlossene Regelkreis \(G_g(s)\) instabil.

Literatur: Philippsen, p. 142ff, Haager, p. 109, Schulz, Jörgl, Nise

Anwendungen¶

Regelungstechnik: Regler, Frequenzgang, Stabilität etc.

Aufgaben¶

Aufgabe 1: Endwertsatz¶

Eines System hat die Übertragungsfunktion \(G(s)= \frac{1}{s + 2}\). Bestimmen Sie mit dem Endwertsatz den Endwert der Sprungantwort.

Lösung: \(\frac{1}{2}\)

Aufgabe 2: Anfangs- und Endwertsatz¶

Bestimmen Sie das Verhalten von \(x(t)\) für \(t\rightarrow 0\) und \(t\rightarrow \infty\), wenn die Lapalacetransformierte \(X(s)\) von \(x(t)\) folgende Ausdrücke hat:

\(X(s) = \dfrac{6(s+2)}{(s+1)(s+3)(s+4)}\)
\(X(s) = \dfrac{s^2+2s+2}{s(s+1)^3(s+2)}\)
\(X(s) = \dfrac{32}{s^2(s+2)(s+4)}\)

Quelle: Jörgl: Repetitorium Regelungstechnik - Band 1. 2. Auflage, Oldenbourg, 1995. Aufgabe 4.8., p. 37.

Lösung:

\(\lim_{t\to 0}x(t) = 0\), \(\lim_{t\to \infty}x(t) = 0\)
\(\lim_{t\to 0}x(t) = 0\), \(\lim_{t\to \infty}x(t) = 1\)
\(\lim_{t\to 0}x(t) = 0\), \(\lim_{t\to \infty}x(t) = \infty\)

Aufgabe 3: Anfangs- und Endwertsatz¶

Bestimmen Sie das Verhalten von \(x(t)\) für \(t\rightarrow 0\) und \(t\rightarrow \infty\), wenn die Lapalacetransformierte \(X(s)\) von \(x(t)\) folgenden Ausdruck hat: \(X(s) = \dfrac{4(s+3)}{s(s+6)}\).

Quelle: Jörgl: Repetitorium Regelungstechnik - Band 1. 2. Auflage, Oldenbourg, 1995. Aufgabe 4.8.d), p. 37.

Lösung: \(\lim_{t\to 0}x(t)=4\), \(\lim_{t\to \infty}x(t)=2\)

Aufgabe 4: Anfangs- und Endwertsatz¶

Ermitteln Sie für folgende Übertragungsfunktionen mit Hilfe des Anfangs- und Endwertsatzes die Anfangs- und Endwerte der jeweiligen Sprunganwort.

(a) \(G(s) = \dfrac{1}{(s + 1)(s + 2)}\),\(\;\) (b) \(G(s) = \dfrac{s(s + 1)}{s + 2}\),\(\;\) (c) \(G(s) = \dfrac{s + 1}{s + 1}\),\(\;\) (d) \(G(s) = \dfrac{1 + 10s}{1 + 2s}\)

Quelle: vgl. Haager p. 18 und p. 150

Lösung: (a) AW = \(0\) und EW = \(0,5\), (b) AW = \(\infty\) und EW = \(0\), (c) AW = \(1\) und EW = \(1\), (d) AW = \(5\) und EW = \(1\)

Aufgabe 5: Blockschaltbild, Übertragungsfunktion¶

Bestimmen Sie die Übertragungsfunktion des folgenden Blockschaltbilds.

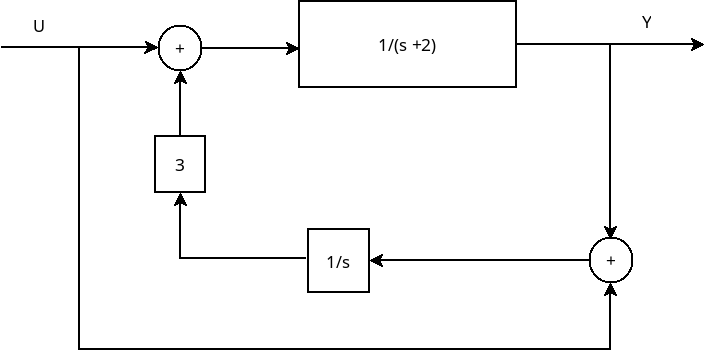
System_1

Quelle: Jörgl: Repetitorium Regelungstechnik - Band 1. 2. Auflage, Oldenbourg, 1995. Aufgabe 5.5, p. 52.

Lösung: \(G(s) = \dfrac{1}{s-1}\)

Aufgabe 6: Blockschaltbild, Übertragungsfunktion¶

Bestimmen Sie die Führungsübertragungsfunktion \(G_W(s)\) und die Störübertragungsfunktion \(G_Z(s)\) des folgenden Blockschaltbilds.

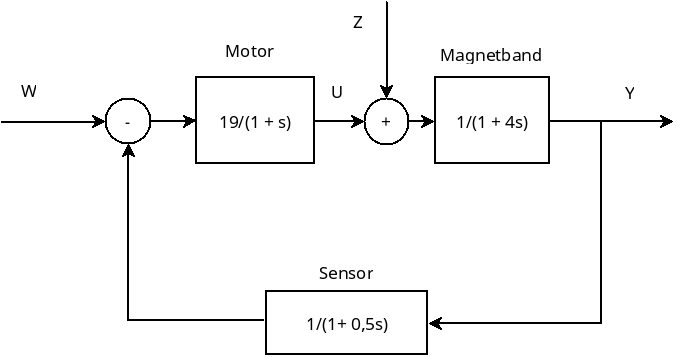
System_2

Hinweis: \(Y(s) = G_W(s) W(s) + G_Z(s) Z(s)\)

Quelle: Jörgl: Repetitorium Regelungstechnik - Band 1. 2. Auflage, Oldenbourg, 1995. Aufgabe 5.7, p. 53.

Lösung:

\(G_W(s) = \frac{19(1 + 0,5s)}{2s^3 + 6,5s^2 + 5,5s + 20}\), \(G_Z(s) = \frac{(1 + s)(1 + 0,5s)}{2s^3 + 6,5s^2 + 5,5s + 20}\)

Aufgabe 7: Frequenzgang¶

Plotten Sie den Frequenzgang eines RC-Spannungsteilers: Input = Spannung an R und C, Output = Spannung an C

Lösung:

R = 1
C = 1
omega = linspace(0, 1000, 10000) # rad/sec
G = 1/( 1 + (omega*R*C)*1j )

figure(figsize=(6,6))
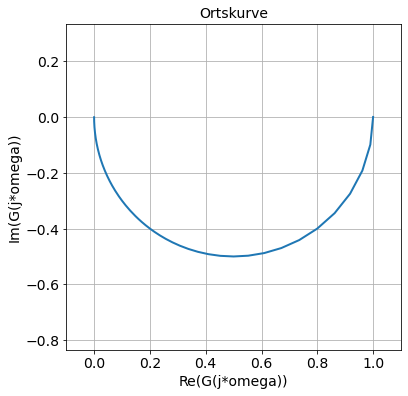
plot(G.real, G.imag, '-')
title('Ortskurve')
xlabel('Re(G(j*omega))')
ylabel('Im(G(j*omega))')
axis('equal')
xlim(-0.1, 1.1)
grid(True)

figure(figsize=(6,6))
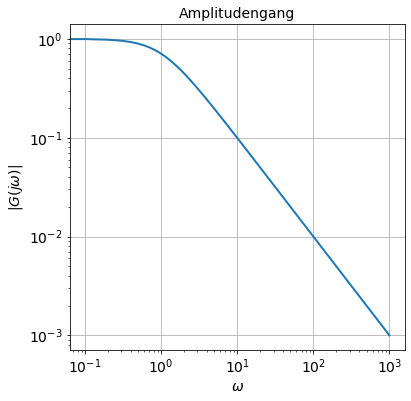
loglog(omega, absolute(G))
xlabel('$\omega$')
ylabel('$|G(j\omega)|$')
title('Amplitudengang')
grid(True)

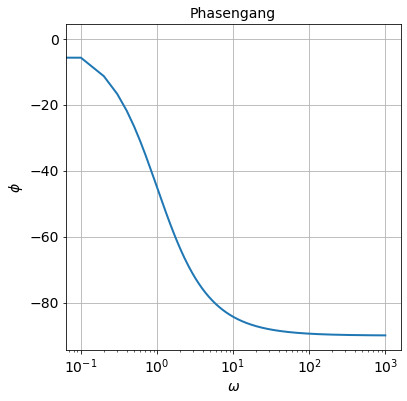
figure(figsize=(6,6))
semilogx(omega, angle(G, deg = True))
xlabel('$\omega$')
ylabel('$\phi$')
title('Phasengang')
grid(True)

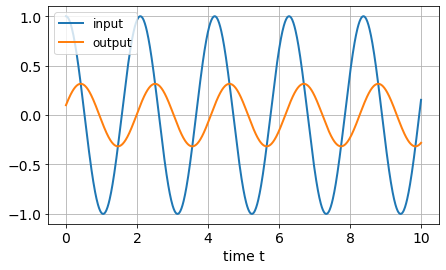
omega = 3
t = linspace(0, 10, 1000)
r = exp(1j*omega*t) # complex input
G = 1/( 1 + (omega*R*C)*1j )
c = G*r # complex output

figure(figsize=(7,4))
plot(t, r.real, label='input')
plot(t, c.real, label='output')
xlabel('time t')
legend()
grid(True)

Aufgabe 8: Frequenzgang¶

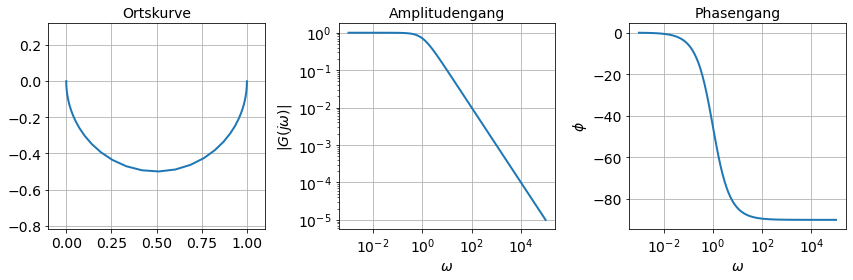
Skizzieren Sie ohne Computer von Hand den Frequenzgang der Übertragungsfunktion \(G(s)=\dfrac{1}{1 + s}\), d. h.

Orstkurve
Amplitudengang
Phasengang

Lösung:

omega = logspace(-3, 5, 100) # rad/sec
G = 1/(1 + omega*1j)

figure(figsize=(12, 4))
#fig.set_size_inches(14, 4)

subplot(1,3,1)
plot(G.real, G.imag, '-')
axis('equal')
xlim(-0.1, 1.1)
title('Ortskurve')
grid(True)

subplot(1,3,2)
loglog(omega, absolute(G), '-')
xlabel('$\omega$')
ylabel('$|G(j\omega)|$')
title('Amplitudengang')
grid(True)

subplot(1,3,3)
semilogx(omega, angle(G, deg = True), '-')
xlabel('$\omega$')
ylabel('$\phi$')
title('Phasengang')
grid(True)

tight_layout()

Aufgabe 9: Frequenzgang, Ortskurve¶

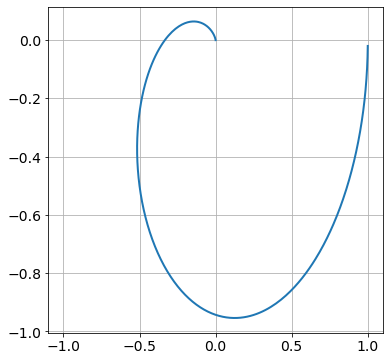
Plotten Sie die Orstkurve der Übertragungsfunktion \(G(s) = \dfrac{1}{(1 + s)(1 + s + s^2)}\).
Bei welcher Kreisfrequenz \(\omega_1\) schneidet die Orstkurve die relle Achse? Wie groß ist dabei die Amplitudenverstärkung?

Quelle: Haager p. 41 und p. 151

Lösung:

Siehe Code
\(\text{Im}(G(j\omega)) = \dfrac{\omega^3 - 2\omega}{(1 + \omega^2)( (1-\omega^2)^2 + \omega^2 )}\), \(\omega_1 = \sqrt{2}\), \(|G(j\omega_1)| = \frac{1}{3}\)

#omega = linspace(0, 1000, 10000) # rad/sec
omega = logspace(-2, 4, 1000) # rad/sec 
G = 1/( (1 + omega*1j)*(1 + omega*1j - omega**2) )

figure(figsize=(6,6))
plot(G.real, G.imag, '-')
xlim(-1.1, 1.1)
grid(True)

omega1 = sqrt(2) # rad/sec
G1 = 1/( (1 + omega1*1j)*(1 + omega1*1j - omega1**2) )
G1

(-0.33333333333333326+7.401486830834373e-17j)

Aufgabe 10: Frequenzgang - allgemeine Schwingung¶

Die allgemeine Schwingungsgleichung lautet

\[\ddot{x}_a(t) + 2\delta \dot{x}_a(t) + \omega_0^2 x_a(t) = x_e(t).\]

Analysieren Sie anhand der Übertragungsfunktion

den Frequenzgang
die Stabilität in Abhängigkeit der Parameter \(\delta\) und \(\omega_0\).

Quelle: Philippsen p. 77 ff.

Verwenden Sie dazu das Python-Paket ipywidgets. Ein Code-Beispiel ist unten angegeben.

from ipywidgets import interact, fixed

def my_plot(k, d):
    figure(figsize=(4,4))
    x = linspace(-2, 5)
    plot(x, k*x + d)
    xlim(-2, 5)
    ylim(-2, 5)
    xlabel('x')
    ylabel('y')
    grid(True)
    show()
    return

interact(my_plot,
         k = (-2.0, 3.0), 
         d = (-1.0, 3.0)
        );

Lösung:

Frequenzgang:

def my_plot(omega_0, delta, plot_type):
    omega = logspace(0, 3, 1000)
    G = 1/( - omega**2 + 2*delta*omega*1j + omega_0**2)
    if plot_type == 'Amplitudengang':
        loglog(omega, absolute(G), '.-')
        xlabel('$\omega$')
        ylabel('$|G(j\omega)|$')
        title('Amplitudengang')
    elif plot_type == 'Phasengang':
        semilogx(omega, angle(G, deg = True), '.-')
        xlabel('$\omega$')
        ylabel('$\phi$')
        title('Phasengang')
    grid(True)
    show()
    return

interact(my_plot, 
         omega_0   = ( 0.0, 100.0), 
         delta     = ( 0.0, 5.0),
         plot_type = ['Amplitudengang', 'Phasengang']
        );

Stabilität: Der Nenner von \(G(s) = \dfrac{1}{s^2 + 2\delta s + \omega_0^2}\) ist Null bei \(s_{1,2} = -\delta \pm \sqrt{\delta^2 - \omega_0^2}\).

def my_plot(omega_0, delta, plot_type):
    omega = logspace(0, 3, 1000)
    if plot_type == 'Polstellen':
        p = [1, 2*delta, omega_0**2]  # p[0] * x**n + p[1] * x**(n-1) + ... + p[n-1]*x + p[n]
        rs = roots(p)
        for r in rs:
            plot(r.real, r.imag, 'ok', label=str(r))
        xlim(-25, 2)
        ylim(-12, 12)
        legend(loc = 'best', numpoints =1)
    elif plot_type == 'Ortskurve':
        G = 1/( - omega**2 + 2*delta*omega*1j + omega_0**2)
        plot(0, 0, 'o')
        plot(G.real, G.imag, '-')
        axis('equal')
    grid(True)
    return

interact(my_plot, 
         omega_0 = (  0.0, 10.0), 
         delta   = ( -1.0, 10.0),
         plot_type = ['Polstellen', 'Ortskurve'],
        );

Aufgabe 11: Stabilität¶

Bestimmen Sie die Stabilität des rückgekoppelten Integrators mit DGL

\[\dot{x_a}(t) = x_e(t) + k x_a(t).\]

Quelle: Philippsen, S. 142 f.

Aufgabe 12: Regelabweichung, Endwerttheorem¶

Die Regelstrecke mit der Übertragungsfunktion \(G(s)=\dfrac{1}{1+5s}\) wird mit dem Regler \(R(s)=k\) geregelt.

Wie ist die Verstärkung zu wählen, damit sich bei einer sprungförmigen Führungsgröße eine stationäre Regelabweichung von 10 % ergibt?

Quelle: Haager: Regelungstechnik. öbv & hpt, 2. Auflage, 2000. Aufgabe 1.2.4-2, p. 56., p. 153.

Lösung:

Übertragungsfunktion von Fehler zu Führungsgröße \(\dfrac{E(s)}{W(s)}=\dfrac{1 + 5s}{1 + 5s + k}\), Endwerttheorem: \(\dfrac{1}{1+k}=0.1\) für \(k=9\).

Aufgabe 13: Nyquistkriterium¶

Gegeben ist ein offenes System bestehend aus einem

Proportionalregler mit Verstärkung \(K\) vor der
Strecke mit Übertragungsfunktion \(\frac{1}{Ts + 1}\).

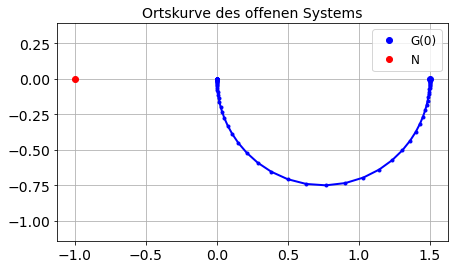
Untersuchen Sie mit dem Nyquistkriterium die Stabilität des geschlossenen Systems, indem Sie die

Ortskurve des offenen Systems und die
Sprungantwort des geschlossenen Systems

bestimmen. Verwenden Sie die Funktionen von SciPy Signal processing: Continuous-Time Linear Systems, um die Ergebnisse der Vorlesung anhand der zeitlichen Verläufe zu überprüfen.

Hinweis: Schauen Sie sich zuerst das Notebook RT_SciPy_Signal.ipynb an.

Quelle: Ogata 4th ed., S. 282 f.

Lösung:

from scipy import signal

# offenes System
K = 1.5
T = 1.0

num = [K]
den = [T, 1]

system_offen = signal.TransferFunction(num, den)

# Ortskurve des offenen Systems
omega = logspace(-3, 5, 100)
omega, G = system_offen.freqresp(omega)

figure(figsize=(7,4))
plot(G.real, G.imag, ".-b")
G0 = K # G(0)
plot(G0.real, G0.imag, "ob", label='G(0)')
N = -1
plot(N.real, N.imag, "or", label='N')
axis('equal')
legend()
title('Ortskurve des offenen Systems')
grid(True)

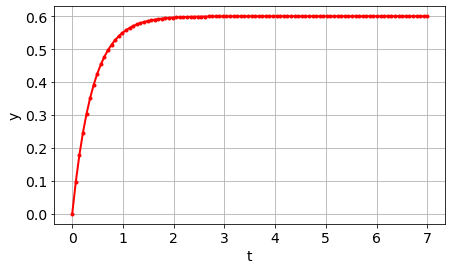
# Sprungantwort des geschlossenen Systems:

num = [K]
den = [T, 1 + K]

system_gesch = signal.TransferFunction(num, den)

t = linspace(0, 7, 100)
x0 = None

figure(figsize=(7,4))
t, y = signal.step(system_gesch, x0, t)
plot(t, y, '.-r')
xlabel('t')
ylabel('y')
grid(True)

Aufgabe 14: Regelungstechnik¶

Bestimmen Sie die Übertragungsfunktion des folgenden Blockschaltbilds.

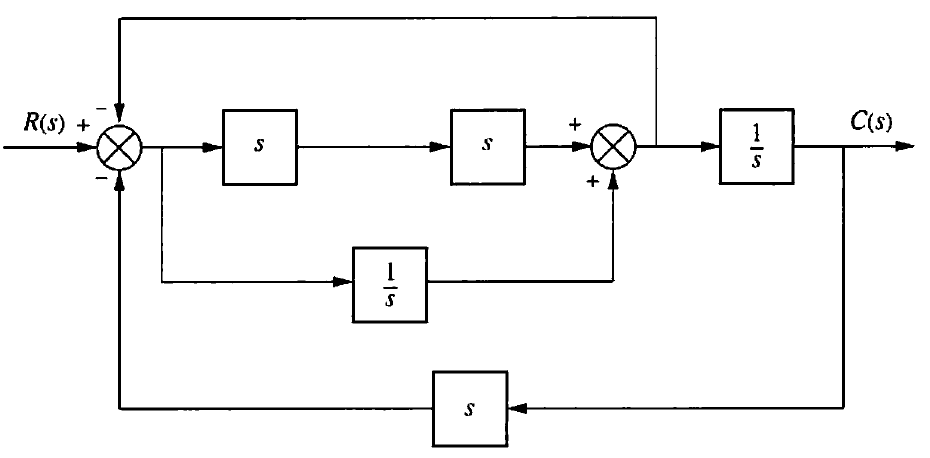
Quelle: Nise 6th ed. Skill-Assessment Exercise 5.1

Lösung:

\(\dfrac{s^3 + 1}{2s^4 + s^2 + 2s}\)

Technische Mathematik

Anwendungen

Contents

Anwendungen¶

Literatur¶

Theorie - Zusammenfassung¶

Anfangs- und Endwertsatz¶

Rechnen mit Übertragungsfunktionen¶

Frequenzgang¶

Stabilität¶

Anwendungen¶

Aufgaben¶

Aufgabe 1: Endwertsatz¶

Aufgabe 2: Anfangs- und Endwertsatz¶

Aufgabe 3: Anfangs- und Endwertsatz¶

Aufgabe 4: Anfangs- und Endwertsatz¶

Aufgabe 5: Blockschaltbild, Übertragungsfunktion¶

Aufgabe 6: Blockschaltbild, Übertragungsfunktion¶

Aufgabe 7: Frequenzgang¶

Aufgabe 8: Frequenzgang¶

Aufgabe 9: Frequenzgang, Ortskurve¶

Aufgabe 10: Frequenzgang - allgemeine Schwingung¶

Aufgabe 11: Stabilität¶

Aufgabe 12: Regelabweichung, Endwerttheorem¶

Aufgabe 13: Nyquistkriterium¶

Aufgabe 14: Regelungstechnik¶