Numerik¶

%pylab inline

from ipywidgets import interact

%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib

# set default values for plotting:
rcParams['axes.titlesize']  = 14
rcParams['axes.labelsize']  = 14
rcParams['xtick.labelsize'] = 14
rcParams['ytick.labelsize'] = 14
rcParams['legend.fontsize'] = 12
rcParams['lines.linewidth'] = 2

Finite Differenzen¶

Literatur:

Farlow, Part 5, Lessons 37, 38
MacCluer, Chapter 12
Logan, Chapter 6, Sections 1 - 3

Crank-Nicolson¶

Literatur:

MacCluer, Chapter 12
Farlow, Part 5, Lesson 39
Logan, Chapter 6, Section 4

Galerkin und Finite Elemente¶

Literatur:

MacCluer, Chapter 13

Aufgabe 1: Laplacegleichung¶

\(u_{xx} + u_{yy}=0\)

\(y\)-Achse \(\downarrow\) mit \(M\) Stützstellen und Index \(m\)
\(x\)-Achse \(\rightarrow\) mit \(N\) Stützstellen und Index \(n\)

M = 40
N = 80

u = zeros((M,N))

case = "electric" # zwei elektrische Ladungen
case = "thermal"  # thermische Randbedingungen

if case == "electric": 
    u[3*M//4,   N//4] = -1
    u[  M//4, 3*N//4] = +1
elif case == "thermal":
    u[:,0]  = 1  # linke Randbedingung
    u[:,-1] = 2  # rechte Randbedingung
    u[0,:]  = 3  # obere Randbedingung
    u[-1,:] = 4  # untere Randbedingung
    
    
def iteration(u):
    for m in range(1, M-1):
        for n in range(1, N-1):
            u[m,n] = 0.25*(u[m+1,n] + u[m-1,n] + u[m,n+1] + u[m,n-1])
            if case == "electric":
                u[3*M//4,   N//4] = -1
                u[  M//4, 3*N//4] = +1
    return u

# u

iterations = 300
for i in range(iterations):
    u = iteration(u)

v = u.copy()
err = iteration(v) - u
abs(err).max()  

0.005600289574479778

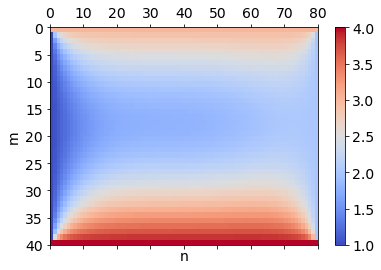
fig, ax = subplots(figsize=(6,4))
cax = ax.matshow(u, extent=(0, N, M, 0), aspect='auto', cmap=cm.coolwarm) 
                  # extent = (left, right, bottom, top)
# alternativer Befehl imshow:    
#cax = ax.imshow(u, extent=(0, N, M, 0), aspect='auto', cmap=cm.coolwarm)    
fig.colorbar(cax)
xlabel('n')
ylabel('m')
grid(False)

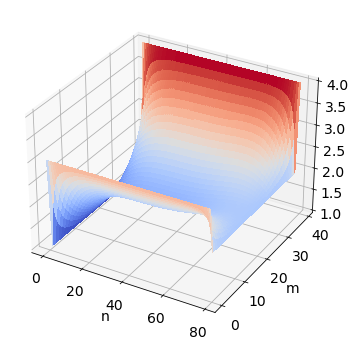
from mpl_toolkits.mplot3d import Axes3D

x = arange(N)
y = np.arange(M)
X, Y = np.meshgrid(x, y)

fig = plt.figure(figsize=(8,6))
ax = fig.gca(projection='3d')
ax.plot_surface(X, Y, u, rstride=1, cstride=1, cmap=cm.coolwarm,
        linewidth=0, antialiased=False)
# ax.view_init(azim = -90,elev = 30)
xlabel('n')
ylabel('m')
grid(False)

/tmp/ipykernel_13818/714610437.py:8: MatplotlibDeprecationWarning: Calling gca() with keyword arguments was deprecated in Matplotlib 3.4. Starting two minor releases later, gca() will take no keyword arguments. The gca() function should only be used to get the current axes, or if no axes exist, create new axes with default keyword arguments. To create a new axes with non-default arguments, use plt.axes() or plt.subplot().
  ax = fig.gca(projection='3d')

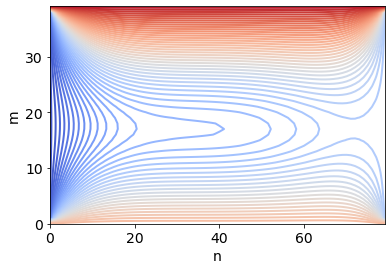
# 50 Konturlinien:
contour(u, 50, cmap=cm.coolwarm) 
xlabel('n')
ylabel('m')
grid(False)

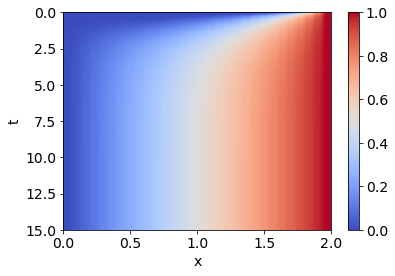
Aufgabe 2: Wärmeleitungsgleichung¶

\(u_t = \alpha u_{xx}\), \(0\leq x \leq L\), \(0\leq t \leq T\),

\(t\)-Achse \(\downarrow\) mit Schrittweite \(k\) und Index \(m\), \(M\) Stützstellen
\(x\)-Achse \(\rightarrow\) mit Schrittweite \(h\) und Index \(n\), \(N\) Stützstellen

Aufgaben:

Implementieren Sie eine explizite numerische Lösung.
Überprüfen Sie durch Variationen der Parameter die Stabilitätsbedingung \(\frac{\alpha k}{h^2} \leq \frac{1}{2}\).
Implementieren Sie zeitlich variierende Randbedingungen.
Implementieren Sie einen Wärmetransfer am rechten Ende.

a = 0.3   # alpha der Wärmeleitungsgleichung
T = 15    # zeitliche Spanne
L = 2     # räumliche Spanne

M = 5000  # Anzahl Stützstellen für Zeit
N = 30    # Anzahl Stützstellen für Raum

k = T/(M - 1)  # Schrittweite für Zeit
h = L/(N - 1)  # Schrittweite für Raum

print("Stabilitätsbedingung:", a*k/h**2)

t = linspace(0, T, M)
x = linspace(0, L, N)

# u(t, x):
u = zeros((M, N)) # Initalisierungmit Nullen
u[0,:] = 0       # Anfangsbedingung für t=0

# linke Randbedingung bei x=0 für alle Zeiten:
u[:,0] = 0      
# u[:,0] = linspace(1,0,M)

# rechte Randbedingung bei x=L für alle Zeiten:
u[:,-1] = 1
# u[:,-1] = sin(t)

# Kontakt-Aussentemperatur rechts bei x=L:
lbd = 1
g = 1*ones_like(t)
g = 1*sin(t)
#g = t/T

# u

Stabilitätsbedingung: 0.1892628525705141

for m in range(0, M-1):
    for n in range(1,N-1):
        u[m+1,n] = u[m,n] + a*k/h**2*(u[m,n-1] - 2*u[m,n] + u[m,n+1])
        # for contact temperature include:
        # u[m+1,N-1] = (u[m+1,N-2] + h*lbd*g[m+1])/(1 + h*lbd)

fig, ax = subplots(figsize=(6,4))
cax = ax.imshow(u, extent=(0, L, T, 0), aspect='auto', cmap=cm.coolwarm) 
                 # extent = (left, right, bottom, top)
fig.colorbar(cax)
xlabel('x')
ylabel('t')
grid(False)

# Interaktive Darstellung: 
# https://github.com/ipython/ipywidgets
# Evtl. jupyter nbextension enable --py --sys-prefix widgetsnbextension im Command Window ausführen.

def my_f(t):
    figure(figsize=(6,3))
    m = t/k  # t = m*k
    m = int(m)
    plot(x, u[m,:],'.-')
    xlabel('x')
    xlim((0, L))
    ylim((-1.2, 1.2))
    grid(True)

interact(my_f, t=(0, T, k));

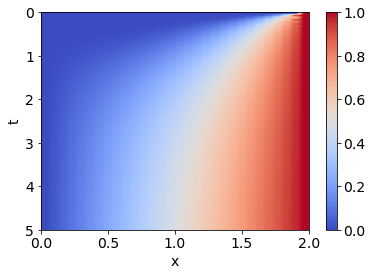
Aufgabe 3: Crank-Nicolson, Wärmeleitungsgleichung¶

Literatur: MacCluer, Chapter 12, 238 ff.

a = 0.3   # alpha 
T = 5
L = 2

M = 100
N = 30

k = T/(M-1)
h = L/(N-1)

r = a*k/h**2
print("r =", r)

u = zeros((M, N))
u[0,:]  = 0    # Anfangsbedingung
u[:,0]  = 0    # linke Randbedingung
u[:,-1] = 1    # rechte Randbedingung

r = 3.1856060606060606

v = concatenate(([0], ones(N - 2)))
w = concatenate((ones(N - 2), [0]))
d = concatenate(([0], ones(N - 2), [0]))

R = -2*diag(d) + diag(v, 1) + diag(w, -1)
I = eye(N, N)

A = I - r/2*R
for m in range(0, M-1):
    b = dot(I + r/2*R, u[m,:])
    u[m + 1,:] = solve(A, b)

fig, ax = subplots(figsize=(6,4))
cax = ax.imshow(u, extent=(0, L, T, 0), aspect='auto', cmap=cm.coolwarm)
# extent = (left, right, bottom, top)
fig.colorbar(cax)
xlabel('x')
ylabel('t')
grid(False)

def my_f(m):
    figure(figsize=(6,3))
    plot(u[m,:],'.-')
    xlabel('n')
    xlim((0, N-1))
    ylim((-1.2, 1.2))            
    grid(True)

interact(my_f, m=(0, M-1, 1)); 

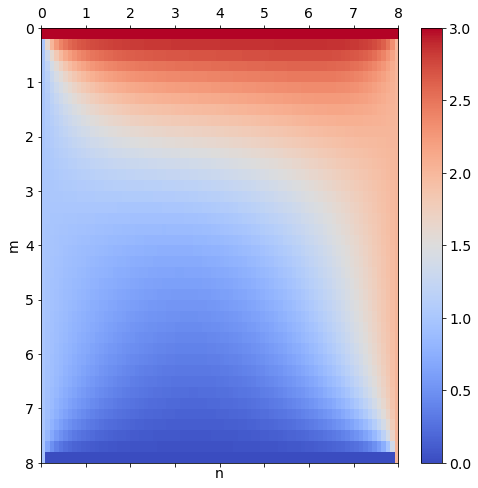
Aufgabe 4: Laplacegleichung¶

Wir betrachten die Laplacegleichung \(u_{xx} + u_{yy}=0\) mit

\(y\)-Achse \(\downarrow\) mit \(M\) Stützstellen, Index \(m\) und Schrittweite \(k\)
\(x\)-Achse \(\rightarrow\) mit \(N\) Stützstellen, Index \(n\) und Schrittweite \(h\)

und interpretieren \(u(x,y)\) als stationäre Temperaturverteilung in einem 2-dimensionalen Raumgebiet.

Implementieren Sie die explizite Methode der finiten Differenzen für unterschiedliche Schrittweiten \(h\) und \(k\).
Lösen Sie damit die Laplacegleichung in einem quadratischen \(x\)-\(y\)-Gebiet mit den folgenden Randbedingungen:
- am linken Rand ist \(u\) immer gleich 1
- am rechten Rand ist \(u\) immer gleich 2
- am oberen Rand ist \(u\) immer gleich 3
- am unteren Rand ist \(u\) immer gleich 0
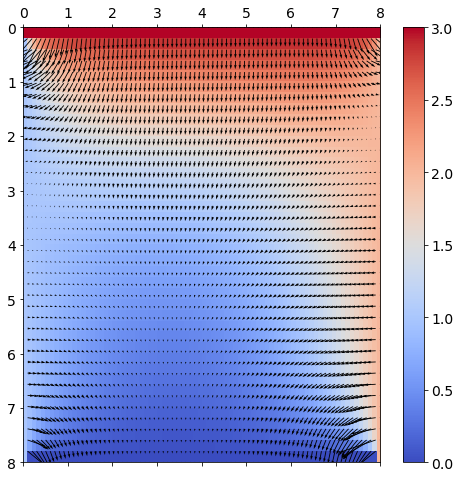
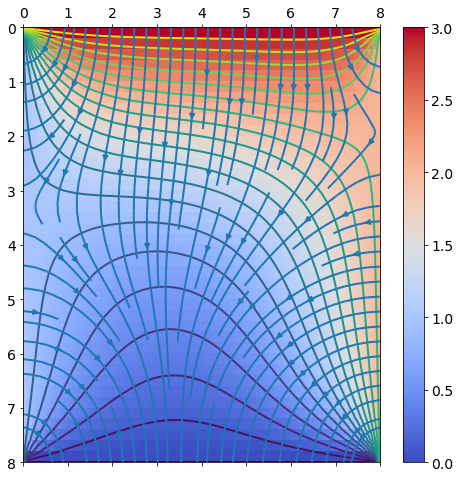
Berechnen Sie mit der central difference approximation den Wärmefluss (unter der Annahme, dass die therm. Konduktivität \(K=1\)) und stellen Sie diesen gemeinsam mit der Temperaturverteilung dar. Hinweis: Verwenden Sie für die Darstellung des Wärmeflusses die Funktion quiver oder die Funktion streamplot.

Lösung:

M = 40
N = 80

h = 0.1
k = 0.2
x = linspace(0, N*h, N)
y = linspace(0, M*k, M)

u = zeros((M, N))

# Randbedingungen:
u[:,0]  = 1  # linke Randbedingung
u[:,-1] = 2  # rechte Randbedingung
u[0,:]  = 3  # obere Randbedingung
#u[-1,:] = 4  # untere Randbedingung

def iteration(u):
    for m in range(1, M-1):
        for n in range(1, N-1):
            u[m,n] = k**2/(2*k**2 + 2*h**2)*(u[m  ,n+1] + u[m  ,n-1]) + \
                     h**2/(2*k**2 + 2*h**2)*(u[m+1,n  ] + u[m-1,n  ])
    return u

iterations = 500
for i in range(iterations):
    u = iteration(u)

v = u.copy()
err = iteration(v) - u
abs(err).max()  

0.0017676432948432463

fig, ax = subplots(figsize=(8,8))
cax = ax.matshow(u, extent=(0, N*h, M*k, 0), aspect='auto', cmap=cm.coolwarm) 
                  # extent = (left, right, bottom, top)
fig.colorbar(cax)
xlabel('n')
ylabel('m')
grid(False)

u_x = zeros((M, N))
u_y = zeros((M, N))

for m in range(1, M-1):
        for n in range(1, N-1):
            u_x[m,n] = 1/(2*h)*( u[m  ,n+1] - u[m  ,n-1] )
            u_y[m,n] = 1/(2*k)*( u[m+1,n  ] - u[m-1,n  ] )

X, Y = np.meshgrid(x, y)

fig, ax = subplots(figsize=(8,8))
cax = ax.matshow(u, extent=(0, N*h, M*k, 0), aspect='auto', cmap=cm.coolwarm) 
fig.colorbar(cax)
quiver(X, Y, -u_x, u_y, scale=30)
grid(False)

fig, ax = subplots(figsize=(8,8))
cax = ax.matshow(u, extent=(0, N*h, M*k, 0), aspect='auto', cmap=cm.coolwarm) 
fig.colorbar(cax)
contour(X, Y, u, 20)
#quiver(X, Y, -u_x, u_y, scale=30)
streamplot(X, Y, -u_x, -u_y);

Aufgabe 5: Wärmeleitungsgleichung¶

Wir betrachten die Wärmeleitungsgleichung \(u_{t}=u_{xx}\) für \(0 \leq x \leq 1\) und \(0 \leq t\) mit den Rand- und Anfangsbedingungen

\(u(0,t) = u(1,t) = 0\)
\(u(x,0) = \sin(\pi x)\)

Lösen Sie das Problem analytisch.
Lösen Sie das Problem numerisch mit der expliziten Methode der finiten Differenzen an den Stützstellen \(x=0, 0.1, 0.2, \ldots, 0.9, 1\) und \(t=0, 0.005, 0.010, 0.015\).
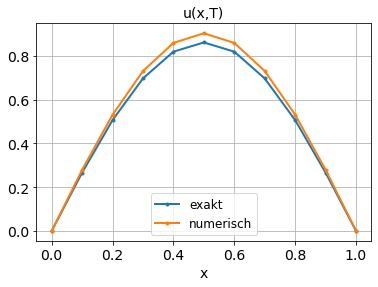
Vergleichen Sie Ihre numerisches Ergebnis mit den analytischen bei \(t=0.015\).

Lösung:

h = 0.1
# x = frange(0, 1, delta=h)
x = arange(0, 1 + h, step=h)

k = 0.005
T = 0.015
# t = frange(0, T, delta=k)
t = arange(0, T, step=k)

a = 1   # alpha der Wärmeleitungsgleichung

M = len(t)  # Anzahl Stützstellen für Zeit
N = len(x)    # Anzahl Stützstellen für Raum

print("Stabilitätsbedingung:", a*k/h**2)
N

Stabilitätsbedingung: 0.4999999999999999

# u(t, x):
u = zeros((M, N))    # Initalisierungmit Nullen
u[0, :] = sin(pi*x)  # Anfangsbedingung für t=0

for m in range(0, M-1):
    for n in range(1,N-1):
        u[m+1,n] = u[m,n] + a*k/h**2*(u[m,n-1] - 2*u[m,n] + u[m,n+1])

u_T = exp(-pi**2*T)*sin(pi*x)

plot(x, u_T    , '.-', label='exakt')
plot(x, u[-1,:], '.-', label='numerisch')
title('u(x,T)')
xlabel("x")
legend()
grid(True)

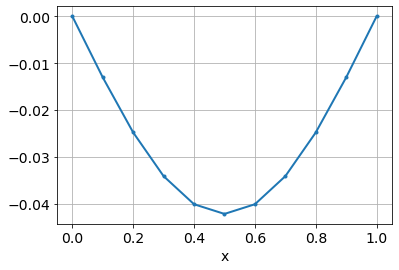
error = u_T - u[-1,:]
plot(x, error, '.-')
xlabel("x")
grid(True)

Technische Mathematik

Numerik

Contents

Numerik¶

Finite Differenzen¶

Crank-Nicolson¶

Galerkin und Finite Elemente¶

Aufgabe 1: Laplacegleichung¶

Aufgabe 2: Wärmeleitungsgleichung¶

Aufgabe 3: Crank-Nicolson, Wärmeleitungsgleichung¶

Aufgabe 4: Laplacegleichung¶

Aufgabe 5: Wärmeleitungsgleichung¶