Übung 2

Lineare Modelle zur Regression und Klassifikation - Monte-Carlo Simulation

Python

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import mglearn

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import GradientBoostingClassifier

# set default values for all plotting:
size=12
plt.rcParams['axes.labelsize']  = size
plt.rcParams['xtick.labelsize'] = size
plt.rcParams['ytick.labelsize'] = size
plt.rcParams['legend.fontsize'] = size
plt.rcParams['figure.figsize'] = 6.29, 6/10*6.29
plt.rcParams['lines.linewidth'] = 1
plt.rcParams['axes.grid'] = True
# print(plt.rcParams)

# import locale                                        #should you want german notation for numbers, then use the locale package
# locale.setlocale(locale.LC_ALL, "deu_deu")
# plt.rcParams['axes.formatter.use_locale'] = True

# Stylefile
# plt.style.use('C:/Users/edel/Documents/Python Scripts/Stylefile/custom_figure_style.mplstyle')

import warnings

warnings.filterwarnings("ignore")

Linear Models for Regression

Übung 1: Lineare Regression von Energiedaten

Fitten Sie ein lineares Regressionsmodell in die Daten der Datei ENERGY.DAT, und stellen Sie Ihr Ergebnis grafisch dar. Verwenden Sie dazu den Scikit-Learn Algorithmus LinearRegression

Lösung:

df = pd.read_csv("daten/ENERGY.DAT", delim_whitespace= True, index_col=0)
df['RGDP'] = df['RGDP']/1000
df['EN']   = df['EN']/1000

X = df['RGDP'].values.reshape(-1,1) # makes it a 2-dim-array
y = df['EN']  # 1-dim array for target vextor is OK too

# we use a split, but could have used the whole data X, y for demonstration too:
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

lr = LinearRegression()
lr.fit(X_train, y_train)

print("Linear Regression:")
print(f"- Training set score: {lr.score(X_train, y_train):.2f}")
print(f"- Test     set score: {lr.score(X_test, y_test):.2f}")

Linear Regression:
- Training set score: 0.96
- Test     set score: 0.89

line = np.linspace(0, 800, 1000)  # 1-dim array
line = np.reshape(line, (-1, 1))  # makes it a 2-dim-array, needed for feature matrix

plt.figure()
plt.scatter(df['RGDP'], df['EN'], color='red',  label='Daten')
plt.plot(line, lr.predict(line),color='black', label='Vorhersagemodell')
plt.xlabel('RGDP')
plt.ylabel('EN')
plt.legend()
plt.grid(True)
plt.tight_layout()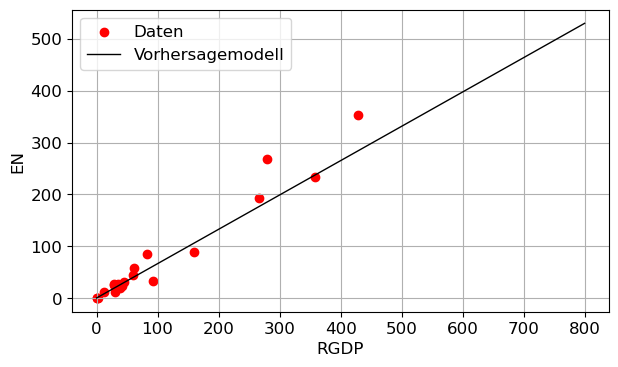

Aufgabe 1: Korrelation und \(R^2\)-Wert

Zeigen Sie an den wave-Daten, die Sie mit X, y = mglearn.datasets.make_wave() laden können, den allgemeinen Zusammenhang, dass im Fall eines einzigen Features die Korrelation \(\text{corr}(y, x_1)\) zwischen Targetvektor \(y\) und Featurevektor \(x_1\) mit dem \(R^2\)-Wert des Fits der linearen Regression \(y \sim x_1\) wie folgt in Beziehung steht:

\[R^2 = \left[\text{corr}(y, x_1)\right]^2\]

Hinweise: Verwenden Sie die Funktion corrcoef.

Lösung:

X, y = mglearn.datasets.make_wave(n_samples=100)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

lr = LinearRegression().fit(X_train, y_train)

R2 = lr.score(X_train, y_train)

Rho = np.corrcoef(y_train, X_train.flatten()) # .flatten() makes it a 1-dim array
rho = Rho[0, 1]

R2 - rho**2

-2.220446049250313e-16

plt.figure()
plt.scatter(X,y,color='red',marker='.')
plt.xlabel('X-Achse')
plt.ylabel('Y-Achse')
plt.grid(True)
plt.tight_layout()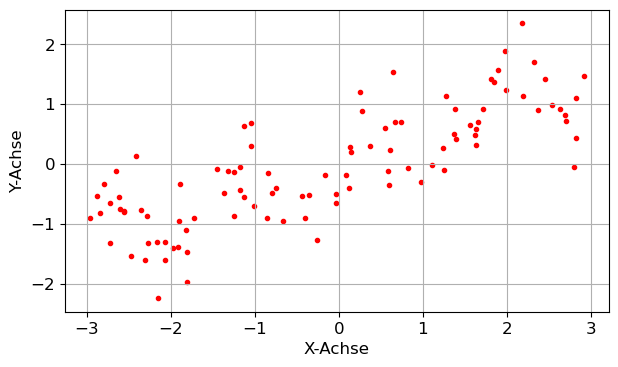

Aufgabe 2: Lineare Regression der Boston House Prices

Verwenden Sie den extended Boston House Prices Datensatz.

1. Erstellen Sie eine lineare Regression mit allen Features und testen Sie das Modell an Testdaten. Ist Ihr lineares Modell evtl. over- oder underfitted?
2. Vergleichen Sie das Ergebnis der linearen Regression mit jener einer kNN-Regression mit 5 Nachbarn.
3. Verwenden Sie eine Lasso-Regression und finden Sie einen optimalen Wert des Regularisierungsparameters.
4. Vergleichen Sie die Regressionskoeffizienten der linearen Regression und der Lasso-Regression über ‘stem’-Plots. Was fällt Ihnen dabei auf?

Lösung:

X, y = mglearn.datasets.load_extended_boston()
X_train, X_test, y_train, y_test = train_test_split(X, y)

print(X.shape)
print(y.shape)

lr = LinearRegression()
lr.fit(X_train, y_train)

print("Linear Regression:")
print(f"- Training set score: {lr.score(X_train, y_train):.2f}")
print(f"- Test     set score: {lr.score(X_test, y_test):.2f}")

(506, 104)
(506,)
Linear Regression:
- Training set score: 0.93
- Test     set score: 0.73

reg = KNeighborsRegressor(n_neighbors=5)
reg.fit(X_train, y_train)

print("kNN-Regression:")
print(f"- Training set score: {reg.score(X_train, y_train):.2f}")
print(f"- Test     set score: {reg.score(X_test, y_test):.2f}")

kNN-Regression:
- Training set score: 0.83
- Test     set score: 0.77

Train_scores=[]
Test_scores=[]
alphas=np.logspace(-5,5,11)

for i in range(len(alphas)):
    lasso = Lasso(alphas[i])
    lasso.fit(X_train,y_train)
    Train_scores.append(lasso.score(X_train,y_train))
    Test_scores.append(lasso.score(X_test,y_test))

plt.figure()
plt.semilogx(alphas,Train_scores,color='red',label='Train-Score Lasso')
plt.semilogx(alphas,Test_scores,color='blue',label='Test-Score Lasso')
plt.axhline(reg.score(X_test,y_test),color='black',ls='dashed',label='KNN')
plt.axhline(lr.score(X_test,y_test),color='black',ls='solid',label='Linear Regression')
plt.ylim(0,1)
plt.xlabel('Alpha (-)')
plt.ylabel('Coefficient of Determination')
plt.legend()
plt.tight_layout()
plt.savefig('Regression_Comparison.jpg',dpi=600)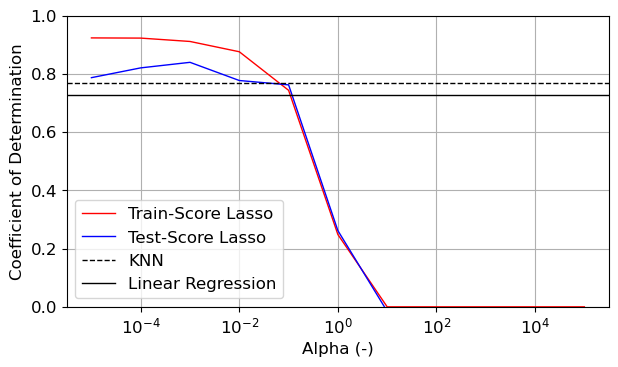

alpha_opt=0.01
lasso_opt=Lasso(alpha=alpha_opt)
lasso_opt.fit(X_train,y_train)

Lasso(alpha=0.01)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

fig=plt.figure(figsize=(6.29,1.2*6.29))
ax=fig.add_subplot(2,1,1)
ax2=fig.add_subplot(2,1,2,sharex=ax)

ax.stem(np.concatenate( ([lr.intercept_], lr.coef_) ),label='Lineare Regression')
# plt.ylim(-20, 20)
ax.legend()
ax.grid(True)

ax2.stem(np.concatenate( ([lasso_opt.intercept_], lasso_opt.coef_) ),label='Lasso Regression, α={:.2f}'.format(alpha_opt))
# plt.ylim(-20, 20)
ax2.set_xlabel('Feature')
ax2.legend()
ax2.grid(True)

Übung 2: Verteilung der Scores, Arithmetisch gemittelter Score

Versuchen Sie die folgende Funktion nachzuvollziehen. Darin werden für einen definierten Algorithmus verschiedene Train_Test_Splits gemacht, um generelle Aussagen über die Qualität einer Vorhersage zu bekommen.

1. Verwenden Sie die folgende Funktion, um sich für 50 unterschiedliche Splits die Testscores sowie den mittleren Score zu berechnen.
2. Stellen Sie die Testscores in Abhängigkeit der Anzahl der Splits dar.
3. Erstellen Sie einen vertikalen KDE (kernel density estimation) - Plot mit dem Seaborn-Paket (sns.kdeplot)

n_splits=10

def Algo_Scores(algo_sel=LinearRegression()):
    Test_Scores=[]
    for i in range(n_splits): 
        X_train, X_test, y_train, y_test = train_test_split(X, y)
        algo=algo_sel
        algo.fit(X_train,y_train)
        Test_Scores.append(algo.score(X_test,y_test))
    Mean_Test_Score=np.mean(Test_Scores)
    return [Test_Scores,Mean_Test_Score]

LR_Test_Scores=Algo_Scores()[0] 
LR_Test_Mean=Algo_Scores()[1] 
print(LR_Test_Mean)

0.8018757007168894

t=np.arange(0,n_splits,1)

plt.figure()
plt.scatter(t,LR_Test_Scores,color='red',label='Test Scores')
plt.axhline(LR_Test_Mean,color='black',ls='solid',label='Mean Test Score')
plt.xlabel('Splits')
plt.ylabel('Testscore')
plt.ylim(0,1)
plt.legend()
plt.tight_layout()

plt.figure()
plt.hist(LR_Test_Scores,bins=25,color='red',density=True,histtype='stepfilled',orientation='horizontal')
plt.xlabel('Number')
plt.ylabel('Testscore')
plt.ylim(0,1)
plt.tight_layout()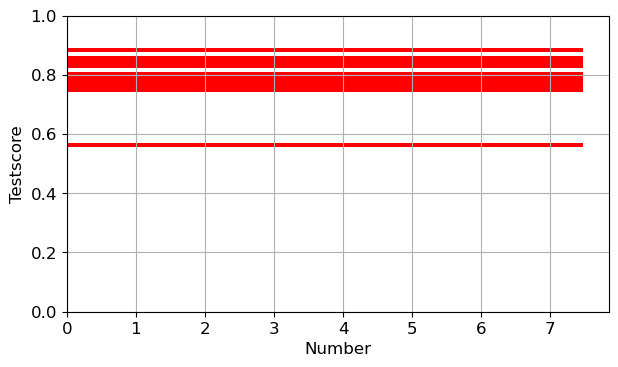

plt.figure()
sns.kdeplot(LR_Test_Scores,color='red',vertical=True,label='Scores',fill=True)
plt.axhline(LR_Test_Mean,color='black',label='Mean Score')
plt.xlabel('Number')
plt.ylabel('Testscore')
plt.ylim(0,1)
plt.legend()
plt.tight_layout()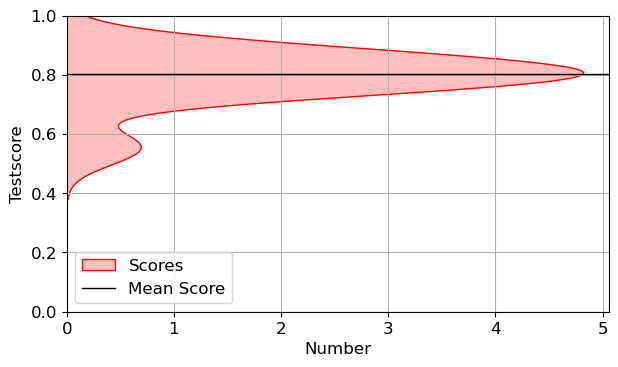

Linear Models for Classification

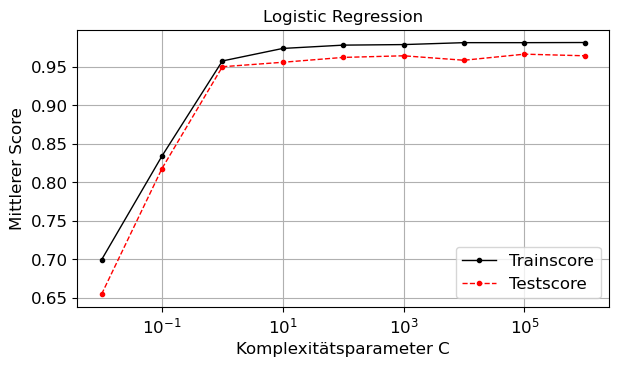
Aufgabe 3: Iris-Datensatz mit LogisticRegression und LinearSVC

Verwenden Sie den Iris Datensatz und untersuchen Sie die Performance des LogisticRegression und des LinearSVC Klassifizierers für unterschiedliche Regularisierungsparameterwerte und mehrere Train-Test-Splits.

Lösung:

iris_dataset = load_iris()

algorithm = 'Logistic Regression'
#algorithm = 'Linear SVC'

C_values = np.logspace(-2, 6, num=9)
number_of_splits = 50

mean_scores_train = []
mean_scores_test  = []

for C in C_values:
    scores_train = []
    scores_test  = []
    for i in range(number_of_splits):
        X_train, X_test, y_train, y_test = train_test_split(iris_dataset['data'], iris_dataset['target'])
        if algorithm == 'Logistic Regression':
            algo = LogisticRegression(C=C, max_iter=1000, penalty="l2", solver='liblinear', 
                                      multi_class='ovr').fit(X_train, y_train)
        elif algorithm == 'Linear SVC':
            algo = LinearSVC(C=C, penalty="l2", dual=False, max_iter=1000).fit(X_train, y_train) 
        scores_train.append(algo.score(X_train, y_train))
        scores_test .append(algo.score(X_test , y_test ))
    mean_scores_train.append(np.mean(scores_train))
    mean_scores_test .append(np.mean(scores_test ))

plt.figure()
plt.title(algorithm)
plt.semilogx(C_values, mean_scores_train, color='black',ls='solid',marker='.', label='Trainscore')
plt.semilogx(C_values, mean_scores_test , color='red',ls='dashed',marker='.',label='Testscore')
plt.xlabel('Komplexitätsparameter C')
plt.ylabel('Mittlerer Score')
plt.legend()
plt.grid(True)
plt.tight_layout()