Lösungen
Contents
Lösungen#
Python-Pakete#
import numpy as np
import matplotlib.pyplot as plt
from scipy import constants
Aufgabe 1: Plotten von Graphen#
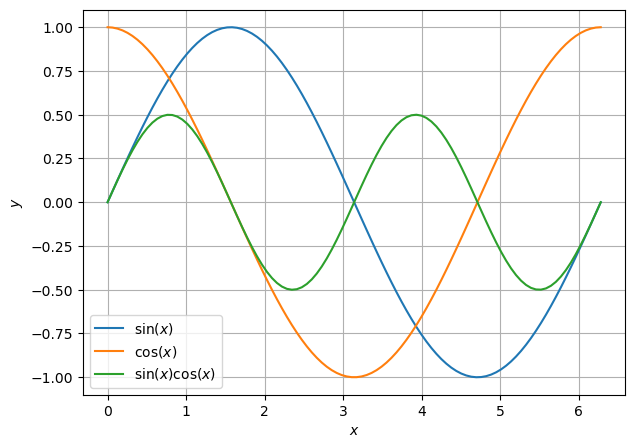
Plotten Sie mit Python im Bereich \([0, 2\pi]\) die Graphen der Funktionen \(\sin(x)\), \(\cos(x)\) und \(\sin(x)\cos(x)\).
Lösung#
x = np.linspace(0, 2*np.pi, 100)
plt.figure(figsize=(7, 5))
plt.plot(x, np.sin(x), label='$\sin(x)$')
plt.plot(x, np.cos(x), label='$\cos(x)$')
plt.plot(x, np.sin(x)*np.cos(x), label='$\sin(x)\cos(x)$')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.grid(True)
plt.legend(loc='best');
Aufgabe 2: Graph plotten, Nullstellen, Polstellen#
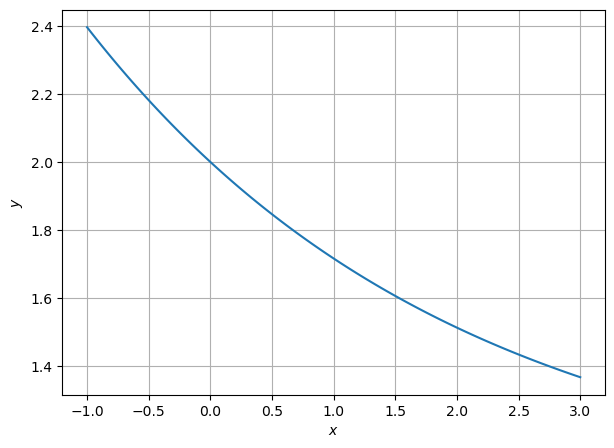
Zeichnen Sie die Funktion \(f(x) = e^{-x/3} + 1\) im Bereich \([-1,3]\).
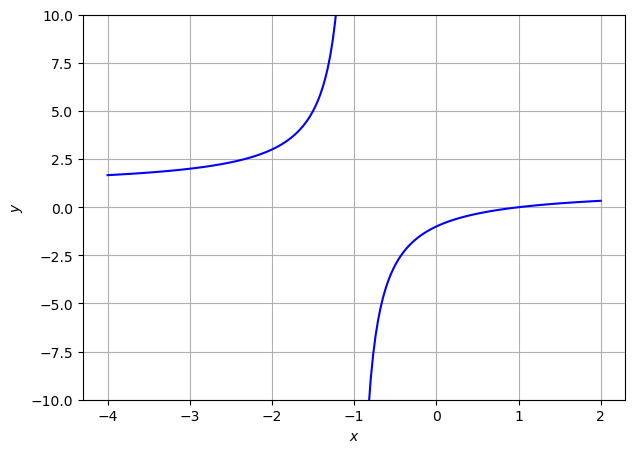
Wo besitzt die Funktion \(f(x)=\frac{x^2 - 2x + 1}{x^2 - 1}\) Nullstellen, wo Polstellen?
Lösung#
Siehe Code.
Siehe Code. Nullstelle bei \(x=1\), Polstelle bei \(x=-1\)
plt.figure(figsize=(7,5))
x = np.linspace(-1, 3, 100)
plt.plot(x, np.exp(-x/3) + 1)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.grid(True)
plt.figure(figsize=(7,5))
x = np.linspace(-4, -1 - 0.02, 100)
plt.plot(x, (x**2 - 2*x + 1)/(x**2 - 1), 'b')
x = np.linspace(-1 + 0.02, 2, 100)
plt.plot(x, (x**2 - 2*x + 1)/(x**2 - 1), 'b')
plt.ylim(-10, 10)
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.grid(True)
Aufgabe 3: Nullstellen#
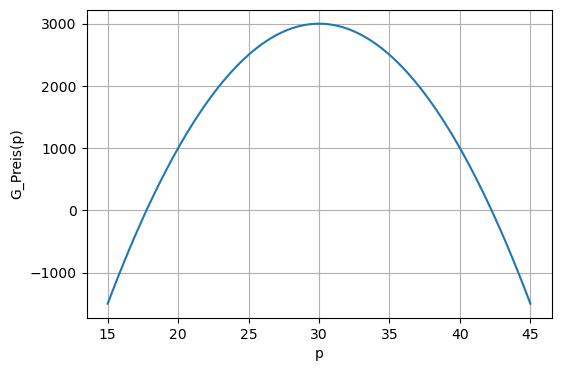
Bestimmen Sie händisch die Nullstellen der Gewinnfunktion \(G_{\text{Preis}}(p) = -20p^2 + 1200p - 15000\) aus der Vorlesung, und überprüfen Sie Ihr Ergebnis mit der Funktion np.roots.
Hinweis: quadratische Gleichungen
Lösung#
Verwende eine Lösungsformel für quadratische Gleichungen, z. B. jene für die Normalform \(x^{2}+px+q=0\):
Für \(-20p^2 + 1200p - 15000 = 0\) folgt \(p_{1,2} = 30 \pm \sqrt{150}\).
p_1 = 30 + np.sqrt(150)
p_2 = 30 - np.sqrt(150)
print(f"{p_1 = }")
print(f"{p_2 = }")
p_1 = 42.24744871391589
p_2 = 17.75255128608411
p = np.linspace(15, 45, num=100)
G_Preis = -20*p**2 + 1200*p - 15000
plt.figure(figsize=(6,4))
plt.plot(p, G_Preis)
plt.xlabel("p")
plt.ylabel("G_Preis(p)")
plt.grid(True)
c = [-20, 1200, -15000]
np.roots(c)
array([42.24744871, 17.75255129])
Aufgabe 4: Definitionsmenge, Wertemenge, Graph#
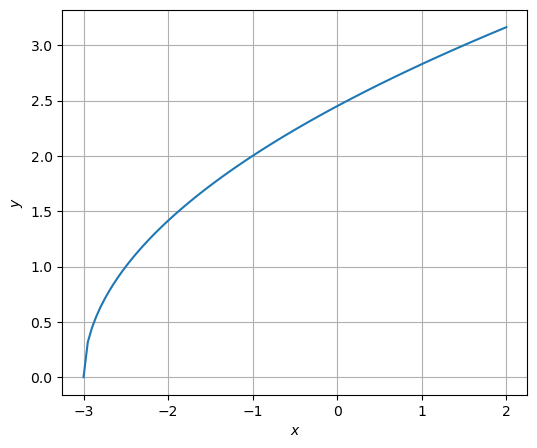
Bestimmen Sie die größtmögliche Definitionsmenge und die zugehörige Wertemenge zur Funktionsgleichung \(y= \sqrt{2x + 6}\). Erstellen Sie eine Wertetabelle, und zeichnen Sie den Graphen.
Lösung#
Die größtmögliche Definitionsmenge ist \([-3,\infty)\). Die zugehörige Wertemenge ist \([0,\infty)\).
def f(x):
return np.sqrt(2*x+6)
x_values = np.arange(-3, 3, step=1)
print("x | f(x)")
print("----------")
for x in x_values:
print(f"{x:2.0f} | {f(x):1.3f}")
x | f(x)
----------
-3 | 0.000
-2 | 1.414
-1 | 2.000
0 | 2.449
1 | 2.828
2 | 3.162
x = np.linspace(-3, 2, 100)
plt.figure(figsize=(6,5))
plt.plot(x, f(x))
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.grid(True)
Aufgabe 5: Zinseszinsrechnung#
Sie veranlagen Ihr Vermögen von \(K_0 =1000\) Euro mit einem fixen jährlichen Zinssatz von \(p=3\,\% = 0.03\).
Bestimmen Sie die Funktionsgleichung der Funktion \(K\), die jedem \(t \in \{0, 1, 2, 3, \ldots\} = \mathbb{N}_0\), den Wert der Veranlagung nach \(t\) Jahren zuordnet. Warum wächst das Vermögen exponentiell?
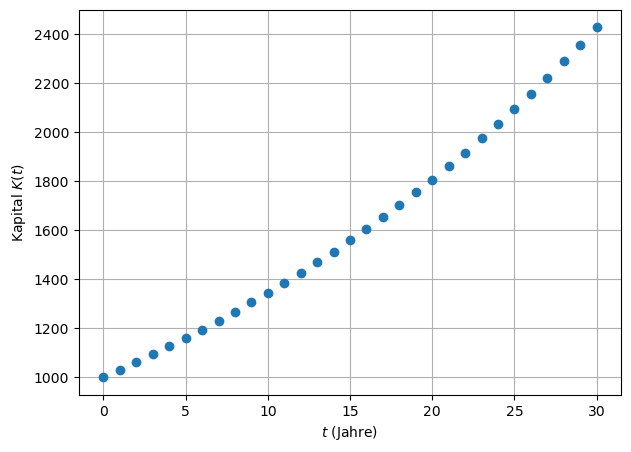
Erstellen Sie einen Plot der Funktion von \(t=0\) bis \(t=30\).
Bestimmen Sie die Funktionsgleichung der Umkehrfunktion von \(K\).
Lösung#
\(K(t) = K_0 (1 + p)^t\) beschreibt exponentielles Wachstum, da das Argument \(t\) im Exponenten ist.
Siehe Code
\(t(K) = \frac{\ln(K/K_0)}{\ln(1 + p)}\)
K0 = 1000
p = 0.03
t = np.arange(0, 31)
K = K0*(1 + p)**t
plt.figure(figsize=(7,5))
plt.plot(t, K, 'o')
plt.xlabel('$t$ (Jahre)')
plt.ylabel('Kapital $K(t)$')
plt.grid(True)
Aufgabe 6: Newtons Abkühlgesetz#
Sie stehen mit Freunden beim Weihnachtsmarkt und haben sich eine heiße Tasse Glühwein gekauft. Die Außentenperatur \(T_A\) beträgt -3 °C, der Glühwein hat anfangs eine Temperatur von \(T(0) = 70\) °C. Das Gespräch kommt auf Newtons Abkühlgesetz
das gemeinsam mit der Anfangsbedingung \(T(0) = 70\) °C die Temperatur \(T(t)\) zu allen späteren Zeiten \(t>0\) h bestimmt. Dabei ist \(\lambda>0\) eine Konstante, die von der Stärke der Wärmedämmung der Tasse abhängt.
Formulieren Sie Newtons Abkühlgesetz in Ihren eigenen Worten.
Welche Einheit hat \(\lambda\) und welche hat \(\frac{1}{\lambda}\)?
Wohin tendiert die Temperatur des Glühweins für große Zeiten? Wie erkennt man das an Newtons Abkühlgesetz?
Zeigen Sie, dass \(T(t) = T_A + (T(0) - T_A)e^{-\lambda t}\) die Anfangsbedingung und Newtons Abkühlgesetz erfüllt.
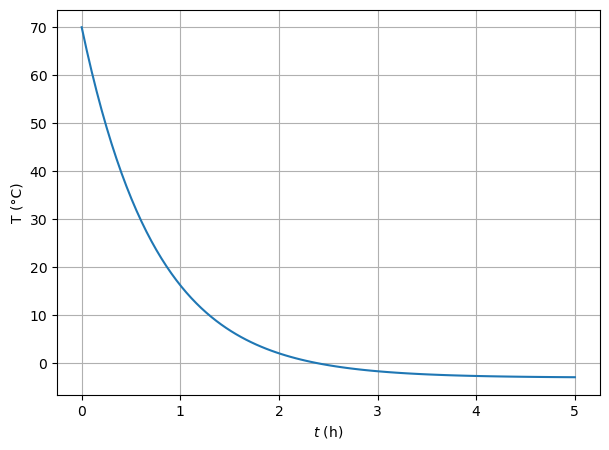
Plotten Sie \(T(t)\) für einen plausiblen \(\lambda\) Wert über \(t\in [0, 2]\).
Lösung#
Die Änderung der Glühweintemperatur ist um so größer, je größer die Temperaturdifferenz zur Außentemperatur und je größer \(\lambda\) ist.
\(\lambda\) hat die Einheit 1/h, \(\frac{1}{\lambda}\) hat die Einheit h.
zur Außentemperatur. Wenn sich die Glühweintemperatur nicht mehr viel ändert, ist \(\dot{T}(t)\simeq 0\), woraus aus Newtons Abkühlgesetz folgt, dass \(T(t) \simeq T_A\).
Einsetzen von \(t=0\) in \(T(t)\). Ableiten liefert \(\dot{T}(t) = -\lambda (T(0) - T_A)e^{-\lambda t}\), was gleich \(-\lambda (T(t) - T_A)\) ist.
Siehe Code.
T_0 = 70 # °C
T_A = -3 # °C
lbd = 1/0.75 # 1/h
t = np.linspace(0, 5, num=100)
T = (T_0 - T_A)*np.exp(-lbd*t) + T_A
plt.figure(figsize=(7,5))
plt.plot(t, T)
plt.xlabel("$t$ (h)")
plt.ylabel("T (°C)")
plt.grid(True)
Aufgabe 7: Radioaktiver Zerfall#
Radiaktiver Zerfall kann durch die Funktion \(N(t) = N_0 e^{-\lambda t}\) beschrieben werden. Dabei bezeichnet \(N(t)\) die Anzahl der zur Zeit \(t\) vorhandenen (d. h. noch nicht zerfallenen) Atome. \(N_0\) ist die Anzahl der zur Zeit \(t = 0\) vorhandenen Atome und \(\lambda > 0\) ist die dem Material eigene Zerfallskonstante, die angibt, wie schnell oder wie langsam der Stoff zerfällt.
Radium Ra\(^{226}_{88}\) hat eine Halbwertszeit von 1580 Jahren. Nach welcher Zeit liegen von diesem radioaktiven Stoff nur noch 1 % der anfänglich vorhandenen Atome vor?
Lösung#
Quelle: Stry, Schwenkert: Mathematik kompakt. Seite 94
Die Halbwertszeit hängt mit der Zerfallskonstante über \(T_{1/2} = \frac{\ln(2)}{\lambda}\) zusammen, siehe Stry, Schwenkert: Mathematik kompakt. Seite 94. Wir bezeichnen mit \(T_{0.01}\) jene Zeit, nach welcher vom radioaktiven Stoff nur noch 1 % vorliegen. Dann gilt:
Aufgabe 8: injektiv, surjektiv, bijektiv, Umkehrfunktion#
Bestimmen Sie von folgenden Funktionen, ob sie injektiv, surjektiv oder bijektiv sind oder keine dieser Eigenschaften haben:
\(f:(-\frac{\pi}{2}, \frac{\pi}{2}) \to \mathbb{R}: f(x) = \sin(x)\)
\(f:(-\frac{\pi}{2}, \frac{\pi}{2}) \to (-1, 1) : f(x) = \sin(x)\)
\(f:\mathbb{R} \to [0,\infty): f(x) = x^2\)
\(f:\mathbb{R} \to \mathbb{R}: f(x) = x^3\)
\(f:\mathbb{R} \to \mathbb{R}: f(x) = x^2\)
Bestimmen Sie die Umkehrfunktion von \(f(x) = 5e^{-\frac{x}{7}} - 2\) mit maximalem Definitionsbereich. Geben Sie diesen Definitionsbereich, einen passenden Wertebereich und die Funktionsgleichung an.
Lösung#
Lösung:
injektiv
bijektiv
surjektiv
bijektiv
keine dieser Eigenschaften
\(D = (-2, \infty)\), \(W = \mathbb{R}\), \(f^{-1}: W \to D: f^{-1}(y) = -7\ln\left(\frac{y + 2}{5}\right)\)
Aufgabe 9: Trigonometrische Funktionen, Strahlensatz#
Führen Sie die Argumentationen im Abschnitt “Trigonometrische Funktionen” der Vorlesung mit Hilfe des Strahlensatzes im Detail aus.
Lösung#
Aufgabe 10: Symmetrie von Funktionen - gerade, ungerade#
Welche der folgenden Funktionen ist gerade, ungerade oder weder noch?
\(f(x)= 4x^2 - 16\)
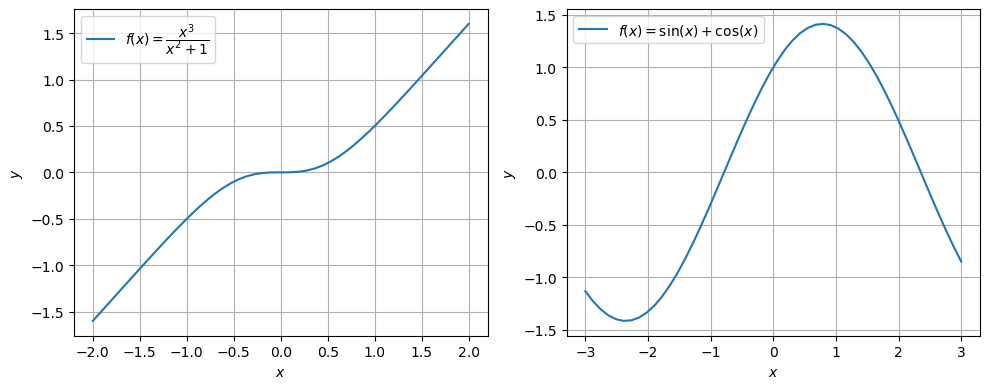
\(f(x)= \dfrac{x^3}{x^2 + 1}\)
\(f(x)= \sin(x)\cos(x)\)
\(f(x)= \sin(x) + \cos(x)\)
\(f(x)= \dfrac{1}{x - 1}\)
Lösung#
gerade
ungerade
ungerade
weder gerade noch ungerade
weder gerade noch ungerade
plt.figure(figsize=(10,4))
plt.subplot(1,2,1)
x = np.linspace(-2, 2)
y = x**3/(x**2 + 1)
plt.plot(x, y, label="$f(x)= \dfrac{x^3}{x^2 + 1}$")
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend()
plt.grid(True)
plt.subplot(1,2,2)
x = np.linspace(-3, 3)
y = np.sin(x) + np.cos(x)
plt.plot(x, y, label="$f(x)= \sin(x) + \cos(x)$")
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend()
plt.grid(True)
plt.tight_layout()
Aufgabe 11: (un)gerade Funktionen#
Welche der folgenden Funktionen sind gerade, ungerade oder weder noch?
\(f(x)=4\sin(2x)\)
\(f(x)=\frac{x^2-1}{1+x^2}\)
\(f(x)=e^{-x}\)
Lösung#
ungerade
gerade
weder gerade noch ungerade
Aufgabe 12: (un-)gerader Anteil#
Jede Funktion \(f(x)\) lässt sich in einen geraden Anteil \(f_g(x)\) und einen ungeraden Anteil \(f_u(x)\) aufspalten:
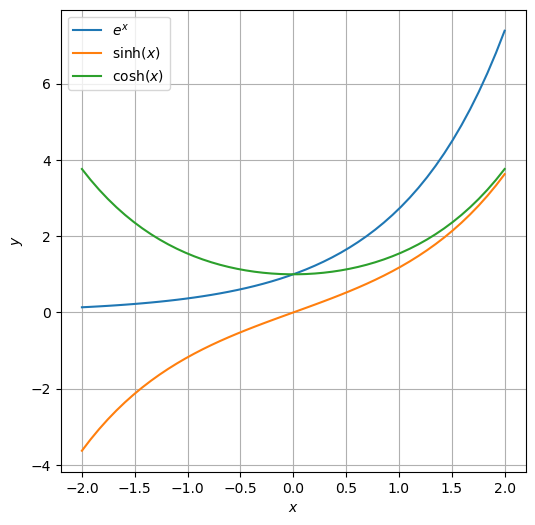
Bestimmen Sie den geraden und den ungeraden Anteil von \(e^{x}\). Plotten Sie alle drei Funktionen. Vergleichen Sie Ihr Ergebnis mit den Definitionen der Funktionen \(\cosh(x)\) und \(\sinh(x)\).
Lösung#
\(f_g(x) = \frac{1}{2}(e^x + e^{-x}) = \cosh(x)\)
\(f_u(x) = \frac{1}{2}(e^x - e^{-x}) = \sinh(x)\)
Links:
x = np.linspace(-2, 2)
plt.figure(figsize=(6,6))
plt.plot(x, np.exp(x) , label='$e^x$')
plt.plot(x, np.sinh(x), label='$\sinh(x)$')
plt.plot(x, np.cosh(x), label='$\cosh(x)$')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.legend()
plt.grid(True)
Aufgabe 13: Monotonieeigenschaften, Periode, gerade, ungerade#
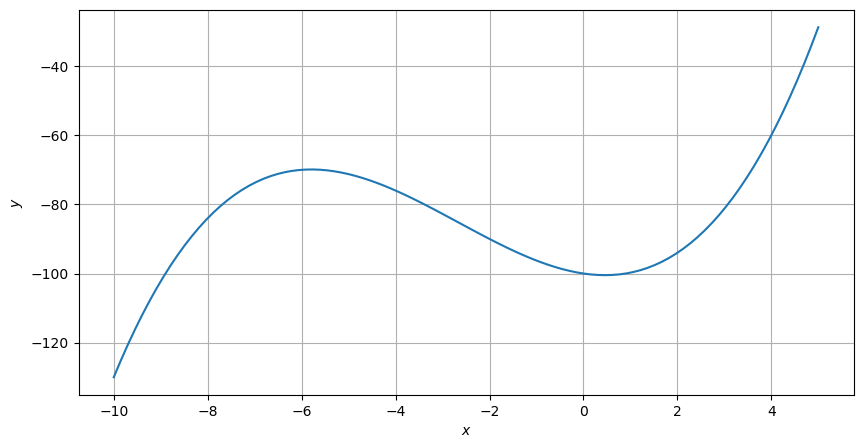
Bestimmen Sie mit Hilfe eines Plots, in welchen Intervallen das Polynom \(f(x) = 0.25x^3 + 2x^2 - 2x - 100\) welche Monotonieeigenschaften hat.
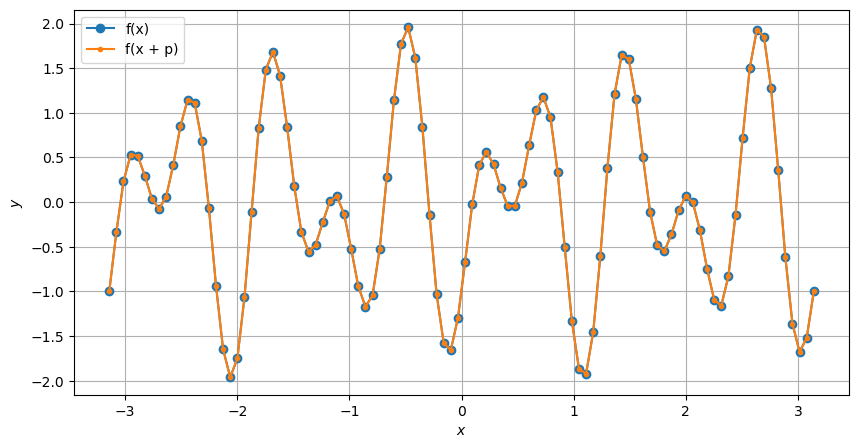
Welche kleinste Periode besitzt die Funktion \(f(x) = \sin(10x) - \cos(6x)\)?
Bestimmen Sie von folgenden Funktionen, ob sie gerade, ungerade oder keine dieser Eigenschaften haben:
\(f(x) = -3x^2 + x^6\)
\(f(x) = \frac{x^2}{\cos(x) + 1}\)
\(f(x) = \tan(x)\)
\(f(x) = e^x\)
Lösung#
Siehe Code unten.
streng monoton steigend von \(-\infty\) bis ca. -6
streng monoton fallend von ca. -6 bis ca. 0.5
streng monoton steigend von ca. 0.5 bis \(\infty\)
Die Perioden \(p\) von \(\sin(10x)\) erfüllen \(\sin(10(x + p)) = \sin(10x)\). Daher muss gelten \(10x + 10p = 10x + n2\pi\) für \(n \in \{1, 2, 3, \ldots\} = \mathbb{N}\). Also \(p = n \frac{2\pi}{10}\). Analog erfüllen die Perioden \(\bar{p}\) von \(\cos(6x)\) die Bedingung \(\bar{p} = \bar{n} \frac{2\pi}{6}\) für \(\bar{n} \in \mathbb{N}\). Wir suchen die kleinste gemeinsame Periode \(p = \bar{p}\), woraus folgt dass \(\frac{n}{10}=\frac{\bar{n}}{6}\) oder \(n = \frac{5}{3}\bar{n}\). Die kleinste Lösung ist \(\bar{n}=3\) und \(n=5\), also die Periode \(p = \bar{p} = \pi\).
1. gerade
2. gerade
3. ungerade
4. keine dieser Eigenschaften
# x = np.linspace(-15, 10, num=100)
x = np.linspace(-10, 5, num=100)
y = 0.25*x**3 + 2*x**2 - 2*x - 100
plt.figure(figsize=(10,5))
plt.plot(x, y)
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.grid(True)
x = np.linspace(-np.pi, np.pi, num=100)
def f(x):
return np.sin(10*x) - np.cos(6*x)
p = np.pi
plt.figure(figsize=(10,5))
plt.plot(x, f(x) , 'o-', label='f(x)')
plt.plot(x, f(x + p), '.-' , label='f(x + p)')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.legend()
plt.grid(True)
Aufgabe 14: Verschieben und Skalieren von Graphen#
Wie ändert sich die Funktionsgleichung \(y = x^2 - \sin(x) + 3\), wenn deren Graph um drei Einheiten in die positive \(x\)-Richtung und um zwei Einheiten in die negative \(y\)-Richtung verschoben wird?
Macht es einen Unterschied, ob man \(y = x^2\) zuerst um den Faktor zwei in \(x\)-Richtung skaliert und danach drei Einheiten in die positive \(x\)-Richtung verschiebt, oder zuerst drei Einheiten in die positive \(x\)-Richtung verschiebt und danach um den Faktor zwei in \(x\)-Richtung skaliert?
Lösung#
\(y = (x-3)^2 - \sin(x-3) + 1\)
Ja.
Aufgabe 15: Verschieben eines Graphen#
Die Funktion \(f(x) = 2x^2 - 16x + 28.5\) entsteht durch Verschieben der Funktion \(g(x) = 2x^2\) um \(a\) Einheiten in die \(x\)-Richtung und \(b\) Einheiten in die \(y\)-Richtung.
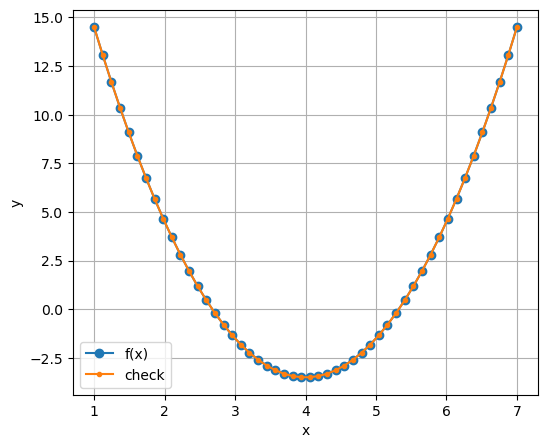
Zeichnen Sie den Graph von \(f\) im \(x\)-Intervall \([1,7]\).
Berechnen Sie \(a\) und \(b\).
Lösung#
Siehe Code
\(a=4\) und \(b=-3.5\)
x = np.linspace(1,7)
y = 2*x**2 - 16*x + 28.5
a = 4
b = -3.5
y_check = 2*(x - a)**2 + b
plt.figure(figsize=(6,5))
plt.plot(x, y , 'o-', label="f(x)")
plt.plot(x, y_check, '.-', label="check")
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
Aufgabe 16: geometrische Operationen am Graphen#
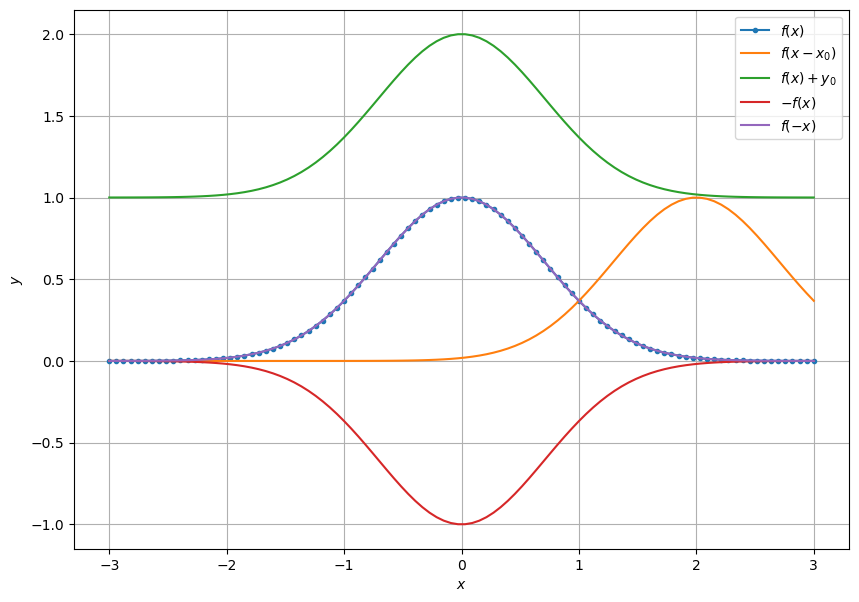
Überprüfen Sie alle geometrische Operationen der Vorlesung am Graphen der Funktion \(f(x) = e^{-x^2}\).
Welche geometrischen Operationen ändern die Symmetrie einer Funktion (gerade oder ungerade) nicht? Begründen Sie Ihre Antwort.
Lösung#
x = np.linspace(-3, 3, num=100)
f = lambda x: np.exp(-x**2)
x_0 = 2
y_0 = 1
plt.figure(figsize=(10,7))
plt.plot(x, f(x) , '.-', label='$f(x)$')
plt.plot(x, f(x - x_0), label='$f(x - x_0)$')
plt.plot(x, f(x) + y_0, label='$f(x) + y_0$')
plt.plot(x, -f(x) , label='$-f(x)$')
plt.plot(x, f(-x) , label='$f(-x)$')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.legend()
plt.grid(True)
plt.figure(figsize=(7,7))
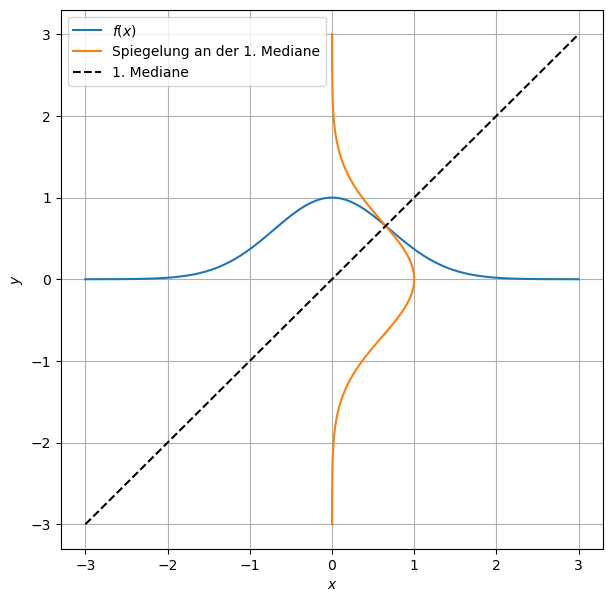
plt.plot(x, f(x), label='$f(x)$')
plt.plot(f(x), x, label='Spiegelung an der 1. Mediane')
plt.plot(x, x, '--k', label='1. Mediane')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.legend()
plt.grid(True)
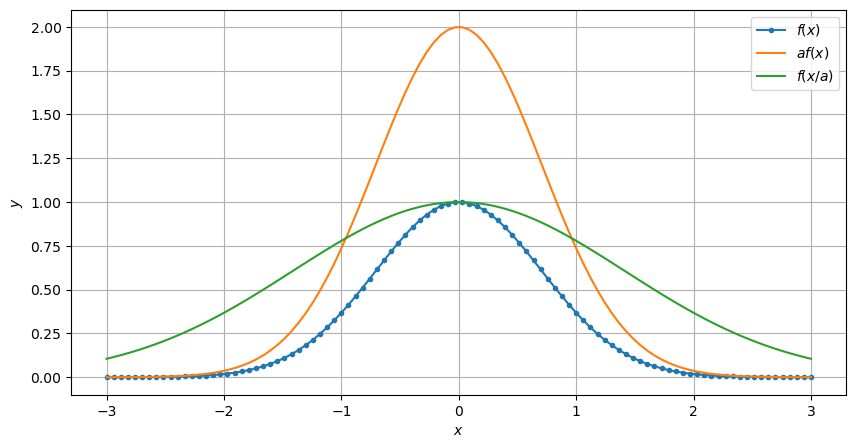
a = 2
plt.figure(figsize=(10,5))
plt.plot(x, f(x) , '.-', label='$f(x)$')
plt.plot(x, a*f(x) , '-' , label='$af(x)$')
plt.plot(x, f(x/a) , '-' , label='$f(x/a)$')
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.legend()
plt.grid(True)
Aufgabe 17: Fallschirmspringen#
Beim Fallschirmspringen gilt unter der Annahme, dass der Luftwiderstand \(R\) der Fallgeschwindigkeit \(v\) proportional ist (d. h. \(R = cv\) für eine Konstante \(c\)), das folgende Geschwindigkeit-Zeit-Gesetz:
Dabei bedeuten
\(m\): Masse des Fallschirmspringers inkl. Fallschirm
\(g\): Erdbeschleunigung
\(c >0\): Reibungsfaktor
Aufgaben:
Welche Endgeschwindigkeit \(v_{E}\) erreicht der Fallschirmspringer? Gehen Sie dafür von einer theoretisch unendlich langen Fallzeit aus.
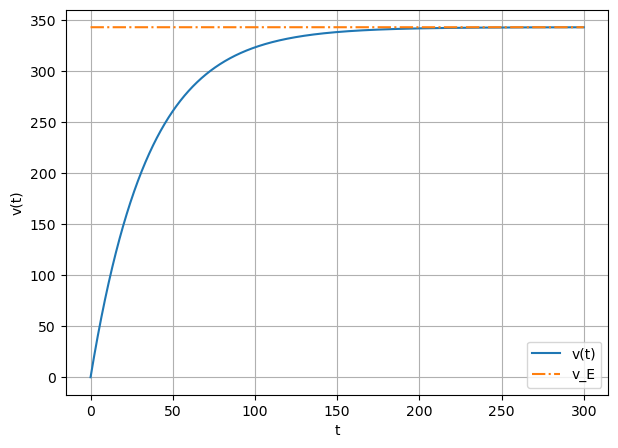
Plotten Sie das Geschwindgkeit-Zeit-Gesetz im Bereich 0 s bis 300 s. Verwenden Sie \(g = 9.81\) m/s\(^2\) , \(m = 70\) kg und \(c = 2\) Ns/m.
Nach welcher Zeit \(\tau\) wird die halbe Endgeschwindigkeit erreicht? Kontrollieren Sie Ihr Ergebnis, indem Sie die ermittelte Zeit \(\tau\) in das Geschwindigkeit-Zeit-Gesetz einsetzen und mit der in 2. ermittelten, halbierten Geschwindigkeit vergleichen.
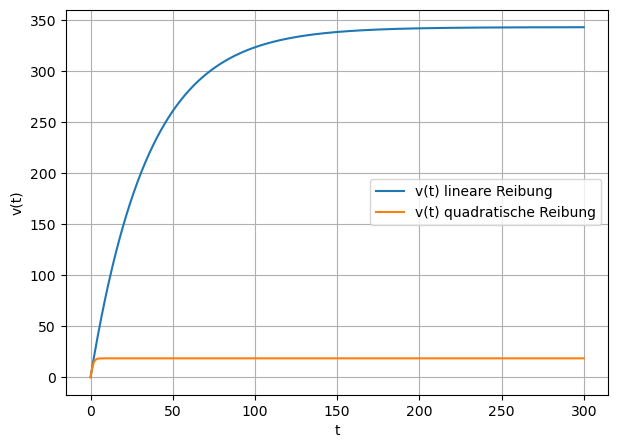
Wird beim freien Fall der Lufwiderstand durch eine dem Quadrat der Fallgeschwindigkeit proportionale Reibungskraft \(R = cv^2\) berücksichtigt, so erhält man das folgende Geschwindigkeit-Zeit-Gesetz
\[v(t) = \sqrt{\frac{mg}{c}}\tanh\left(\sqrt{\frac{gc}{m}}t\right)\]Plotten Sie die beiden Geschwindigkeit-Zeit-Gesetze in einer Grafik.
Lösung#
\(v_{E}=\lim\limits_{t \to \infty} \frac{mg}{c}(1-e^{-\frac{c}{m}t}) = \frac{mg}{c}\)
Siehe Code.
Siehe folgende Rechnung:
\begin{align} \frac{v_{E}}{2} &= v(\tau)\ \frac{v_{E}}{2} &= \frac{mg}{c}(1-e^{-\frac{c}{m}\tau})\ \frac{v_{E}}{2} &= v_E(1-e^{-\frac{c}{m}\tau})\ e^{-\frac{c}{m}\tau}&=\frac{1}{2}\ -\frac{c}{m}\tau \ln(e)&= \ln(1)-\ln(2)\ -\frac{c}{m}\tau &= -\ln(2)\ \tau &= \frac{m}{c}\ln(2) \end{align}
Siehe Code.
g = constants.g #(m/s^2)
m = 70.0 #(kg)
c = 2.0
t = np.arange(0, 300, 0.1)
v = m*g/c*(1 - np.exp(-c/m*t))
v_E = m*g/c*np.ones_like(t)
plt.figure(figsize=(7,5))
plt.plot(t, v ,label="v(t)")
plt.plot(t, v_E, "-.", label="v_E")
plt.xlabel("t")
plt.ylabel("v(t)")
plt.legend()
plt.grid()
tau = m/c*np.log(2)
v_E2B = (m*g)/c*(1-np.exp(-c/m*tau))
v_E2K = (m*g)/(2*c) # Kontrollwert
print(f"Berechneter Wert: {v_E2B}")
print(f"Kontrollwert: {v_E2K}")
Berechneter Wert: 171.61637499999995
Kontrollwert: 171.61637499999998
g = constants.g #(m/s^2)
m = 70.0 #(kg)
c = 2.0
t = np.arange(0, 300, 0.1)
v_1 = m*g/c*(1 - np.exp(-c/m*t))
v_2 = np.sqrt(m*g/c)*np.tanh(np.sqrt(g*c/m)*t)
plt.figure(figsize=(7,5))
plt.plot(t, v_1, label="v(t) lineare Reibung")
plt.plot(t, v_2, label="v(t) quadratische Reibung")
plt.xlabel("t")
plt.ylabel("v(t)")
plt.legend()
plt.grid()
Aufgabe 18: Lösungsformel der quadratischen Gleichung#
Eine allgemeine quadratische Gleichung
mit \(a\neq 0\) kann in der folgenden Form geschrieben werden
mit \(p:=\frac{b}{a}\) und \(q:=\frac{c}{a}\).
Formen Sie die Gleichung \(x^2+px+q=0\) mittes Quadratischer Ergänzung um, und zeigen Sie, dass die Lösungen durch
gegeben sind.
Lösung#
\begin{align} x^2+px+q &= 0\ x^2+px+\left(\frac{p}{2}\right)^2-\left(\frac{p}{2}\right)^2+q &= 0\ \left(x+\frac{p}{2}\right)^2 &= \left(\frac{p}{2}\right)^2-q\ x+\frac{p}{2} &= \pm\sqrt{\left(\frac{p}{2}\right)^2-q}\ x &= -\frac{p}{2}\pm\sqrt{\left(\frac{p}{2}\right)^2-q} \end{align}
Aufgabe 19: Goldener Schnitt#
In der Geomtrie, Architektur, Kunst und in vielen anderen Gebieten wird die Zahl \(\Phi = \frac{1+\sqrt{5}}{2}\) als Maß für Schönheit verwendet. Diese Zahl \(\Phi\) wird als Goldener Schnitt oder auch als Goldene Zahl bezeichnet.

(Quelle: Abbildungen)
Der goldene Schnitt wir als Teilungsverhältnis einer Streck definiert, bei dem das Verhältnis des Ganzen zu seinem größeren Teil gleich dem Verhältnis des größeren zum kleineren ist .
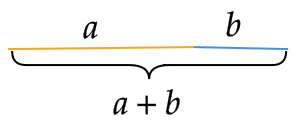
Formen Sie diese Gleichung zu einer quadratischen Gleichung um, die nur noch \(\Phi\) als Variable enthällt, und lösen Sie die resultierende quadratische Gleichung. Zeigen Sie, dass \(\Phi = \frac{1+\sqrt{5}}{2}\) eine Lösung der Gleichung ist.
Lösung#
\begin{align} \frac{a}{b} &= \frac{a+b}{a}\ \frac{a}{b} &= 1+\frac{b}{a}\ \Phi &= 1+\frac{1}{\Phi}\ \Phi^2-\Phi-1 &= 0\ \Phi_{1,2} &= \frac{1\pm\sqrt{5}}{2} \end{align}
Aufgabe 20: Fibonacci Folge#
Aus der Fibonacci Folge lässt sich die Goldene Zahl folgern. Die Fibonacci Folge ist wie folgt definiert
mit \(f_{0} = 0\) und \(f_{1} = 1\). Die ersten Folgenglieder sind \(0,1,1,2,3,5,8,13,...\).
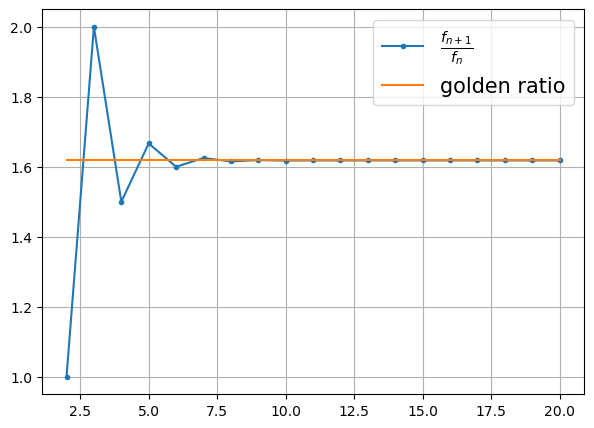
Plotten Sie das Verhältnis \(\frac{f_{n+1}}{f_{n}}\) bis zu \(n=20\) und die Goldene Zahl in einer Abbildung. Was beobachten Sie?
Lösung#
def fib(n): # rekursive Funktion
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
fib_list = []
for i in range(21):
fib_list.append(fib(i))
Ratio_list = []
for i in range(2, len(fib_list)):
Ratio_list.append(fib_list[i]/fib_list[i-1])
golden_Ratio = [(1 + np.sqrt(5))/2 for i in range(2,len(fib_list))]
plt.figure(figsize=(7,5))
plt.plot(list(range(2,len(fib_list))), Ratio_list, ".-", label=r"$\frac{f_{n+1}}{f_{n}}$")
plt.plot(list(range(2,len(fib_list))), golden_Ratio, label="golden ratio")
plt.legend(fontsize=15)
plt.grid()
Aufgabe 21: Fehlersuche 1#
Finden Sie den Fehler in der folgenden Berechnung. Welche mathematische Regel wird hier verletzt?
Lösung#
Aus \(a=b\) folgt \(a^2-ab=0\). In der vorletzten Gleichung wird durch Null dividiert. Dieses Beispiel soll aufzeigen, dass auf Divisionen durch Null geachter werden muss.
Aufgabe 22: Fehlersuche 2#
Finden sie den Fehler in der folgenden Rechnung. Wie kann sie korrigiert werden?
Lösung#
Aus \(a^2 = b^2\) kann nicht alleinig \(a=b\) gefolgert werden, sondern \(a=b\) oder \(a=-b\). Die Rechnung stimmt, wenn für die dritte Gleichung folgendes verwendet wird:
Dieses Beispiel soll die Wichtigkeit des Zusammenhangs \(\sqrt{x^2}=|x|\) hervorheben.
Aufgabe 23: Kondensatorspannung#
Beim Aufladen eines Kondensators steigt die Kondensatorspannung \(u\) (in Volt) im Laufe der Zeit \(t\) (in Sekunden) nach dem Exponentialgesetz
Bestimmen Sie per Handrechnung die Zeitkonstate \(\tau\) aus dem Messwert \(u(2) = 80\).
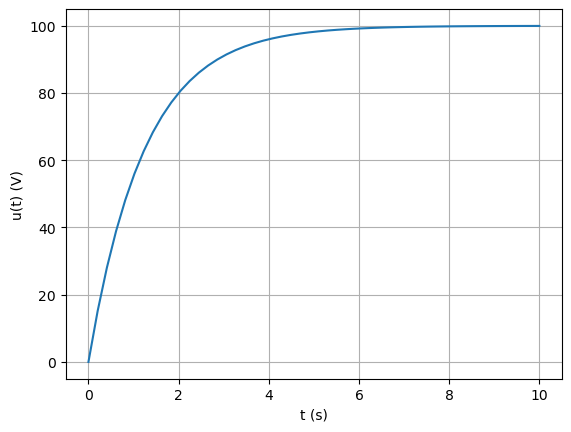
Plotten Sie mit Python den Spannungsverlauf im Kondensator.
Welchen Endwert \(u_E\) erreicht die am Kondensator liegende Spannung? Nach welcher Zeit wird der halbe Endwert erreicht?
Berechnen Sie die Kondensatorspannung zum Zeitpunkt \(t = 5s\)
Lösung#
# 1)
tau = -2/np.log(0.2) # Einheit (s)
print(f"{tau = :.3f} s")
tau = 1.243 s
# 2)
t = np.linspace(0, 10, 50)
def u(t):
return 100*(1 - np.exp(-t/tau))
plt.plot(t, u(t))
plt.xlabel("t (s)")
plt.ylabel("u(t) (V)")
plt.grid(True)
# 3)
# lim t -> inf u(t) = 100 V
print(f"Endwert = 100 V")
# t_halb = tau*ln(2)
print(f"Zeit des halben Endwerts {tau*np.log(2) = :.3f} s")
# 4)
print(f"Kondensatorspannung zum Zeitpunkt t = 5: {u(5):.3}V")
Endwert = 100 V
Zeit des halben Endwerts tau*np.log(2) = 0.861 s
Kondensatorspannung zum Zeitpunkt t = 5: 98.2V
Aufgabe 24: Luftdruck#
Zwischen dem Luftdruck \(p\) (in bar) und der Höhe \(h\) (gemessen in Metern über dem Meeresniveau) gilt unter der Annahme konstanter Lufttemperatur der folgende Zusammenhang:
Parameterwerte: Luftdruck an der Erdoberfläche \(p_0 = 1.013\) bar, \(\alpha = 7991\) m
Wie groß ist der Luftdruck in 10 km Höhe?
Wie muss die Bildmenge gewählt werden, damit die Funktion \(p(h)\) surjektiv ist? Ist die Funktion auch injektiv und somit bijektiv?
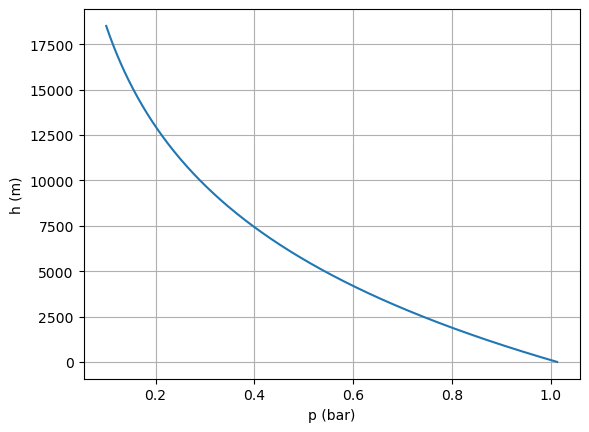
Geben Sie, falls die Funktion invertierbar ist, die Höhe \(h\) als Funktion \(h(p)\) des Luftdruckes \(p\) an, und plotten Sie ihren Graphen mit Python.
In welcher Höhe hat sich der Luftdruck halbiert?
Lösung#
# Parameterwerte:
p0 = 1.013 # bar
alpha = 7991 # m
# 1)
def p(h):
return p0*np.exp(-h/alpha)
print(f"Luftdruck auf Höhe 10 km: {p(10*10**3):.3} bar")
Luftdruck auf Höhe 10 km: 0.29 bar
# 2)
# Y = [1.013, 0)
# 3)
def h(p):
return -alpha*np.log(p/p0)
p_values = np.linspace(0 + 0.1, 1.013, 500)
plt.plot(p_values, h(p_values))
plt.xlabel("p (bar)")
plt.ylabel("h (m)")
plt.grid(True)
# 3)
print(f"Höhe mit halbem Luftdruck (p0/2): {h(p0/2):.5} m")
print(f"Höhe mit halbem Luftdruck (p0/2): {alpha*np.log(2):.5} m")
Höhe mit halbem Luftdruck (p0/2): 5538.9 m
Höhe mit halbem Luftdruck (p0/2): 5538.9 m

