Vorlesung
Contents
Vorlesung#
Konfiguration und Python-Pakete#
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D
Lineare Approximation#
Wir betrachten die Abhängigkeit einer Größe \(y\) von \(n\) anderen Größen \(x_1, x_2, \ldots , x_n\), also eine Funktion \(y = f(x_1, x_2, \ldots , x_n),\) oder kurz \(y(x_1, x_2, \ldots , x_n)\). In der mehrdimensionalen Differentialrechnung wird die Änderung von \(y\) pro Änderung von einem \(x_k\) untersucht.
Wir behandeln zuerst den zweidimensionalen Fall, den wir als \(z = f(x, y)\) schreiben.
Graphische Darstellungen#
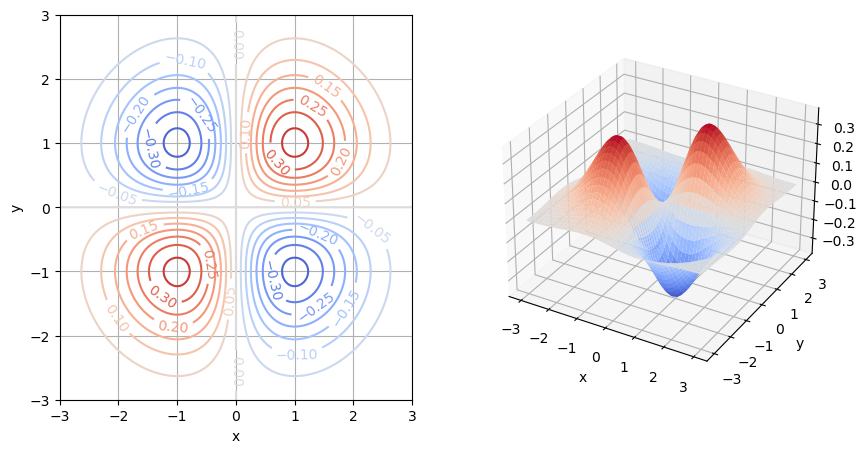
als 3-dim. Graph
mit Höhenschichtlinien auch Konturlinien genannt: \(z\) ist die Höhe, die von den “Landkarten”-Koordinaten \(x\) und \(y\) abhängt.
x = np.linspace(-3, 3, 200)
y = np.linspace(-3, 3, 200)
X, Y = np.meshgrid(x, y)
Z = X*Y*np.exp(-0.5*(X**2 + Y**2))
fig = plt.figure(figsize=(10,5))
ax = fig.add_subplot(1, 2, 2, projection='3d')
ax.plot_surface(X, Y, Z, cmap='coolwarm')
ax.view_init(azim = -60, elev = 30)
plt.xlabel('x')
plt.ylabel('y')
plt.subplot(1, 2, 1)
cs = plt.contour(X, Y, Z, 15, cmap='coolwarm')
plt.clabel(cs, inline=1)
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
Nomenklatur#
Für \(z = f(x, y)\) verwenden wir folgende Bezeichnungen:
\((x_0, y_0)\) ist die Stelle (Argument, Input), an der die Änderung der Funktion linear approximiert wird.
\(\Delta x\) ist die Differenz (Änderung) der Inputgröße \(x\) bei \((x_0, y_0)\), \(\Delta y\) ist die Differenz (Änderung) der Inputgröße \(y\) bei \((x_0, y_0)\).
\(\text{d}x\) ist die lineare Approximation von \(\Delta x\), \(\text{d}y\) ist die lineare Approximation von \(\Delta y\). Es gilt analog zum eindimensionalen Fall \(\text{d}x = \Delta x\) und \(\text{d}y = \Delta y\). Wir schreiben vorwiegend \(\text{d}x\) und \(\text{d}y\).
\(\Delta z\) ist die wahre Differenz (Änderung) der Outputgröße \(z\) bei Änderung der Inputgröße um \(\Delta x\) und \(\Delta y\) bei \((x_0, y_0)\).
\(\text{d}z\) ist die lineare Approximation von \(\Delta z\).
Partielle Ableitungen#
hängt im allgemeinen nicht-linear von \(\Delta x\) und \(\Delta y\) ab. Die lineare Approximation \(\text{d}z\) dieser Abhängigkeit ist für zweidimensionale Funktionen von der Form \(\text{d}z = k_x\,\text{d}x + k_y\,\text{d}y\) für bestimmte Zahlen \(k_x\) und \(k_y\). Diese Zahlen sind die Steigungen der Tangenten an den Funktionsgraphen in die \(x\)- bzw. \(y\)-Richtung bei \((x_0, y_0)\) und heißen die partiellen Ableitung \(\frac{\partial f}{\partial x}(x_0, y_0)\) und \(\frac{\partial f}{\partial y}(x_0, y_0)\) der Funktion \(f\) bei \((x_0, y_0)\) nach \(x\) und nach \(y\):
Ausführlich:
Die partielle Ableitung von \(f\) bei \((x_0, y_0)\) in Richtung \(x\) wird als \(\frac{\partial f}{\partial x}(x_0, y_0)\) geschrieben. Sie gibt die Änderungsrate von \(f\) bei \((x_0, y_0)\) pro \(x\)-Einheit an und entspricht der Steigung der Tangente in \(x\)-Richtung an den Graphen von \(f\) bei \((x_0, y_0)\). Die partielle Ableitung von \(f\) bei \((x_0, y_0)\) in Richtung \(x\) wird durch Konstanthalten von \(y\) und Ableiten nach \(x\) berechnet.
Die partielle Ableitung von \(f\) bei \((x_0, y_0)\) in Richtung \(y\) wird als \(\frac{\partial f}{\partial y}(x_0, y_0)\) geschrieben. Sie gibt die Änderungsrate von \(f\) bei \((x_0, y_0)\) pro \(y\)-Einheit an und entspricht der Steigung der Tangente in \(y\)-Richtung an den Graphen von \(f\) bei \((x_0, y_0)\). Die partielle Ableitung von \(f\) bei \((x_0, y_0)\) in Richtung \(y\) wird durch Konstanthalten von \(x\) und Ableiten nach \(y\) berechnet.
Wird die Stelle \((x_0, y_0)\) nicht spezifiziert, so erhält man pro partieller Ableitung eine Funktion von \(x\) und \(y\) und schreibt z. B. \(\frac{\partial f}{\partial x}(x, y)\) oder kurz \(\frac{\partial f}{\partial x}\).
Bemerkungen:
Für nicht-lineare Funktionen gilt im Allgemeinen \(\Delta z \neq \text{d}z\).
Für lineare Funktionen gilt immer \(\Delta z = \text{d}z\).
Je kleiner \(\text{d}x\) und \(\text{d}y\) umso besser approximiert \(\text{d}z\) den wahren Wert \(\Delta z\).
Schreibweise: Oft wird auch \(\frac{\partial z}{\partial x}\) statt \(\frac{\partial f}{\partial x}\) etc. geschrieben, vgl. \(y'(x)\) statt \(f'(x)\).
Beispiel:
Für \(z = f(x,y) = 3x^2y - y^2\) ist \(\frac{\partial f}{\partial x} = 6xy\) und \(\frac{\partial f}{\partial y} = 3x^2 - 2y\). An der Stelle \((x_0, y_0) = (1,2)\) ergeben sich die Werte \(\frac{\partial f}{\partial x}(1,2) = 12\) und \(\frac{\partial f}{\partial y}(1,2) = -1.\)
Gradient#
An die Stelle der ersten Ableitung \(f'\) im eindimensionalen Fall tritt im zweidimensionalen Fall der Gradient. Der Gradient \(\text{grad}(f)\) ist der Vektor der partiellen Ableitungen. Wir schreiben ihn immer als Spaltenvektor:
Der Gradient an der Stelle \((x_0, y_0)\) ist der Koeffizientenvektor der linearen Approximation \(\text{d}z\) von \(\Delta z\). Die Konturlinien der linearen Approzimation \(\text{d}z\) sind parallele, äquidistante Geraden und der Koeffizientenvektor, also der Gradient, ist orthogonal auf die Konturlinien und zeigt in die Richtung der stärksten Zunahme von \(z\).
weitere Schreibweisen und Begriffe:
Eine andere und ebenfalls übliche Schreibweise für den Gradienten \(\text{grad}(f)\) einer Funktion \(f\) ist \(\nabla f\), wobei \(\nabla\) der sogenannte Nabla-Operator ist:
\[\begin{split}\nabla = \begin{pmatrix}\frac{\partial}{\partial x} \\ \frac{\partial}{\partial y}\end{pmatrix}\end{split}\]Statt z. B. \(\frac{\partial f}{\partial x}\) wird oft die Kurzschreibweise \(f_x\) oder \(f_{|x}\) verwendet.
Statt dem Funktionsnamen wird oft der Name der Outputgröße verwendet und umgekehrt, z. B., \(\text{grad}(z)\) statt \(\text{grad}(f)\) oder \(\text{d}f\) statt \(\text{d}z\).
(Totales) Differential#
Die lineare Approximation \(\text{d}z\) wird als das totale Differential, oder kurz das Differential von \(z\) bezeichnet. Es kann als inneres Produkt des Gradienten mit dem Vektor der Inputgößenänderungen geschrieben werden:
Verallgemeinerung auf den n-dim. Fall#
Die Verallgemeinerung auf eine \(n\)-dimensionale Funktion \(y = f(x_1, x_2, \ldots, x_n)\) ist einfach:
Beispiele#
Beispiel 1: Für \(y(x) = \sin(3x)\) gilt \(\text{d}y = 3\cos(3x)\,\text{d}x\)
Beispiel 2: Für \(z(x,y) = y^2\ln(x)\) gilt \(\text{d}z = \frac{y^2}{x}\,\text{d}x + 2y\ln(x)\,\text{d}y\)
Beispiel 3: Für \(z = f(x,y) = 3x^2y - y^2\) und \((x_0, y_0) = (1,2)\) ergeben sich:
\(\text{grad}(f) = \nabla f = \begin{pmatrix} 6xy \\ 3x^2 - 2y \end{pmatrix}\)
\(\text{grad}(f)(1,2) = \nabla f(1,2) = \begin{pmatrix} 12 \\ -1 \end{pmatrix}\)
\(\text{d}z = 6xy\,\text{d}x + (3x^2 - 2y)\,\text{d}y\)
bei \((1,2)\) ist \(\text{d}z = 12\,\text{d}x - \text{d}y\)
mit zusätzlich \(\text{d}x = 0.1\) und \(\text{d}y = 0.2\):
\(\Delta z = f(1.1, 2.2) - f(1,2) = 1,146\)
\(\text{d}z = 12\cdot 0.1 - 0.2 = 1\)
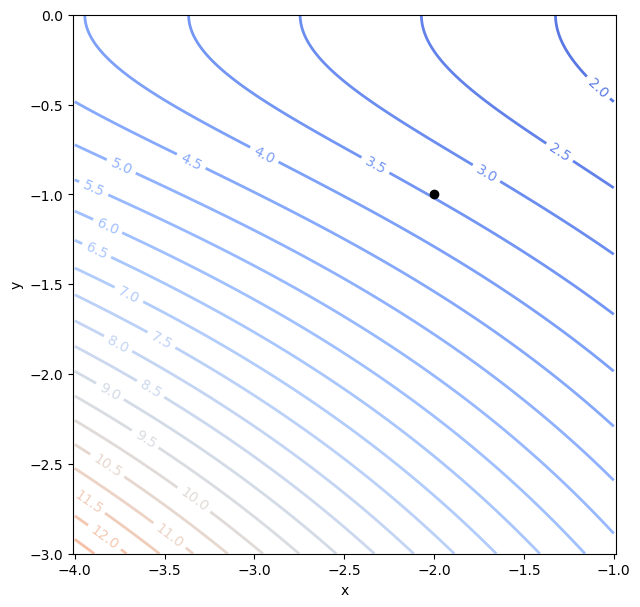
Beispiel 4: \(z = f(x,y) = 0.05(x - 5)^2\sqrt{1 + y^2}\). Zur grafischen Darstellung der Funktion verwenden wir einen Konturplot.
a = 0.05
def f(x, y):
return a*(x - 5)**2*np.sqrt(1 + y**2)
def f_grad(x, y):
return a*2*(x - 5)*np.sqrt(1 + y**2), a*(x - 5)**2*y/np.sqrt(1 + y**2)
x = np.linspace(-4, -1, 200)
y = np.linspace(-3, 0, 200)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
# Stelle:
x0 = -2
y0 = -1
# Konturplot:
plt.figure(figsize=(7,7))
cs = plt.contour(X, Y, Z, np.arange(0, 20, 0.5),
linewidths=2, cmap='coolwarm')
plt.clabel(cs, fontsize=10, fmt='%1.1f')
plt.plot(x0, y0,'o', color='black')
plt.xlabel('x')
plt.ylabel('y')
plt.axis('equal');
# plt.grid(True)
# wahre Differenz:
delta_Z = Z - f(x0, y0)
# Gradient (Vektor der partiellen Ableitungen) an der Stelle:
gx, gy = f_grad(x0, y0)
print(f"Gradient:\n x-Komponente = {gx:.2f}\n y-Komponente = {gy:.2f}")
# totales Differential: linear approximierte Differenz
dX = X - x0
dY = Y - y0
dZ = gx*dX + gy*dY
# Konturplots:
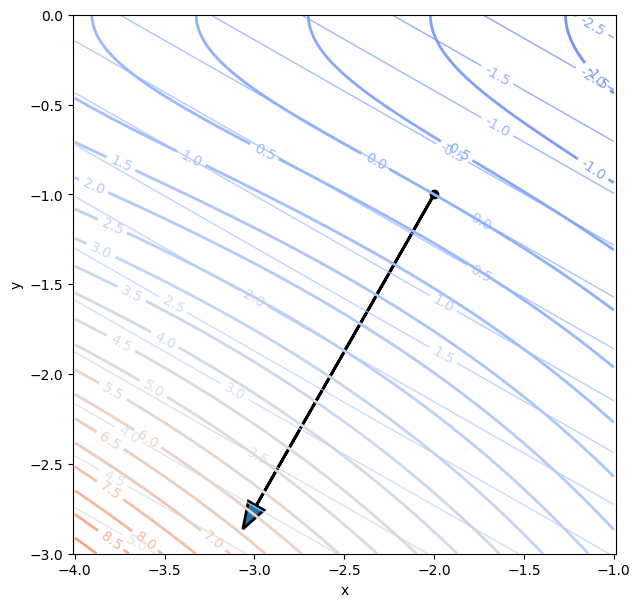
plt.figure(figsize=(7,7))
plt.plot(x0, y0,'ok')
plt.arrow(x0, y0, gx, gy, linewidth=2, head_width=.1)
cs = plt.contour(X, Y, delta_Z, np.arange(-5, 15, 0.5), linewidths=2, cmap='coolwarm')
plt.clabel(cs, fontsize=10, fmt='%1.1f')
cs = plt.contour(X, Y, dZ, np.arange(-5, 15, 0.5), linewidths=1, alpha=0.75, cmap='coolwarm')
plt.clabel(cs, fontsize=10, fmt='%1.1f')
plt.xlabel('x')
plt.ylabel('y')
plt.axis('equal');
# plt.grid(True)
Gradient:
x-Komponente = -0.99
y-Komponente = -1.73
Lineare Fehlerfortpflanzung#
Die folgende Darstellung entstammt dem Buch “Mathematik für Ingenieure und Naturwissenschaftler Band 2” von Lothar Papula:
Das Messergebnis zweier direkt gemessener Größen \(x\) und \(y\) liege in der Form \(x = \bar{x} \pm \Delta x\) und \(y = \bar{y} \pm \Delta y\) vor. Dabei sind \(\bar{x}\) und \(\bar{y}\) die Mittelwerte und \(\Delta x\) und \(\Delta y\) die Messunsicherheiten der beiden Gößen, für die man in diesem Zusammenhang meist die Standardabweichungen der beiden Mittelwerte heranzieht.
Die von den direkten Messgrößen \(x\) und \(y\) abhängige indirekte Messgröße \(z = f(x,y)\) besitzt dann den Mittelwert \(\bar{z} = f(\bar{x},\bar{y})\). Als Genauigkeitsmaß für diesen Mittelwert verwendet man in der linearen Fehlerfortpflanzung die aus dem totalen Differential
berechnete maximale Messunsicherheit
Das Messergebnis für die indirekte Messgröße \(z\) wird in der Form \(z = \bar{z} \pm \Delta z_{\text{max}}\) angegeben.
Beispiel: adaptiert von Papula Band 2, Abschnitt 2.5.5, Beispiel (2) auf Seite 265
Sie produzieren Dosen und können den Radius und die Höhe der als Zylinder modellierten Dosen nur mit folgenden, schlechten Genauigkeiten produzieren: \(r = \bar{r} \pm \Delta r = 10.5 \pm 0.2\) cm und \(h = \bar{h} \pm \Delta h = 15.0 \pm 0.3\) cm. Wie groß ist die daraus abgeleitete Ungenauigkeit der Zylinderoberfläche? Das ist für Sie interessant, da diese direkt mit dem Verbrauch an Dosenblech zusammenhängt.
Antwort: Die Oberfläche des Zylinders hängt mit dessen Radius und Höhe über die Formel \(A(r,h) = 2\pi r^2 + 2\pi rh\) zusammen. Die Lineare Fehlerfortpflanzung liefert
Das Messergebnis für die Oberfläche des Zylinders lautet damit \(A = \bar{A} \pm \Delta A_{\text{max}} = 1682.32 \pm 65.03\). Der prozentuale Maximalfehler beträgt \(\left\vert \frac{\Delta A_{\text{max}}}{\bar{A}} \right\vert = \frac{65.03}{1682.32} \simeq 0.039 = 3.9\,\%\).
Nicht-lineare Optimierung#
Höhere partielle Ableitungen#
Die erste partielle Ableitung einer Funktion \(f(x_1, \ldots, x_n)\) nach der Inputvariablen \(x_k\) liefert die Funktion \(\frac{\partial f}{\partial x_k}(x_1, \ldots, x_n)\), kurz \(\frac{\partial f}{\partial x_k}\). Diese kann wiederum partiell abgeleitet werden, z. B. nach der Inputvariablen \(x_l\). Das liefert die Funktion \(\frac{\partial^2 f}{\partial x_l\partial x_k}(x_1, \ldots, x_n)\), kurz \(\frac{\partial^2 f}{\partial x_l\partial x_k}\), eine partielle Ableitung zweiter Ordnung. Die Funktion \(f(x_1, \ldots, x_n)\) hat \(n\) Inputvariablen und somit \(n^2\) partielle Ableitungen zweiter Ordnung.
Die zweifache Ableitung nach der selben Inputvariablen \(x_k\) wird statt \(\frac{\partial^2 f}{\partial x_k\partial x_k}\) meist \(\frac{\partial^2 f}{\partial x_k^2}\) geschrieben.
Partielle Ableitungen höherer als zweiter Ordnung werden analog durch wiederholtes partielles Ableiten berechnet.
Es gilt für in der Praxis typische Funktionen, dass
\[\frac{\partial^2 f}{\partial x_l\partial x_k} = \frac{\partial^2 f}{\partial x_k\partial x_l}.\]
Hessematrix:
Die \(n^2\) partiellen Ableitungen zweiter Ordnung einer Funktion \(f(x_1, \ldots, x_n)\) werden in der sogenannten Hessematrix \(H(x_1, \ldots, x_n)\), kurz \(H\), angeordnet:
Beispiel: \(z = f(x,y) = 3x^2y\)
\(\frac{\partial f}{\partial x} = 6xy\), \(\frac{\partial^2 f}{\partial x^2} = 6y\), \(\frac{\partial^2 f}{\partial y\partial x} = 6x\)
\(\frac{\partial f}{\partial y} = 3x^2\), \(\frac{\partial^2 f}{\partial y^2} = 0\), \(\frac{\partial^2 f}{\partial x\partial y} = 6x\)
\(\text{grad}(f) = \nabla f = \begin{pmatrix} 6xy \\ 3x^2\end{pmatrix}\)
\(H = \begin{pmatrix} 6y & 6x \\ 6x & 0\end{pmatrix}\)
Nicht-lineare Optimierung ohne Nebenbedingungen#
Problemtyp: Min. oder Max. \(f(x_1, x_2, \ldots, x_n)\)
Wiederholung des 1-dimensionalen Falls:
Notwendige Bedingung: Eine Funktion \(f(x)\), die an einer Stelle \(x_0\) ein lokales Optimum (lokales Minimum oder lokales Maximum, allgemein einen Extremwert) hat, muss das Optimalitätskriterium \(f'(x_0) = 0\) erfüllen.
Hinreichende Bedingung: Umgekehrt gilt:
Wenn \(f'(x_0) = 0\) und \(f''(x_0) > 0\), dann hat \(f\) bei \(x_0\) ein lokales Minimum.
Wenn \(f'(x_0) = 0\) und \(f''(x_0) < 0\), dann hat \(f\) bei \(x_0\) ein lokales Maximum.
Verallgemeinerung auf den \(n\)-dimensionalen Fall:
Wir betrachten zunächst eine Funktion \(z=f(x,y)\) von zwei Variablen \(x\) und \(y\). An die Stelle der ersten Ableitung \(f'(x_0)\) tritt der Gradient \(\nabla f(x_0,y_0)\). Die Bedingung \(\nabla f(x_0, y_0)=0\) ist eine Vektorgleichung und bedeutet auf Komponentenebene, dass jede partielle Ableitung von \(f\) bei \(x_0\) Null ist. An die Stelle der zweiten Ableitung \(f''(x_0)\) tritt die Hessematrix \(H(x_0,y_0)\). Die Bedingung der Positivität \(H(x_0,y_0)>0\) bzw. der Negativität \(H(x_0,y_0)<0\) ist aber keine komponentenweise Matrixungleichung! Vielmehr ist folgendes gemeint:
\(H(x_0,y_0) > 0\) bedeutet, dass alle Eigenwerte von \(H(x_0,y_0)\) größer Null sind. In diesem Fall heißt die Hessematrix positiv definit.
\(H(x_0,y_0) \geq 0\) bedeutet, dass alle Eigenwerte von \(H(x_0,y_0)\) größer oder gleich Null sind. In diesem Fall heißt die Hessematrix positiv semidefinit.
\(H(x_0,y_0) \leq 0\) bedeutet, dass alle Eigenwerte von \(H(x_0,y_0)\) kleiner oder gleich Null sind. In diesem Fall heißt die Hessematrix negativ semidefinit.
\(H(x_0,y_0) < 0\) bedeutet, dass alle Eigenwerte von \(H(x_0,y_0)\) kleiner Null sind. In diesem Fall heißt die Hessematrix negativ definit.
Was die Eigenwerte einer Matrix sind und wie man sie von Hand berechnet, wird erst im nächsten Semester unterrichtet. Wir verwenden sie trotzdem und verwenden den Befehl eig für ihre Berechnung. Hier ein Beispiel:
H = np.array([[4, 2],
[2, 1]])
L, V = np.linalg.eig(H)
for l in L:
print(f"{l} ist ein Eigenwert von H.")
print("Die Matrix H ist daher positiv semidefinit.")
5.0 ist ein Eigenwert von H.
0.0 ist ein Eigenwert von H.
Die Matrix H ist daher positiv semidefinit.
Die Optimalitätskriterien für den zweidimensionalen Fall lauten:
Notwendige Bedingung: Falls die Funktion \(f(x,y)\) bei \((x_0,y_0)\) ein lokales Minimum (Maximum) hat, dann ist \(\nabla f(x_0,y_0)=0\) und \(H(x_0,y_0)\) positiv semidefinit (negativ semidefinit).
Hinreichende Bedingung: Falls \(\nabla f(x_0,y_0)=0\) und \(H(x_0,y_0)\) positiv definit (negativ definit) ist, dann hat \(f\) bei \((x_0,y_0)\) ein lokales Minimum (Maximum).
Die Verallgemeinerung auf eine \(n\)-dimensionale Funktion \(y = f(x_1, x_2, \ldots, x_n)\) führt auf die Bedingungen, dass der Gradient Null ist und die \(n\times n\) Hessematrix positiv (semi)definit bzw. negativ (semi)definit ist. Eine Stelle, an der der Gradient von \(f\) Null ist, heißt kritischer Punkt. An einem kritischen Punkt ist somit auch das Differential Null (\(\text{d}f=0\)), und die Tangential(hyper)ebene ist waagrecht.
Nicht-lineare Optimierung mit Nebenbedingungen#
Problemtyp: Min. oder Max. \(f(x_1, x_2, \ldots, x_n)\) unter der Nebenbedingung \(g(x_1, x_2, \ldots, x_n) = 0\)
Wir beginnen mit einem Beispiel, das wir zunächst als Extremwertsaufgabe wie in der Schule und anschließend mit der Methode der Lagrange-Multiplikatoren lösen. Der Vorteil der letzteren Methode ist, dass sie sich auf beliebige Dimensionen und mehrere Nebenbedingungen problemlos verallgemeinern läßt.
Beispiel: Man finde jenes Rechteck mit Umfang \(u=12\), das maximalen Flächeninhalt hat, d. h. für \(x\) und \(y\) die Länge und die Breite des Rechtecks maximiere \(f(x,y)=xy\) unter der Nebenbedingung \(g(x,y) = 2x + 2y -12 =0\).
erster Lösungsweg: Die Nebenbedingung läßt sich nach einer Variablen auflösen, z. B. \(y = 6 - x\), sodass die Zielfunktion nach dem Einsetzen nur noch von einer Variablen abhängt: \(f(x, 6 - x) = x(6 - x) = 6x - x^2\). Man erhält ein 1-dimensionales Optimierungsproblem ohne Nebenbedingungen: Max. \(6x - x^2\). Nullsetzen der ersten Ableitung liefert \(6 - 2x =0\) und die Lösung \(x^*=3,\) \(y^*=6 - 3 = 3 = x^*\), also ein Quadrat. Die maximale Fläche ist \(f(x^*, y^*)=9\). Die zweite Ableitung ist -2, also kleiner Null. Daher ist die Lösung ein lokales (und in diesem Fall auch globales) Maximum.
zweiter Lösungsweg: Methode der Lagrange-Multiplikatoren:
Wir zeichnen die Konturlinien der Zielfunktion \(f(x,y)=xy\), die Nebenbedingung \(g(x,y) = 2x + 2y - 12 = 0\) und die Gradienten \(\nabla f\) und \(\nabla g\) an der optimalen Stelle \((3,3)\).
x = np.linspace(0, 10, 200)
y = np.linspace(0, 10, 200)
X, Y = np.meshgrid(x, y)
F = X*Y
G = 2*X + 2*Y - 12
# Konturplot:
plt.figure(figsize=(7,7))
cs = plt.contour(X, Y, F, np.arange(1, 60, 2), linewidths=2, cmap='coolwarm')
plt.clabel(cs, fontsize=10, fmt='%1.1f')
cs = plt.contour(X, Y, G, 0, linewidths=2, colors='black')
plt.plot(3,3, 'og')
plt.arrow(3,3, 2,2, linewidth = 3, color='black', head_width=0.2)
plt.arrow(3,3, 3,3, linewidth = 2, color='red', head_width=0.2, alpha=0.75)
plt.xlabel('x')
plt.ylabel('y')
plt.axis('equal')
plt.grid(True)
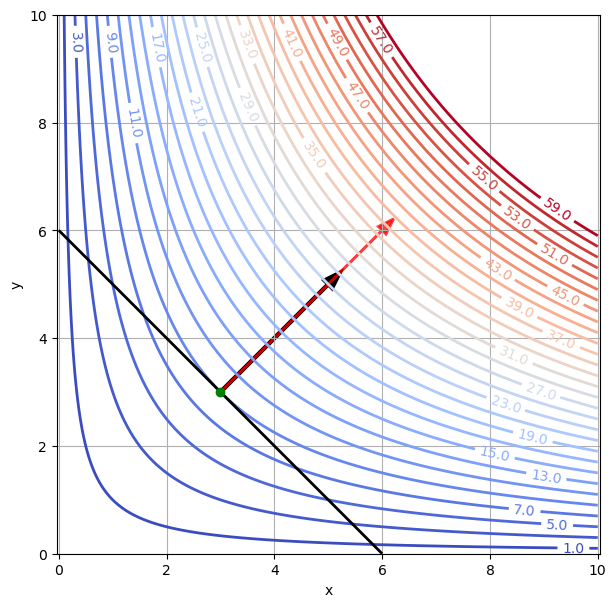
Der Gradient der Zielfunktion \(f\) und der Gradient der Nebenbedingungsfunktion \(g\) sind im Optimum kollinear, d. h. linear abhängig oder anders ausgedrückt ein Vielfaches von einander:
mit Vielfachem \(\lambda\). Wenn wir diese Bedingung als Ausgangspunkt zur Berechnung der Lösung verwenden, dann lautet sie
Daraus folgt \(x= y\), was eingesetzt in die Nebenbedingung die selbe Lösung \(x^*=3\), \(y^*=3\) liefert.
Methode der Lagrange-Multiplikatoren allgemein:
Falls die Zielfunktion \(f(x_1, x_2, \ldots, x_n)\) unter den Nebenbedingungen
ein lokales Optimum bei \(x^* =(x_1^*, x_2^*, \ldots, x_n^*)\) hat, dann gibt es Lagrange-Multiplikatoren \(\lambda_1, \lambda_2, \ldots, \lambda_m,\) sodass gilt:

