Lösungen#

Python-Pakete#

import numpy as np
import matplotlib.pyplot as plt
import math

Aufgabe 1: Ableiten#

Berechnen Sie die Ableitung von folgenden Funktionen.

$f(x) = 4\sqrt[3]{x^5} - 4e^x + \sin(x)$
$f(x) = 2x^2\ln(x)$
$f(x) = \dfrac{10x}{x^2 + 1}$
$f(x) = 3e^{-4x}$
$f(x) = \sin^2(2x - 4)$
$f(t) = \sin(\omega t)$ (erste und zweite Ableitung)

Lösung#

$f'(x) = \frac{20}{3}\sqrt[3]{x^2} - 4e^x + \cos(x)$
$f'(x) = 4x\ln(x) + 2x$
$f'(x) = \dfrac{10(1-x^2)}{(x^2 + 1)^2}$
$f'(x) = -12e^{-4x}$
$f'(x) = 4\sin(2x - 4)\cos(2x - 4)$
$f'(x) = \omega\cos(\omega t)$ und $f''(t) = -\omega^2\sin(\omega t)$

Aufgabe 2: Differenzieren, Tangente#

Differenzieren Sie die Funktion $f(x) = \cos(2-x) + 3e^{-x} - \frac{1-x}{x^2}$.
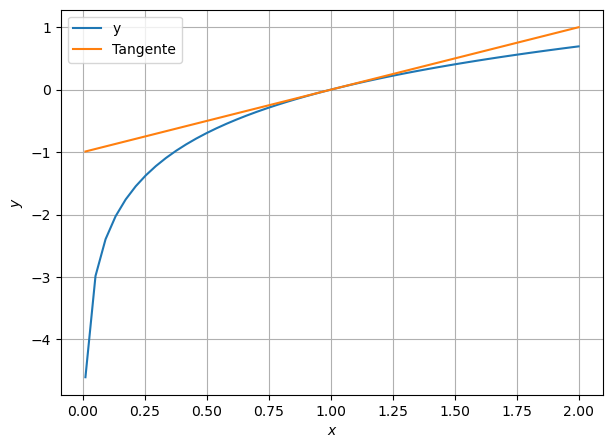
Bestimmen Sie die Tangente an die Funktion $y=\ln(x)$ bei $x=1$, und plotten Sie Funktion und Tangente am Computer.

Lösung#

$f'(x) = \sin(2 - x) - 3e^{-x} - \frac{x - 2}{x^3}$
$y_{\text{Tang.}} = x - 1$

x = np.linspace(0.01, 2)
y = np.log(x)
y_tang = x - 1

plt.figure(figsize=(7, 5))
plt.plot(x, y, label='y')
plt.plot(x, y_tang, label='Tangente')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend()
plt.grid(True)

Aufgabe 3: Tangentengleichung#

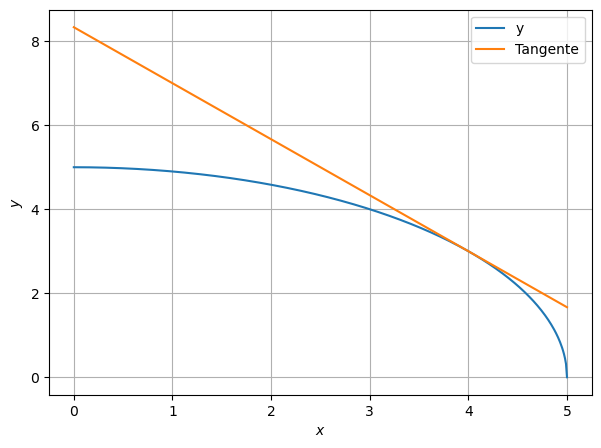
Gegeben ist die Funktion $y = \sqrt{25 - x^2}$.

Bestimmen Sie die Gleichung der Tangente an der Stelle $x_0 = 4$.
Erstellen Sie einen Plot der Graphen der Funktion und der Tangente am Computer.

Lösung#

$y_{\text{Tang.}} = -\frac{4}{3}x + \frac{25}{3}$

x = np.linspace(0, 5, num=500)
y = np.sqrt(25 - x**2)
y_tang = -4/3*x + 25/3

plt.figure(figsize=(7, 5))
plt.plot(x, y, label='y')
plt.plot(x, y_tang, label='Tangente')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend()
plt.grid(True)

Aufgabe 4: Differenzieren, Extrema#

Differenzieren Sie die Funktion $f(x) = e^{5-x} + 3\cos^2(x)$.
Berechnen Sie alle Extrema (Maxima und Minima) der Funktion $f(x) = -8x^3 + 12x^2 +18x$.

Lösung#

$f'(x) = -e^{5-x} - 6\cos(x)\sin(x)$
$f''(x) = -48x + 24$, lokales Maximum bei $x=1.5$ und lokales Minimum bei $x=-0.5$

print(-48*1.5 + 24)
print(-48*(-.5) + 24)

-48.0
48.0

Aufgabe 5: Kurvendiskussion#

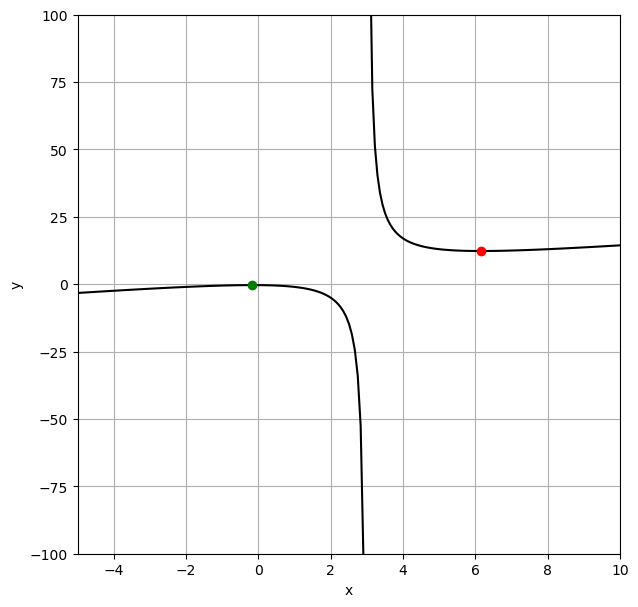
Plotten Sie den Graphen der Funktion $y = \dfrac{x^2+1}{x-3}$ am Computer, und bestimmen Sie die maximale Definitionsmenge, Nullstellen, Pole, Maxima und Minima.

Lösung#

Die maximale Definitionsmenge besteht aus allen reellen Zahlen außer dem Pol $x=3$, keine Nullstellen, lokales Maximum bei $x=-0.162$, lokales Minimum bei $x=6.162$.

plt.figure(figsize=(7,7))

def f(x):
    return (x**2 + 1)/(x - 3)

x = np.linspace(-5, 2.99, 100)
plt.plot(x, f(x), 'k')
x = np.linspace(3.01, 10, 100)
plt.plot(x, f(x), 'k')

x_1 = 3 + np.sqrt(10)
x_2 = 3 - np.sqrt(10)
plt.plot(x_1, f(x_1), 'ro')
plt.plot(x_2, f(x_2), 'go')

plt.ylim(-100, 100)
plt.xlim(-5, 10)
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)

print(f"lokales Minimum bei x= {3 + np.sqrt(10):6.3f}")
print(f"lokales Maximum bei x= {3 - np.sqrt(10):6.3f}")

lokales Minimum bei x=  6.162
lokales Maximum bei x= -0.162

Aufgabe 6: Extremwerte#

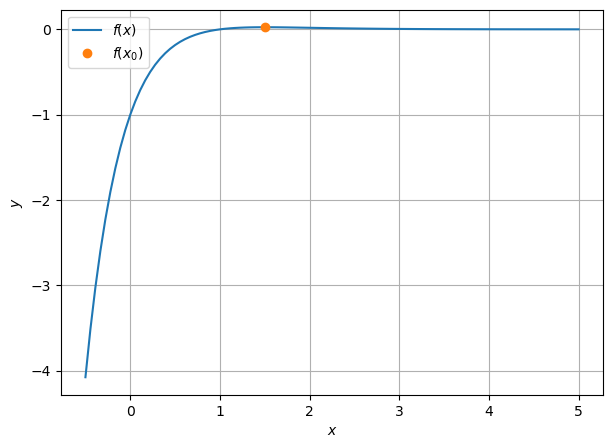
Bestimmen Sie die Extremwerte der Funktion $f(x) = (x-1)e^{-2x}$. Handelt es sich um Maximum, Minimum oder Sattelpunkt? Erstellen Sie einen Plot der Funktion am Computer.

Lösung#

Maximum bei $x=1.5$

x = np.linspace(-0.5, 5, 100)
f = lambda x: (x - 1)*np.exp(-2*x)
x_0 = 1.5

plt.figure(figsize=(7, 5))
plt.plot(x, f(x), label='$f(x)$')
plt.plot(x_0, f(x_0), 'o', label='$f(x_0)$')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend()
plt.grid(True)
plt.grid(True)

Aufgabe 7: maximale Bremskraft#

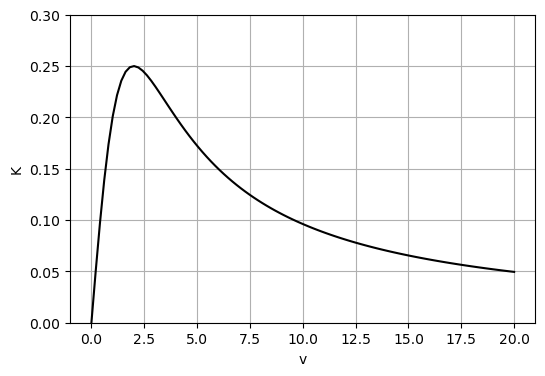
Die Bremskraft einer Scheibenbremse ist gegeben durch $K(v)=\dfrac{a^2v}{v^2 + b^2}$, wobei $v > 0$ die Geschwindigkeit der Scheibe angibt und $a > 0$ und $b > 0$ Konstanten sind.

Skizzieren Sie den Graphen von $K$ ohne eine Wertetabelle zu verwenden. Plotten Sie anschließend den Graphen am Computer.
Bei welcher Geschwindigkeit ist die Bremskraft maximal?
Berechnen Sie die maximale Bremskraft.

Lösung#

Quelle: Papula, Lothar (2018): Mathematik für Ingenieure und Naturwissenschaftler Band 1: Ein Lehr- und Arbeitsbuch für das Grundstudium. Seite 420.

Siehe Abbildung mit $a=1$ and $b=2$.
$v=b$
$K(b)=\frac{a^2}{2b}$

a = 1
b = 2

v = np.linspace(0, 20, 100)
K = a**2*v/(v**2 + b**2)

plt.figure(figsize=(6, 4))
plt.plot(v, K, 'k')
plt.ylim(0, 0.3)
plt.xlabel('v')
plt.ylabel('K')
plt.grid(True)

Aufgabe 8: kleinster Abstand von Massenpunkten#

Zwei Massenpunkte A und B bewegen sich entlang der beiden Koordinatenachsen mit den Geschwindigkeiten $v_A = 0.5$ m/s und $v_B = 0.6$ m/s in die Richtung des Koordinatenursprungs. Zu Beginn zum Zeitpunkt $t=0$ sind sie an den Orten $x_A(0) = 15\text{ m}$ und $y_B(0) = 12\text{ m}$. Nach welcher Zeit ist ihr Abstand am kleinsten?

Lösung#

Zur Zeit $t=24.1$ bei einem Abstand von $3.84$.

(15 + 12*1.2)/1.22

24.098360655737704

Aufgabe 9: periodische Extremwerte#

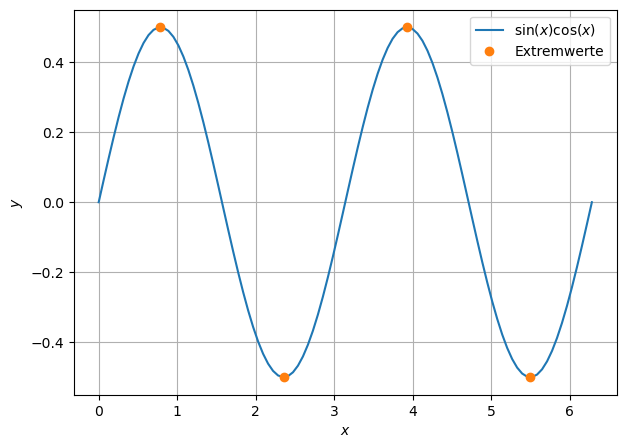
Wo besitzt $f(x)=\sin(x)\cos(x)$ Extremwerte im Bereich $[0, 2\pi]$? Begründen Sie Ihre Antwort durch eine Rechnung. Erstellen Sie einen Plot der Funktion am Computer.

Lösung#

Lösungen in [0, 2$\pi$]: $x = \frac{\pi}{4} + k \frac{\pi}{2}$ für $k= 0,1,2,3$

x   = np.linspace(0, 2*np.pi, 100)
x_e = np.array([np.pi/4 + k*np.pi/2 for k in range(4)])

plt.figure(figsize=(7, 5))
plt.plot(x, np.sin(x)*np.cos(x), label='$\sin(x)\cos(x)$')
plt.plot(x_e, np.sin(x_e)*np.cos(x_e), 'o', label='Extremwerte')
plt.xlabel('$x$')
plt.ylabel('$y$')
plt.legend()
plt.grid(True)
plt.show()

Aufgabe 10: Taylor-Reihen#

Berechnen Sie die Taylor-Reihen bis zur zweiten Ordnung von

$f(x) = \cos(x)$ at $x_0 = \frac{\pi}{3}$
$f(x) = \sqrt{x}$ at $x_0 = 1$

Lösung#

$f(x) = \cos(x) = \frac{1}{2} - \frac{\sqrt{3}}{2}(x - \frac{\pi}{3}) - \frac{1}{4}(x - \frac{\pi}{3})^2 + \cdots$
$f(x) = \sqrt{x} = 1 + \frac{1}{2}(x - 1) - \frac{1}{8}(x - 1)^2 + \cdots$

Aufgabe 11: Taylor-Reihe des Kehrwerts#

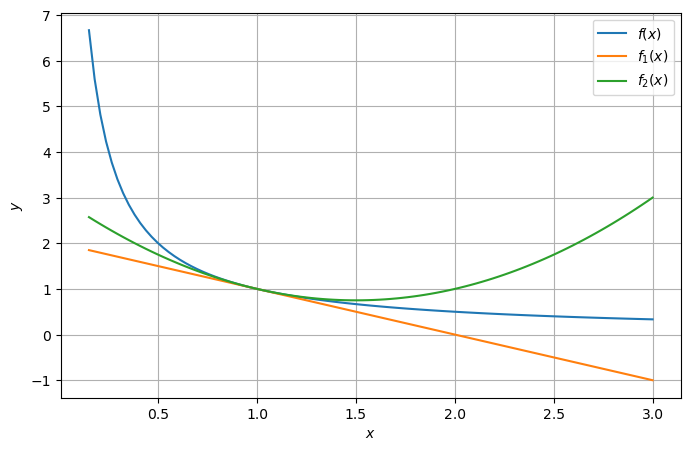
Berechnen Sie von $f(x) = \frac{1}{x}$ bei $x_0 = 1$ die Taylor-Reihe bis zur zweiten Ordnung, und stellen Sie Ihr Ergebnis am Computer grafisch dar.

Lösung#

\[\begin{split}\begin{align} f_{\text{Parab.}}(x) &= f(x_0) + f'(x_0)(x - x_0) + \frac{1}{2}f''(x_0)(x - x_0)^2 \\ &= 1 - (x - 1) + (x - 1)^2 \\ &= 3 - 3x + x^2 \end{align}\end{split}\]

x = np.linspace(0.15, 3, num=100)
f   = lambda x: 1/x              # Ausgangsfunktion
f_1 = lambda x: 2 - x            # Taylor-Reihe bis 1. Ordnung = Tangente
f_2 = lambda x: 3 - 3*x + x**2   # Taylor-Reihe bis 2. Ordnung = Parabel

plt.figure(figsize=(8, 5))
plt.plot(x, f(x),   label="$f  (x)$")
plt.plot(x, f_1(x), label="$f_1(x)$")
plt.plot(x, f_2(x), label="$f_2(x)$")
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.legend()
plt.grid(True)

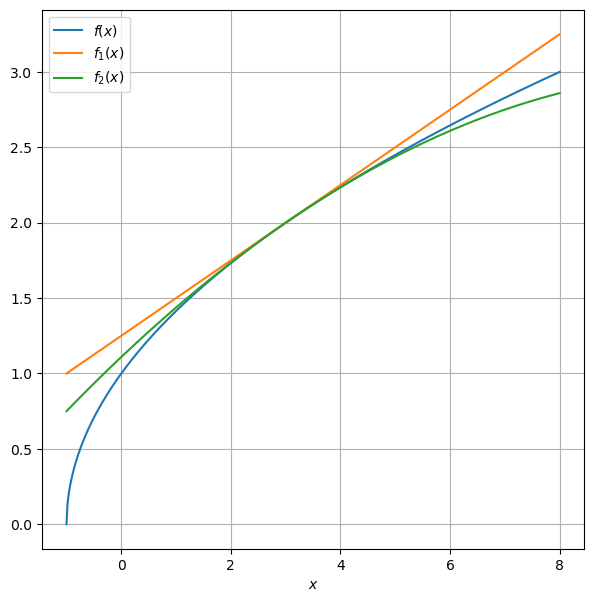
Aufgabe 12: Taylor-Reihe einer Wurzelfunktion#

Berechnen Sie von $f(x) = \sqrt{1 + x}$ bei $x_0 = 3$ die Taylor-Reihe bis zur zweiten Ordnung, und stellen Sie Ihr Ergebnis am Computer grafisch dar.

Lösung#

\[\begin{split}\begin{align} f_{\text{Parab.}}(x) &= f(x_0) + f'(x_0)(x - x_0) + \frac{1}{2}f''(x_0)(x - x_0)^2 \\ &= 2 + \frac{1}{4}(x - 3) - \frac{1}{64}(x - 3)^2 \end{align}\end{split}\]

x = np.linspace(-1, 8, num=500)
f   = lambda x: np.sqrt(1 + x)
f_1 = lambda x: 2 + 1/4*(x - 3)
f_2 = lambda x: 2 + 1/4*(x - 3) - 1/64*(x - 3)**2

plt.figure(figsize=(7,7))
plt.plot(x, f(x),   label="$f  (x)$")
plt.plot(x, f_1(x), label="$f_1(x)$")
plt.plot(x, f_2(x), label="$f_2(x)$")
plt.xlabel("$x$")
plt.legend()
plt.grid(True)

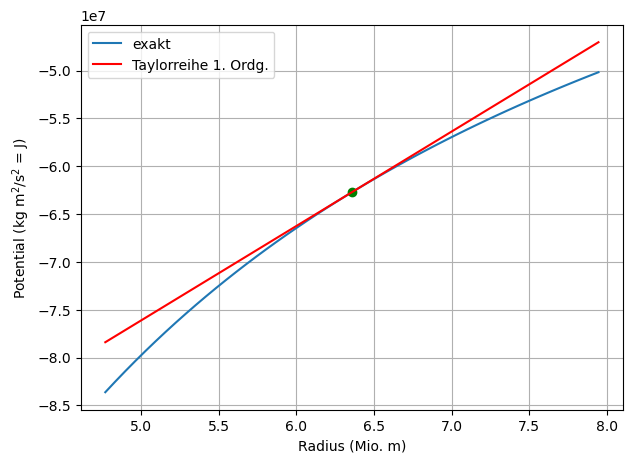
Aufgabe 13: Taylorreihe des Gravitationalspotentials#

Berechnen Sie die Taylorreihe des Gravitationspotentials $\phi(r) = -G\frac{mM_E}{r}$ eines Körpers der Masse $m$ an der Erdoberfläche bis zur ersten Ordnung.
Vergleichen Sie Ihr Ergebnis mit der bekannten Formel $mgh$, wobei $g=9.81\frac{m}{s^2}$ die Erdbeschleunigung und $h$ die Höhe über der Erdoberfläche sind.
Erstellen Sie einen Plot des wahren und approximierten Graviationspotentials in der Nähe der Erdoberfläche am Computer.

Daten: Gravitationskonstante $G = 6{,}6742\cdot10^{-11}\;\mathrm{\frac{m^3}{kg\,s^2}}$, Masse der Erde $M_E = 5{,}974\cdot10^{24}\;\mathrm{kg}$, Durchmesser der Erde $d= 12714$ km

Lösung#

Taylorreihe bis 1. Ordnung: $\phi(r_E + h) \simeq \phi(r_E) + \phi'(r_E)h = -G\frac{mM_E}{r_E} + G\frac{mM_E}{r_E^2}h$
Der erste Term ist eine Konstante und daher für die potentielle Energie irrelevant. Wir vergleichen den zweite Term $G\frac{mM_E}{r_E^2}h$ mit $mgh$. Der Term $G\frac{M_E}{r_E^2}$ hat einen Wert von $9.87\frac{m}{s^2}$ und ist somit vergleichbar mit $g=9.81\frac{m}{s^2}$.
Siehe Code.

G  = 6.6742e-11   # m^3/(kg*s)
ME = 5.974e24     # kg
rE = 12714.0e3/2  # m
g = G*ME/rE**2    # m/s^2

print(f"{rE = :.3f} m")
print(f"{g  = :.3f} m/s^2")

rE = 6357000.000 m
g  = 9.866 m/s^2

m = 1
r = np.linspace(rE*0.75, rE*1.25)

plt.figure(figsize=(7,5))
plt.plot(r/1e6, -G*m*ME/r, label='exakt')
plt.plot(rE/1e6, -G*m*ME/rE, 'go')
plt.plot(r/1e6, -G*m*ME/rE + g*m*(r - rE), 'r', label='Taylorreihe 1. Ordg.')
plt.legend(loc='best')
plt.xlabel('Radius (Mio. m)')
plt.ylabel('Potential (kg m$^2$/s$^2$ = J)')
plt.grid(True)

Aufgabe 14: Differentialquotient und Ableitungsregeln#

Leiten Sie die Funktion $f(x)=x^{n}$ an der Stelle $a$ mit Hilfe des Differentialquotienten ab.
Leiten Sie die Funktion $f(x)=x^{n}$ an der Stelle $a$ mit Hilfe der Ableitungsregeln ab.

Hinweise: siehe Binomische Formeln

\[(x^{n}-a^{n})=(x-a)\sum_{k=1}^{n}x^{n-k}a^{k-1}\]

\[f^{\prime}(a) = \lim_{x \to a}\frac{f(x)-f(a)}{x-a}\]

Lösung#

ad 1.:

\[\begin{split}\begin{align} f^{\prime}(a) &= \lim_{x \to a}\frac{f(x)-f(a)}{x-a}\\ f^{\prime}(a) &= \lim_{x \to a}\frac{x^{n}-a^{n}}{x-a}\\ f^{\prime}(a) &= \lim_{x \to a}\frac{(x-a)\sum_{k=1}^{n}x^{n-k}a^{k-1}}{x-a}\\ f^{\prime}(a) &= \lim_{x \to a}\sum_{k=1}^{n}x^{n-k}a^{k-1}\\ f^{\prime}(a) &= \sum_{i=1}^{n}a^{n-k}a^{k-1}\\ f^{\prime}(a) &= \sum_{i=1}^{n}a^{n-1}\\ f^{\prime}(a) &= na^{n-1} \end{align}\end{split}\]

ad 2.:

\[\begin{split}\begin{align} f^{\prime}(x) &=nx^{n-1}\\ f^{\prime}(a) &=na^{n-1} \end{align}\end{split}\]

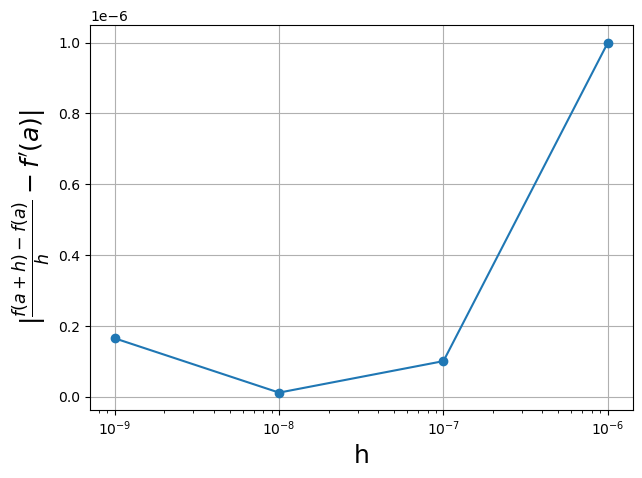
Aufgabe 15: Differenzenquotient#

Approximieren Sie für die Funktion $f(x)=x^2$ an der Stelle $a = 1$ den Differentialquotienten durch den Differenzenquotienten.

Verwenden Sie unterschiedliche Schrittweiten $h=x-a$ die Werte $10^{-6},...,10^{-9}$, und vergleichen Sie die Werte der Approximationen mit dem exakten Wert $f^{\prime}(a)$.
Plotten Sie den Fehler $\left|\frac{f(a+h) - f(a)}{h} - f^{\prime}(1)\right|$ gegen die logarithmischen Schrittweiten $\log_{10}(h)$. Was beobachten Sie? Welche Schrittweite $h$ ergibt den kleinsten Fehler?

Lösung#

h_list = [10**-i for i in range(6,10)]
exact_value = 2

error_list = []
for h in h_list:
    error_list.append(np.abs(exact_value - ((1 + h)**2 - (1)**2)/h))

plt.figure(figsize=(7, 5))
plt.semilogx(h_list, error_list, '-o')
plt.grid()
plt.xlabel("h", fontsize=18)
plt.ylabel(r"$|\frac{f(a+h)-f(a)}{h}-f^{\prime}(a)|$", fontsize=18) 
# the r makes the string a raw string (literal). 
# This is necessary because \ is no valid string literal.

print(f"Beste Wahl für h: {np.sqrt(np.finfo(float).eps)}") 
# Aus der Theorie für die Aufgabe ist 10^(-8) ausreichend

Beste Wahl für h: 1.4901161193847656e-08

Aufgabe 16: Minimaler Abfall#

Aus einem Baumstamm mit kreisförmigem Querschnitt soll ein Balken mit rechteckigem Querschnitt gefertigt werden, und zwar so, dass möglichst wenig Abfall entsteht. Formulieren Sie die Aufgabe mathematisch, und bestimmen den Sie den optimalen Querschitt.

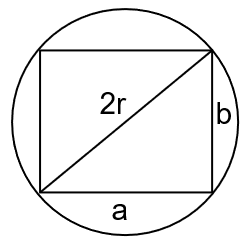
Hinweis: Maximieren Sie die Fläche des Rechtecks, die innerhalb des kreisförmigen Querschnitts liegt.

Lösung#

\[\begin{split}\begin{align} A_{Kreis}&=\pi r^2\\ A_{Rechteck} &= ab\\ 2r&=\sqrt{a^2+b^2}\\ a&=\sqrt{4r^2-b^2}\\ A_{Rechteck} &= \sqrt{4r^2-b^2}b=\sqrt{4r^2b^2-b^4}\\ \frac{dA_{Rechteck}}{db}&=\frac{8r^2b-4b^3}{2\sqrt{4r^2b^2-b^4}}=0\\ 8r^2b&=4b^3\\ b=\sqrt{2r^2}\\ \frac{d^2A_{Rechteck}}{db^2}\Big|_{b=\sqrt{2r^2}}&=-10\\ a&=\sqrt{4r^2-2r^2}=\sqrt{2r^2} \end{align}\end{split}\]

Aufgabe 17: Rinne mit maximalem Fassungsvermögen#

Aus drei Brettern, die alle die Breite $g$ haben, soll eine Rinne mit maximalem Fassungsvermögen gebaut werden.

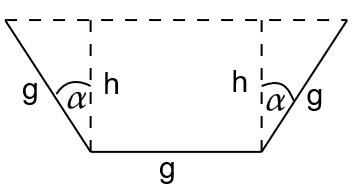
Formulieren Sie die Aufgabe mathematisch, und bestimmen Sie den Winkel $\alpha \in [0,\frac{\pi}{2})$ für maximales Fassungsvermögen

analytisch,
grafisch am Computer,
numerisch am Computer.

Hinweise:

Die linke und rechte Teilfäche ist jeweils gleich $\frac{1}{2}gh\sin(\alpha)$. Schreiben Sie $h$ in Abhängigkeit von $g$ und dem Winkel $\alpha$.
Formel für den Kosinus des doppelten Winkels: $\cos(2x) = 1 - 2\sin^2(x)$
To find a root of a scalar function you can use root_scalar.

Lösung#

\[\begin{split}\begin{align} A &= 2 \left( \frac{1}{2}gh\sin(\alpha) \right) + gh = g \left( h + h\sin(\alpha) \right) \\ h &= g\cos(\alpha) \\ A &= g^2 \left( \cos(\alpha) + \cos(\alpha)\sin(\alpha) \right) \\ A &= g^2 \left( \cos(\alpha)+\frac{1}{2}sin(2\alpha) \right) \\ \frac{dA}{d\alpha} &= g^2 (-\sin(\alpha) + \cos(2\alpha) ) = 0\\ \sin(\alpha) &= \cos(2\alpha) \\ \sin(\alpha) &= 1 - 2\sin^2(\alpha)\\ \sin^2(\alpha) + \frac{1}{2}\sin(\alpha) - \frac{1}{2} &= 0 \end{align}\end{split}\]

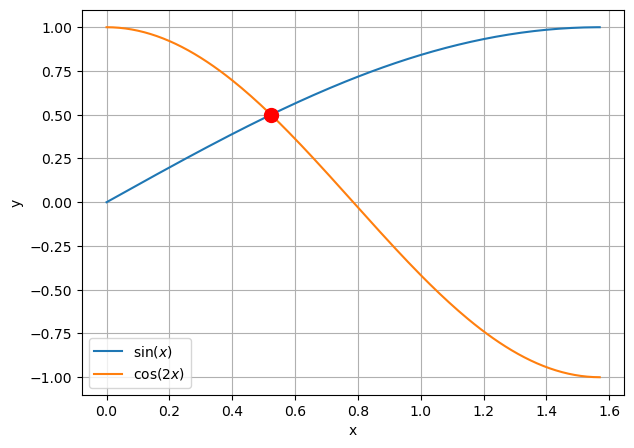
Die quadratische Gleichung hat die Lösungen $\sin(\alpha_1) = \frac{1}{2}$ und $\sin(\alpha_2) = -1$, d. h. Die einzige für das Beispiel relevante Lösung ist $\alpha = \frac{\pi}{6}$.

x = np.arange(0, np.pi/2, 10**(-2))
y_1 = np.sin(x)
y_2 = np.cos(2*x)

plt.figure(figsize=(7, 5))
plt.plot(x, y_1, label=r"$\sin(x)$")
plt.plot(x, y_2, label=r"$\cos(2x)$")
plt.plot(np.pi/6, np.sin(np.pi/6), "or", markersize=10) # Schnittpunkt der Funktionen bei pi/6
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
plt.grid()

print(f"Schnittpunkt bei pi/6 = {np.pi/6:.6f}")

Schnittpunkt bei pi/6 = 0.523599

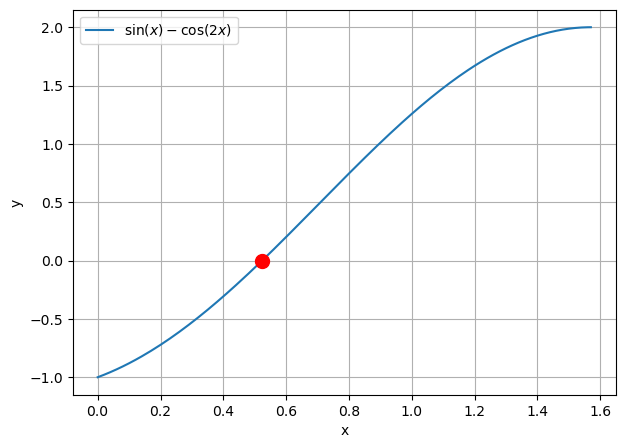
plt.figure(figsize=(7, 5))
plt.plot(x, y_1 - y_2, label=r"$\sin(x) - \cos(2x)$")
plt.plot(np.pi/6, 0, "or", markersize=10)  # Nullstelle bei pi/6
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
plt.grid()

print(f"Nullstelle bei pi/6 = {np.pi/6:.6f}")

Nullstelle bei pi/6 = 0.523599

from scipy import optimize

def f(x):
    return np.sin(x) - np.cos(2*x)

sol = optimize.root_scalar(f, bracket=[0, np.pi/2], method='brentq')
print(f"Nullstelle bei {sol.root:.6f}")

Nullstelle bei 0.523599

Aufgabe 18: Quadratische Gleichung via Differentialrechnung und Verschiebungen#

Eine Möglichkeit, die $p$-$q$ Formel der quadratischen Gleichung herzuleiten, ist über die Differentialrechnung. Gegeben sei die Funktion

\[f(x)=x^2+px+q\]

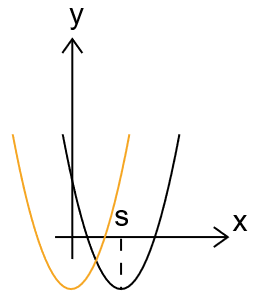
Berechnen Sie den Punkt $x=s$, an dem die Parabel ihr Minimum annimt.
Verschieben Sie anschließend die Parabel um diesen Wert nach links (orange Parabel).
Finden Sie die Nullstellen der verschobenen Funktion, und verschieben Sie diese wieder zurück, um auf die $p$-$q$ Formel der ursprünglichen Funktion zu kommen.

Lösung#

\[\begin{split}\begin{align} \frac{df}{dx}&=2x+p=0\\ s &= -\frac{p}{2} \end{align}\end{split}\]

Verschiebung um $s$:

\[\begin{split}\begin{align} (x-\frac{p}{2})^2+p(x-\frac{p}{2})+q&=0\\ x^2-px+\left(\frac{p}{2}\right)^2+px-\frac{p^2}{2}+q&=0\\ x^2-\frac{p^2}{4}+q&=0\\ x^2&=\frac{p^2}{4}-q\\ x&=\pm\sqrt{\frac{p^2}{4}-q} \end{align}\end{split}\]

Verschiebung wieder Rückgängig machen:

\[\begin{split}\begin{align} x + \frac{p}{2}&=\pm\sqrt{\frac{p^2}{4}-q}\\ x&=-\frac{p}{2}\pm\sqrt{\frac{p^2}{4}-q} \end{align}\end{split}\]

Aufgabe 19: Differenzieren#

Berechnen Sie die jeweils die erste Ableitung für Folgende Funktionen:

$x^2 e^x$
$\cos(x)e^{-x}$
$\ln(\ln(x)$
$\frac{\sqrt{x} \sin(x)}{\ln(x)}$

Lösung#

$(2x + x^2)e^x$
$-\sin(x)e^{-x} - \cos(x)e^{-x}$
$\dfrac{1}{x \ln(x)}$
$\dfrac{(2x \cos(x) + \sin(x)) \ln(x) - 2 \sin(x)}{2\sqrt{x}(\ln(x))^2}$

Aufgabe 20: Extremwerte#

Die Summe von zwei positiven Zahlen $x$ und $y$ ist 12. Was ist der kleinstmögliche Wert für die Summe ihrer Quadrate $x^2 + y^2$? Begründen Sie Ihre Antwort mit einer passenden Rechnung.
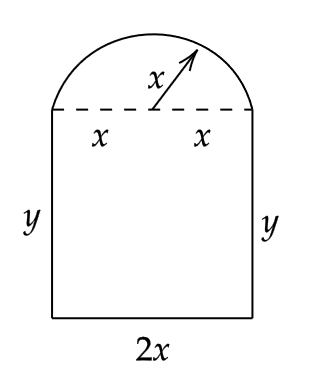
Der Querschnitt eines Tunnels besteht aus einem Rechteck mit aufgesetztem Halbkreis, siehe Abbildung. Wie müssen die Abmessungen $(x, y)$ gewählt werden, damit bei vorgegebenem Umfang $U$ des Tunnelquerschnitts die Querschnittsfläche des Tunnels möglichst groß wird?

Lösung#

Rechnung: $$\begin{align} x + y &= 12 \implies x = 12 - y \\ f(x,y) &= x^2 + y^2 \\ f(y) &= (12 - y)^2 + y^2 = 2y^2 - 24y + 144 \\ \frac{\text{d} f(y)}{\text{d} y} &= 4y - 24 = 0 \implies y = 6 \implies x = 6 \end{align}$$
Rechnung: $$\begin{align} A &= 2xy + \frac{1}{2}\pi x^2 \\ U &= 2x + 2y + \pi x \implies y = \frac{U - 2x - \pi x}{2} \\ A(x) &= xU - 2x^2 - \frac{\pi x^2}{2} \\ \frac{\text{d} A(x)}{\text{d} x} &= U - 4x - \pi x = 0 \implies x = \frac{U}{4 + \pi} \\ \text{Einsetzen in } U &= 2x + 2y + \pi x \implies y = \frac{U}{4 + \pi} \end{align}$$

Aufgabe 21: Unendliche Taylorreihe#

Bestimmen Sie die unendliche Taylorreihe $$\sum_{k = 0}^{\infty}\frac{f(x_o)^{(k)}}{k !}(x - x_0)^k$$ der Funktion $f(x) = \cos(x)$ an der Stelle $x_0 = 0$.

Hinweis: Berechnen Sie die Ableitungen der Funktion an der Stelle $x_0$ wie in der Formel beschrieben bis z. B. k = 5, hier sollten Sie dann eine Regelmäßigkeit erkennen, d. h. bestimmte Ergebnisse wiederholen sich. Schreiben Sie ausgehend von diesen Ergebnissen die gesamte Taylorreihe (d. h. bis ins Unendliche) in einer Summenformel auf. Das alternieren zwischen -1 und 1 kann durch $(-1)^k$ dargestellt werden und gerade Zahlen können Sie mit $2k$ beschreiben. Hilfreich könnte auch die folgende Seite sein.
Schreiben Sie eine Funktion in Python, die für einen Vektor von $x$-Werten die ersten $n + 1$ Summanden der Taylorreihe berechnet.
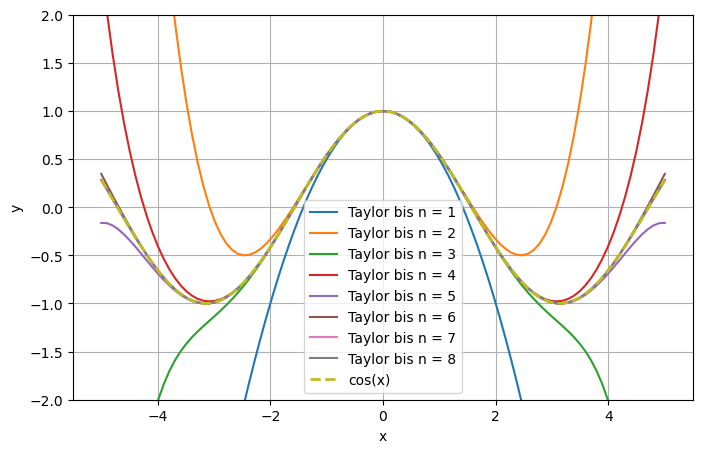
Plotten Sie die resultierende Funktion in Python zusammen mit der Funktion $\cos(x)$ für $x \in [-4, 4]$, beginnend mit $n = 1$ bis $n = 8$.

Lösung#

$\cos(x) = \sum_{k=0}^{\infty} (-1)^k \frac{x^{2k}}{2k!}$

# 2.

def T(x, n):
    T = 1
    for k in range(1, n + 1):
        T = T + (-1)**k*(x**(2*k))/(math.factorial(2*k))
    return T

# 3.

x = np.linspace(-5, 5, 100)
n_list = list(range(1, 8 + 1))

plt.figure(figsize=(8, 5))
for n in n_list:
    plt.plot(x, T(x, n), label=f"Taylor bis n = {n}")
plt.plot(x, np.cos(x), '--', linewidth=2, label="cos(x)")
plt.ylim(-2, 2)
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.grid(True)

Angewandte Mathematik

Lösungen

Contents

Lösungen#

Python-Pakete#

Aufgabe 1: Ableiten#

Lösung#

Aufgabe 2: Differenzieren, Tangente#

Lösung#

Aufgabe 3: Tangentengleichung#

Lösung#

Aufgabe 4: Differenzieren, Extrema#

Lösung#

Aufgabe 5: Kurvendiskussion#

Lösung#

Aufgabe 6: Extremwerte#

Lösung#

Aufgabe 7: maximale Bremskraft#

Lösung#

Aufgabe 8: kleinster Abstand von Massenpunkten#

Lösung#

Aufgabe 9: periodische Extremwerte#

Lösung#

Aufgabe 10: Taylor-Reihen#

Lösung#

Aufgabe 11: Taylor-Reihe des Kehrwerts#

Lösung#

Aufgabe 12: Taylor-Reihe einer Wurzelfunktion#

Lösung#

Aufgabe 13: Taylorreihe des Gravitationalspotentials#

Lösung#

Aufgabe 14: Differentialquotient und Ableitungsregeln#

Lösung#

Aufgabe 15: Differenzenquotient#

Lösung#

Aufgabe 16: Minimaler Abfall#

Lösung#

Aufgabe 17: Rinne mit maximalem Fassungsvermögen#

Lösung#

Aufgabe 18: Quadratische Gleichung via Differentialrechnung und Verschiebungen#

Lösung#

Aufgabe 19: Differenzieren#

Lösung#

Aufgabe 20: Extremwerte#

Lösung#

Aufgabe 21: Unendliche Taylorreihe#

Lösung#