Vorlesung
Contents
Vorlesung#
Konfiguration und Python-Pakete#
import numpy as np
import matplotlib.pyplot as plt
Einführung#
Differentiale Größen#
Oft ist nicht (nur) der Wert einer Größe \(y\) in Abhängigkeit einer anderen Größe \(x\) interessant sondern die Änderung der Größe \(y\) im Verhältnis zur Änderung der anderen Größe \(x\). Man arbeitet dann mit Begriffen wie (Änderungs-)Rate, Preis, Fluss, Geschwindigkeit, Trend, Steigung, spezifische Größe, (z. B. Wärme-)Kapazität, Ableitung, partielle Ableitung, totale Ableitung, Differential, Gradient, etc..
Mathematisch wird die Abhängigkeit einer Größe \(y\) von einer Größe \(x\) als Funktion \(y = f(x)\), oder kurz \(y(x)\), beschrieben. Hängt \(y\) von \(n\) anderen Größen \(x_1, x_2, \ldots , x_n\) ab, dann betrachtet man eine Funktion \(y = f(x_1, x_2, \ldots , x_n),\) oder kurz \(y(x_1, x_2, \ldots , x_n)\). Die Berechnung und Verwendung der Änderung von \(y\) pro Änderung von \(x\) bzw. \(x_k\) ist das Gebiet der eindimensionalen bzw. mehrdimensionalen Differentialrechnung.
Auswahl an Anwendungen der Differentialrechnung#
lineare Approximation von Funktionen
Taylorreihe: polynomiale Approximation von Funktionen
Optimalitätsbedingungen für nicht-lineare Optimierung
Lösen nicht-linearer Gleichungen und Gleichungssysteme
kontinuierliche, dynamische Systeme: gewöhnliche und partielle Differentialgleichungen
Physik, Chemie, Technik: Mechanik, Thermodynamik, Elektrodynamik etc.
Variationsrechnung, Theorie der optimalen Steuerungen
Lineare Approximation#
Wir approximieren die Änderung einer Funktion bei einem bestimmten Inputwert bzw. Arbeitspunkt in linearer Weise. Die (lineare) Approximation einer Funktion selbst folgt später, siehe Tangente und Taylorreihe.
Wir behandeln in diesem Abschnitt den eindimensionalen Fall einer Funktion \(y = f(x)\) und dies zuerst an folgendem
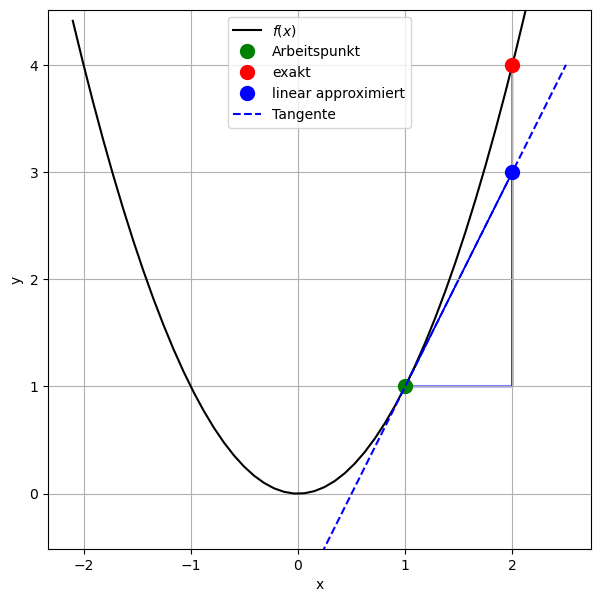
Beispiel: \(y = f(x) = x^2\), lineare Approximation bei \(x_0 = 1\), Inputänderung \(\Delta x = 1\)
# Funktion f(x):
def f(x):
return x**2
# erste Ableitung f'(x):
def f_p(x):
return 2*x
# Vektor von x-Werten zum Plotten:
x = np.linspace(-2.1, 2.5)
# Stelle der Approximation:
x0 = 1
y0 = f(x0)
# Änderungen:
delta_x = 1 # frei gewählte Änderung der unabhängigen Größe x
dx = delta_x # Die lineare Approximation dx von delta_x ist gleich delta_x,
# da x eine unabhängige Größe ist.
print(f"delta_x = {delta_x}")
print(f"dx = {dx}")
delta_y = f(x0 + dx) - f(x0) # wahre/exakte Änderung, nicht linear approximiert
dy = f_p(x0)*dx # lineare Approximation von delta_y
print(f"delta_y = {delta_y}")
print(f"dy = {dy}")
# Graph:
plt.figure(figsize=(7, 7))
plt.plot(x, f(x), color='black', label="$f(x)$")
plt.plot(x0, y0, 'o', color='green',
markersize=10, label="Arbeitspunkt")
plt.plot(x0 + dx, y0 + delta_y, 'o', color='red',
markersize=10, label="exakt")
plt.plot(x0 + dx, y0 + dy, 'o', color='blue',
markersize=10, label="linear approximiert")
plt.plot(x, y0 + f_p(x0)*(x - x0), '--b', label='Tangente')
plt.arrow(x0, y0, dx, 0, color='blue')
plt.arrow(x0 + dx, y0, 0, delta_y, color='red')
plt.arrow(x0 + dx, y0, 0, dy, color='blue')
plt.arrow(x0 , y0, dx, dy, color='blue')
plt.axis('equal')
plt.ylim(-.5, 4.5)
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='upper center')
plt.grid(True)
delta_x = 1
dx = 1
delta_y = 3
dy = 2
Nomenklatur#
\(x_0\) ist die Stelle (Argument, Input), an der die Änderung der Funktion linear approximiert wird.
\(\Delta x\) ist die frei gewählte Differenz (Änderung) der unabhängigen Inputgröße (Variablen) \(x\) bei \(x_0\).
\(\text{d}x\) ist die lineare Approximation von \(\Delta x\). Da \(x\) keine Funktion einer anderen Größe ist, d. h. \(x\) ist eine unabhängige Variable, ist die Approximation fehlerfei und man erhält \(\text{d}x = \Delta x\). Wir schreiben vorwiegend \(\text{d}x\).
\(\Delta y\) ist die exakte (wahre) Differenz (Änderung) der Outputgröße \(y\) bei Änderung der Inputgröße um \(\Delta x\) bei \(x_0\).
\(\text{d}y\) ist die lineare Approximation von \(\Delta y\).
Erste Ableitung#
Berechnungen:
\(\Delta y = f(x_0 + \Delta x) - f(x_0)\)
\(\text{d}y = f'(x_0)\,\text{d}x\). Daraus folgt \(\frac{\text{d}y}{\text{d}x} = f'(x_0)\).
\(\Delta y\) hängt im allgemeinen nicht-linear von \(\Delta x\) ab. Die lineare Approximation \(\text{d}y\) dieser Abhängigkeit ist für eindimensionale Funktionen von der Form \(\text{d}y = k\,\text{d}x\) für eine bestimmte Zahl \(k\). Diese Zahl \(k\) ist die erste Ableitung \(f'(x_0)\) der Funktion \(f\) bei \(x_0\).
Bemerkungen:
Für nicht-lineare Funktionen gilt im Allgemeinen \(\Delta y \neq \text{d}y\).
Für lineare Funktionen gilt immer \(\Delta y = \text{d}y\).
Je kleiner \(\text{d}x\) umso besser approximiert \(\text{d}y\) den wahren Wert \(\Delta y\).
Die erste Ableitung \(f'(x_0)\) der Funktion \(f\) bei \(x_0\) gibt die Änderungsrate von \(f\) bei \(x_0\) pro \(x\)-Einheit an und entspricht der Steigung der Tangente an den Graphen von \(f\) bei \(x_0\). Wird die Stelle \(x_0\) nicht spezifiziert, so erhält man eine Funktion von \(x\) und schreibt \(f'(x)\) oder kurz \(f'\). Oft wird auch \(y'(x_0)\), \(y'(x)\), \(y'\), \(\dot{y}(x_0)\), \(\dot{y}(x)\), oder \(\dot{y}\) sowie \(\frac{\text{d}y}{\text{d}x}\), \(\frac{\text{d}f}{\text{d}x}\) etc. verwendet.
Differenzenquotient: Die erste Ableitung (Steigung der Tangente) \(f'(x_0) = \frac{\text{d}y}{\text{d}x}\) ist der Grenzwert des Differenzenquotienten (Steigung der Sekante) \(\frac{\Delta y}{\Delta x}\) für \(\Delta x \to 0\).
Ableitung elementarer Funktionen#
\(f(x)\) |
\(f'(x)\) |
|---|---|
\(x^n\) |
\(nx^{n-1}\) |
\(e^x\) |
\(e^x\) |
\(\ln(x)\) |
\(\frac{1}{x}\) |
\(\sin(x)\) |
\(\cos(x)\) |
\(\cos(x)\) |
\(-\sin(x)\) |
Mehr finden Sie in der Literatur und im Internet.
Ableitungsregeln#
Faktorregel: Für jede Konstante \(c\) gilt
Beispiel: \((3x^2)' = 3(x^2)' = 3\cdot 2x = 6x\)
Summenregel:
Beispiel: \([\sin(x) + e^x]' = [\sin(x)]' + (e^x)' = \cos(x) + e^x\)
Produktregel:
Beispiel: \([\sin(x) \cdot e^x]' = \cos(x) \cdot e^x + \sin(x) \cdot e^x\)
Quotientenregel:
Beispiel: \(\frac{\sin(x)}{e^x} = \frac{\cos(x) \cdot e^x - \sin(x) \cdot e^x}{e^{2x}} = \frac{\cos(x) - \sin(x)}{e^{x}}\)
Kettenregel:
Beispiel: \([\sin(3x^2 + 4x)]'=\cos(3x^2 + 4x) \cdot (6x + 4)\)
Extremwerte#
Notwendige Bedingung: Eine Funktion \(f(x)\), die an einer Stelle \(x_0\) ein lokales Optimum (lokales Minimum oder lokales Maximum, allgemein einen Extremwert) hat, muss das Optimalitätskriterium \(f'(x_0) = 0\) erfüllen.
Hinreichende Bedingung: Umgekehrt gilt:
Wenn \(f'(x_0) = 0\) und \(f''(x_0) > 0\), dann hat \(f\) bei \(x_0\) ein lokales Minimum.
Wenn \(f'(x_0) = 0\) und \(f''(x_0) < 0\), dann hat \(f\) bei \(x_0\) ein lokales Maximum.
Allgemeinere hinreichende Bedingungen finden Sie in der Literatur, z. B. im Buch “Mathematik kompakt”, 2013 von Stry und Schwenkert auf Seite 236.
Taylorreihe#
Wir betrachten eine Funktion \(f(x)\) mit einer Inputvariablen \(x\). Der Funktionswert kann in der Umgebung einer frei gewählten Inputstelle \(x_0\) mittels der sogenannten Taylorreihe(nentwicklung) durch ein Polynom \(k\)-ter Ordnung approximiert werden, sodass der Funktionswert und alle Ableitungen bis inkl. \(k\)-ter Ordnung bei \(x_0\) übereinstimmen.
Beispiel: Taylorreihe dritter Ordnung, d. h. Polynom dritter Ordnung:
\[f(x) = f(x_0) + f'(x_0)(x - x_0) + \frac{1}{2}f''(x_0)(x - x_0)^2 + \frac{1}{6}f'''(x_0)(x - x_0)^3 + \text{Fehler}\]Die Taylorreihe 1. Ordnung entspricht der Tangente an den Graphen von \(f\) bei \(x_0\): \(f_{\text{Tang.}}(x) = f(x_0) + f'(x_0)(x - x_0)\)
Die Taylorreihe 2. Ordnung entspricht der Schmiegeparabel an den Graphen von \(f\) bei \(x_0\): \(f_{\text{Parab.}}(x) = f(x_0) + f'(x_0)(x - x_0) + \frac{1}{2}f''(x_0)(x - x_0)^2\)
unendliche Taylorreihe:
\[f(x) = \sum_{k=0}^\infty \frac{1}{k!}f^{(k)}(x_0)(x - x_0)^k.\]Dabei bezeichnet \(f^{(k)}\) die \(k\)-te Ableitung von \(f\).
Beispiele:
Exponentialfunktion bei \(x_0 = 0\): \(e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + \ldots = \sum_{k=0}^\infty \frac{x^k}{k!}\)
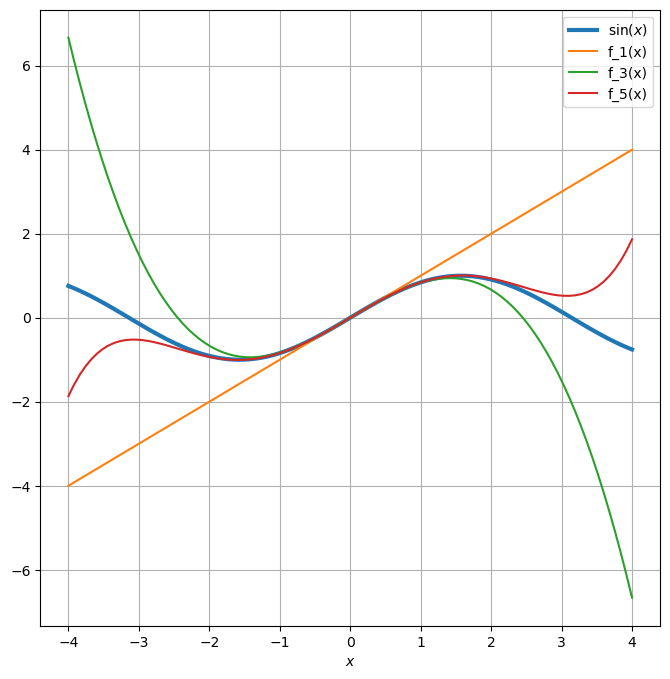
Sinus bei \(x_0 = 0\): \(\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \ldots\), siehe Code unten
Cosinus bei \(x_0 = 0\): \(\cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \ldots\)
vgl. \(e^{i\varphi} = \cos(\varphi) + i\sin(\varphi)\)
siehe Wikipedia
# Taylorreihe der Sinusfunktion bei x_0 = 0:
x = np.linspace(-4, 4, num=100)
f_1 = lambda x: x
f_3 = lambda x: x - 1/(3*2*1)*x**3
f_5 = lambda x: x - 1/(3*2*1)*x**3 + 1/(5*4*3*2*1)*x**5
plt.figure(figsize=(8,8))
plt.plot(x, np.sin(x), linewidth=3, label="$\sin(x)$")
plt.plot(x, f_1(x), label="f_1(x)")
plt.plot(x, f_3(x), label="f_3(x)")
plt.plot(x, f_5(x), label="f_5(x)")
plt.xlabel("$x$")
plt.legend()
plt.grid(True)