Schriftlicher Teil

Aufgabe 1 (3 + 1 = 4 Punkte)

1. Welche der folgenden Funktionen sind gerade, ungerade oder weder noch? Begründen Sie Ihre Antwort mit einer Rechnung, die mit \(f(-x) = \) beginnt.

   1. \(f(x) = \frac{x^2}{x^3 + x}\)

   2. \(f(x) = \cos(2x) - \cos(x)\)

   3. \(f(x) = \ln(|x|)\)

2. Wie ändert sich die Funktionsgleichung \(f(x) = e^{2x + 1}\), wenn deren Graph um zwei Einheiten in die negative \(x\)-Richtung und um eine Einheit in die positive \(y\)-Richtung verschoben wird?

Lösung

1. Gerade, ungerade oder weder noch?

   1. ungerade

   2. gerade

   3. gerade

2. \(f(x) = e^{2(x + 2) + 1} + 1 = e^{2x + 5} + 1\)

Aufgabe 2 (1 + 1 + 1 = 3 Punkte)

Wir betrachten die Funktion

\[f(x) = \frac{e^{-x} - 2}{x + 1}.\]

Bestimmen Sie von der Funktion:

1. die größtmögliche Definitionsmenge

2. alle Nullstellen

3. alle Pole

Lösung

1. \(\mathbb{R} \setminus \{-1\}\)

2. \(x = -\ln(2)\)

3. \(x = -1\)

Aufgabe 3 (5 Punkte)

Bestimmen Sie die Extremwerte der Funktion \(f(x) = x^3 e^{-2x}\). Handelt es sich jeweils um ein lokales Maximum, ein lokales Minimum oder einen Sattelpunkt?

Lösung

Lokales Maximum bei \(x=1.5\), Sattelpunkt bei \(x=0\), Quelle: Papula, Lothar (2018): Mathematik für Ingenieure und Naturwissenschaftler - Klausur- und Übungsaufgaben. 5. Auflage, Springer Vieweg: Aufgabe B76, Seite 109 f.

Aufgabe 4 (3 + 2 = 5 Punkte)

1. Berechnen Sie die Taylor-Reihe bis zur dritten Ordnung von \(\sin(x)\) bei \(x_0 = 0\).

2. Gegeben ist die Formel \(A(x, y) = \frac{1}{2} x^2 \left( y - \sin(y) \right)\). Die Größen \(x\) und \(y\) wurden wie folgt gemessen: \(x = 10 \pm 0.5\), \(y = 1 \pm 0.1\). Wie lautet das Messergebnis für die indirekte Messgröße \(A\)?

Lösung

1. \(x - \frac{x^3}{6}\)

2. \(7.93 \pm 3.09\), Quelle: Papula, Lothar (2018): Mathematik für Ingenieure und Naturwissenschaftler - Klausur- und Übungsaufgaben. 5. Auflage, Springer Vieweg: Aufgabe E57, Seite 273 f.

import numpy as np

x  = 10.0
dx =  0.5
y  =  1.0
dy =  0.1

A = 0.5*x**2 * (y - np.sin(y)) 
dA_max = np.abs(x*(y - np.sin(y))*dx) + \
         np.abs(0.5*x**2 * (1 - np.cos(y))*dy)

print(f"{A:.2f} +/- {dA_max:.2f}")

7.93 +/- 3.09

Aufgabe 5 (4 Punkte)

Minimieren Sie die \(f(x,y) = 1 + x^2 + y^2 - 2x\) unter der Nebenbedingung \(2x + 3y = 6\).

Lösung

\(x = \frac{21}{13}\), \(y = \frac{12}{13}\)

Aufgabe 6 (2 + 2 = 4 Punkte)

1. Warum ist backtracking beim Gradientenverfahren zur numerischen Lösung nichtlinearer Optimierungsprobleme hilfreich?

2. Erklären Sie das Newton-Verfahren zur numerischen Lösung nichtlinearer Gleichungen in Worten und ohne Formeln, und begründen Sie, warum es funktioniert.

Lösung

1. Zur Schrittweitenregulierung, damit an der neuen Stelle der Funktionswert nicht größer als der alte ist.

2. Approximation der Funktion mit der Tangente an der aktuellen Stelle, Nullstelle der Tangente als Approximation der Nullstelle der Funktion liefert neue Stelle.

Aufgabe 7 (4 Punkte)

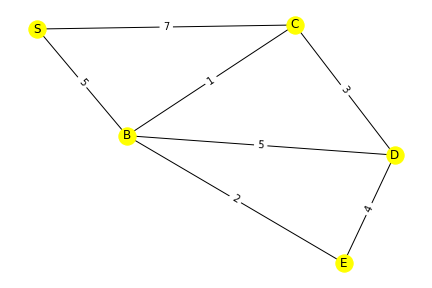
Bestimmen Sie vom Startknoten S aus die kürzesten Wege und deren Distanzen zu allen anderen Knoten, indem Sie die Tabelle unten weiterführen.

S	B	C	D	E
0	ue.	ue.	ue.	ue.

Dabei steht ue. für unendlich.

Lösung

S	B	C	D	E
0	ue.	ue.	ue.	ue.
-	5\(_S\)	7\(_S\)	ue.	ue.
-	-	6\(_B\)	10\(_B\)	7\(_B\)
-	-	-	9\(_C\)	7\(_B\)
-	-	-	9\(_C\)	-