Vorlesung

Konfiguration und Python-Pakete

import numpy as np
import matplotlib.pyplot as plt

Gradientenverfahren

Wir betrachten den Fall einer Minimierung ohne Nebenbedingungen und verwenden dafür ein einfaches Gradientenverfahren, nämlich das Verfahren des steilsten Abstiegs. Nachteil: oftmals sehr langsam.

Erster Versuch

Wir betrachten die Minimierung einer \(n\)-dimensionalen Funktion \(y = f(x) = f(x_1, x_2, \ldots, x_n)\). Das Argument \(x\) ist hier also ein \(n\)-dimensionaler Vektor, den wir als Punkt im \(\mathbb{R}^n\) interpretieren. Am Startpunkt \(x_0\) bestimmen wir den Gradienten

\[\begin{split}\nabla f(x_0) = \begin{pmatrix}\frac{\partial f}{\partial x_1}(x_0) \\ \frac{\partial f}{\partial x_2}(x_0) \\ \vdots \\ \frac{\partial f}{\partial x_n}(x_0) \end{pmatrix}.\end{split}\]

Der Gradient bei \(x_0\) zeigt in die Richtung der stärksten Zunahme von \(f\) bei \(x_0\). Der negative Gradient \(-\nabla f(x_0)\) zeigt somit in die Richtung der stärksten Abnahme von \(f\) bei \(x_0\). Da wir ein Minimum finden wollen, entschließen wir uns, vom Startpunkt den Schritt \(-\nabla f(x_0)\) in die Richtung des steilsten Abstiegs zu gehen und landen danach beim Punkt

\[x_1 = x_0 - \nabla f(x_0).\]

Diesen Vorgehensweise wiederholen wir solange, bis die Folge von Punkten \(x_0, x_1, x_2, \ldots\) sich nicht mehr (viel) ändert und daher \(\nabla f\) beim letzten Punkt \(x_N\) klein (genug) ist. Achtung: Aus \(\nabla f(p) = 0\) an einem Punkt \(p \in \mathbb{R}^n\) folgt nicht zwingend, dass \(p\) ein Minimum ist. Wir erhalten aus dem Verfahren also “nur” Kandidaten für Minima.

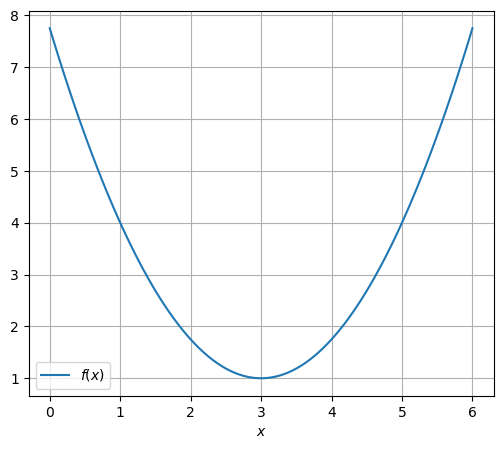
1-dim. Beispiele:

\[\begin{split}\begin{align} f(x) &= 0.75(x - 3)^2 + 1 \\ f'(x) &= 1.5(x - 3) \end{align}\end{split}\]

def f(x):
    return 0.75*(x - 3)**2 + 1

def grad_f(x):
    return 1.5*(x - 3)

x_plot = np.linspace(0, 6, num=100)

plt.figure(figsize=(6, 5))
plt.plot(x_plot, f(x_plot), label='$f(x)$')
plt.xlabel('$x$')
plt.legend()
plt.grid(True)

eps = 1e-3  # x-Genauigkeit und Genauigkeit für Gradienten
K   = 20    # maximale Anzahl an Iterationsschritten

x = [5.5]   # Startstelle am Beginn der Liste der besuchten Stellen

k = 0
while k < K:
    x_new = x[k] - grad_f(x[k])
    x.append(x_new)
    k += 1
    if np.abs(x[k] - x[k-1]) < eps:
        break
print(f"letzte Stelle x[{k}] = {x[k]:.16f}")

letzte Stelle x[13] = 2.9996948242187500

for k, x_k in enumerate(x):
    print(f"x[{k:2.0f}] ={x_k:20.16f}")

x[ 0] =  5.5000000000000000
x[ 1] =  1.7500000000000000
x[ 2] =  3.6250000000000000
x[ 3] =  2.6875000000000000
x[ 4] =  3.1562500000000000
x[ 5] =  2.9218750000000000
x[ 6] =  3.0390625000000000
x[ 7] =  2.9804687500000000
x[ 8] =  3.0097656250000000
x[ 9] =  2.9951171875000000
x[10] =  3.0024414062500000
x[11] =  2.9987792968750000
x[12] =  3.0006103515625000
x[13] =  2.9996948242187500

x_array = np.array(x)

plt.figure(figsize=(6, 5))
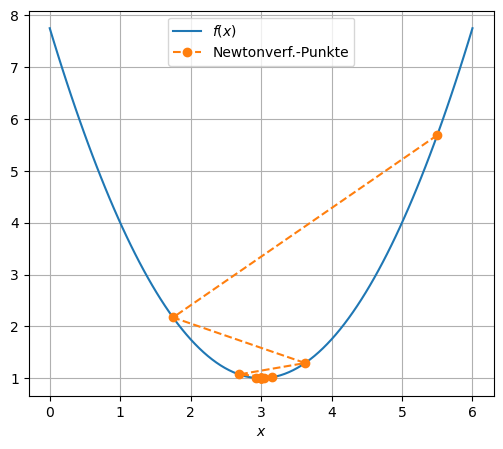
plt.plot(x_plot, f(x_plot), label='$f(x)$')
plt.plot(x_array, f(x_array), 'o--', label='Newtonverf.-Punkte')
plt.xlabel('$x$')
plt.legend()
plt.grid(True)

Um das Verfahren besser für verschiedene Funktionen und Startwerten vergleichen zu können, erstellen wir eine Python-Funktion:

def V(f, grad_f, x_0, eps=1e-3, K=20,
      print_x=True, plot_graph=True):
    """
    1-dim (zu) simples Verfahren zur Minimierung ohne
    Nebenbedingungen mittels Gradientenschritt
    """
    x = [x_0]    # Startstelle am Beginn der Liste der besuchten Stellen
    k = 0
    while k < K:
        x_new = x[k] - grad_f(x[k])
        x.append(x_new)
        k += 1
        if np.abs(x[k] - x[k-1]) < eps:
            break
    print(f"letzte Stelle x[{k}] = {x[k]:.16f}")

    if print_x:
        for k, x_k in enumerate(x):
            print(f"x[{k:2.0f}] ={x_k:20.16f}")

    if plot_graph:
        x_array = np.array(x)
        x_plot = np.linspace(np.min(x_array) - 1,
                             np.max(x_array) + 1)
        plt.figure(figsize=(6, 5))
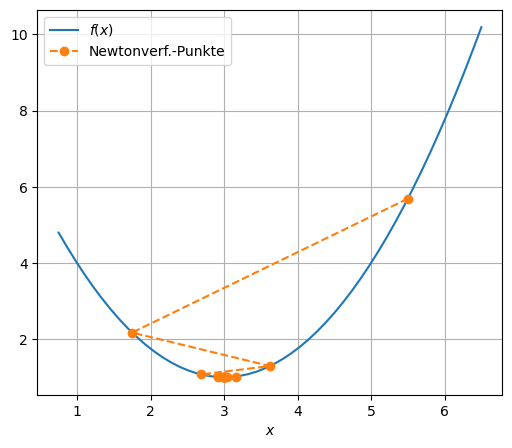
        plt.plot(x_plot, f(x_plot), label='$f(x)$')
        plt.plot(x_array, f(x_array), 'o--', label='Newtonverf.-Punkte')
        plt.xlabel('$x$')
        plt.legend()
        plt.grid(True)

f      = lambda x: 0.75*(x - 3)**2 + 1
grad_f = lambda x: 1.5*(x - 3)
x_0    = 5.5

V(f, grad_f, x_0)

letzte Stelle x[13] = 2.9996948242187500
x[ 0] =  5.5000000000000000
x[ 1] =  1.7500000000000000
x[ 2] =  3.6250000000000000
x[ 3] =  2.6875000000000000
x[ 4] =  3.1562500000000000
x[ 5] =  2.9218750000000000
x[ 6] =  3.0390625000000000
x[ 7] =  2.9804687500000000
x[ 8] =  3.0097656250000000
x[ 9] =  2.9951171875000000
x[10] =  3.0024414062500000
x[11] =  2.9987792968750000
x[12] =  3.0006103515625000
x[13] =  2.9996948242187500

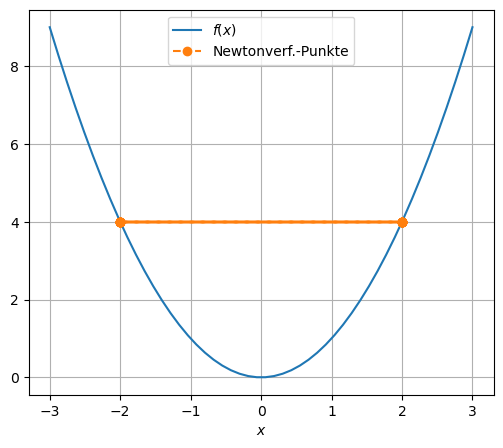
f      = lambda x: x**2
grad_f = lambda x: 2*x
x_0    = 2

V(f, grad_f, x_0)

letzte Stelle x[20] = 2.0000000000000000
x[ 0] =  2.0000000000000000
x[ 1] = -2.0000000000000000
x[ 2] =  2.0000000000000000
x[ 3] = -2.0000000000000000
x[ 4] =  2.0000000000000000
x[ 5] = -2.0000000000000000
x[ 6] =  2.0000000000000000
x[ 7] = -2.0000000000000000
x[ 8] =  2.0000000000000000
x[ 9] = -2.0000000000000000
x[10] =  2.0000000000000000
x[11] = -2.0000000000000000
x[12] =  2.0000000000000000
x[13] = -2.0000000000000000
x[14] =  2.0000000000000000
x[15] = -2.0000000000000000
x[16] =  2.0000000000000000
x[17] = -2.0000000000000000
x[18] =  2.0000000000000000
x[19] = -2.0000000000000000
x[20] =  2.0000000000000000

f      = lambda x: 1.5*x**2
grad_f = lambda x: 3*x
x_0    = 2

V(f, grad_f, x_0)

letzte Stelle x[20] = 2097152.0000000000000000
x[ 0] =  2.0000000000000000
x[ 1] = -4.0000000000000000
x[ 2] =  8.0000000000000000
x[ 3] =-16.0000000000000000
x[ 4] = 32.0000000000000000
x[ 5] =-64.0000000000000000
x[ 6] =128.0000000000000000
x[ 7] =-256.0000000000000000
x[ 8] =512.0000000000000000
x[ 9] =-1024.0000000000000000
x[10] =2048.0000000000000000
x[11] =-4096.0000000000000000
x[12] =8192.0000000000000000
x[13] =-16384.0000000000000000
x[14] =32768.0000000000000000
x[15] =-65536.0000000000000000
x[16] =131072.0000000000000000
x[17] =-262144.0000000000000000
x[18] =524288.0000000000000000
x[19] =-1048576.0000000000000000
x[20] =2097152.0000000000000000

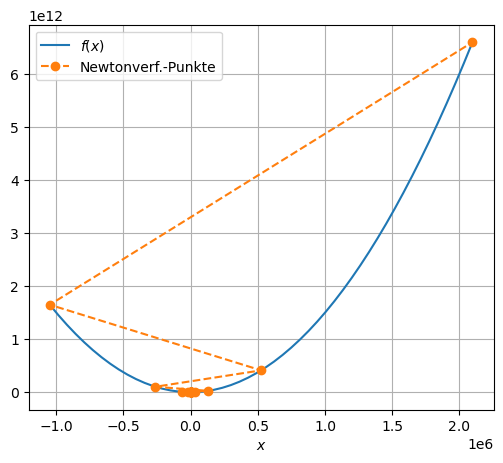
Die Schritte \(-\nabla f(x_k)\) sind in den letzten zwei Beispielen zu lange. Daher modifizieren wir unseren Algorithmus durch eine Anpassung der Schrittweite, d. h. der Länge des Schritts \(-\nabla f(x_k)\):

Backtracking

Beim Backtracking halbiert man den Schritt so lange, bis der Funktionswert der neuen Stelle kleiner ist als der alte.

def BT_1dim(f, grad_f, x_0, eps=1e-3, K=20,
            print_x=True, plot_graph=True):
    """
    1-dim. Gradientenschritt mit Backtracking
    """
    x = [x_0]  # Startstelle am Beginn der Liste der besuchten Stellen
    k = 0
    while k < K:
        t = 1
        x_new = x[k] - t*grad_f(x[k])
        while f(x_new) >= f(x[k]):
            t = t/2
            x_new = x[k] - t*grad_f(x[k])
        x.append(x_new)
        k += 1
        if np.abs(x[k] - x[k-1]) < eps or np.abs(grad_f(x[k])) < eps:
            break
    print(f"letzte Stelle x[{k}] = {x[k]:.16f}")

    if print_x:
        for k, x_k in enumerate(x):
            print(f"x[{k:2.0f}] ={x_k:20.16f}")

    if plot_graph:
        x_array = np.array(x)
        x_plot = np.linspace(np.min(x_array) - 1,
                             np.max(x_array) + 1)
        plt.figure(figsize=(6, 5))
        plt.plot(x_plot, f(x_plot), label='$f(x)$')
        plt.plot(x_array, f(x_array), 'o--', label='NV_mit_BT.-Punkte')
        plt.xlabel('$x$')
        plt.legend()
        plt.grid(True)

if 1:
    f      = lambda x: x**2
    grad_f = lambda x: 2*x
    x_0    = 2
else:
    f      = lambda x: 1.5*x**2
    grad_f = lambda x: 3*x
    x_0    = 2

BT_1dim(f, grad_f, x_0)

letzte Stelle x[1] = 0.0000000000000000
x[ 0] =  2.0000000000000000
x[ 1] =  0.0000000000000000

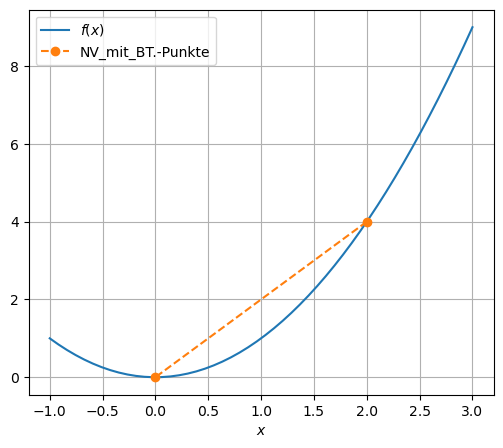
2-dim. Beispiel:

Wir suchen Minima der Funktion \(f(x,y) = e^{x + y} + e^{x - y} + e^{-x}\). Zuerst machen wir uns ein Bild, in diesem Fall einen Konturplot, der Funktion:

x = np.linspace(-3.0, 1.0, 200)
y = np.linspace(-2.5, 2.5, 200)
X, Y = np.meshgrid(x, y)
Z = np.exp(X + Y) + np.exp(X - Y) + np.exp(-X)

plt.figure(figsize=(7, 7))
cs = plt.contour(X, Y, Z, 30, cmap='coolwarm')
plt.clabel(cs, inline=1)
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)

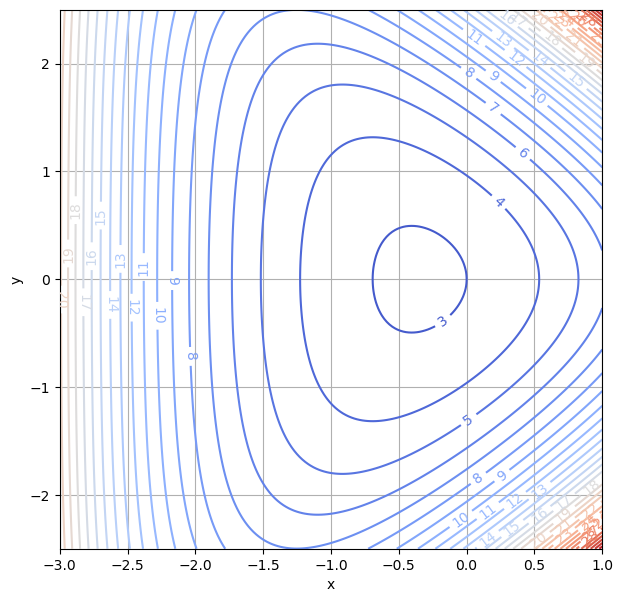
Der Gradient von \(f(x,y) = e^{x + y} + e^{x - y} + e^{-x}\) ist \(\nabla f(x, y) = \begin{pmatrix} e^{x + y} + e^{x - y} - e^{-x} \\ e^{x + y} - e^{x - y} \end{pmatrix}\).

Für die Implementierung schreiben wir \(p_k = (x_k,y_k)\) und verwenden 1-dim numpy-arrays.

def f(p_k):
    x = p_k[0]
    y = p_k[1]
    return np.exp(x + y) + np.exp(x - y) + np.exp(-x)

def grad_f(p_k):
    x = p_k[0]
    y = p_k[1]
    f_x = np.exp(x + y) + np.exp(x - y) - np.exp(-x)
    f_y = np.exp(x + y) - np.exp(x - y)
    return np.array([f_x, f_y])

def BT_ndim(f, grad_f, p_0, eps=1e-3, K=20):
    """
    n-dim. Gradientenschritt mit Backtracking
    """
    p = [p_0]   # Startstelle am Beginn der Liste der besuchten Stellen
    k = 0
    while k < K:
        t = 1
        p_new = p[k] - t*grad_f(p[k])
        while f(p_new) >= f(p[k]):
            t = t/2
            p_new = p[k] - t*grad_f(p[k])
        p.append(p_new)
        k += 1
        d = p[k] - p[k-1]
        abstand  = np.sqrt(np.sum([diff**2 for diff in d]))
        grad_abs = np.sqrt(np.sum([g**2 for g in grad_f(p[k])]))
        if abstand < eps or grad_abs < eps:
            break
    print(f"letzte Stelle p[{k}]  = {p[k]}")
    print(f"        mit f(p[{k}]) = {f(p[k])}")
    return p

p_0 = np.array([-2.0, 2.0])
p = BT_ndim(f, grad_f, p_0)

letzte Stelle p[12]  = [-3.46756442e-01  2.47315177e-06]
        mit f(p[12]) = 2.82842717203429

p_array = np.array(p)

plt.figure(figsize=(7, 7))
cs = plt.contour(X, Y, Z, 30, cmap='coolwarm')
plt.plot(p_array[:, 0], p_array[:, 1], 'o--')
plt.clabel(cs, inline=1)
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)

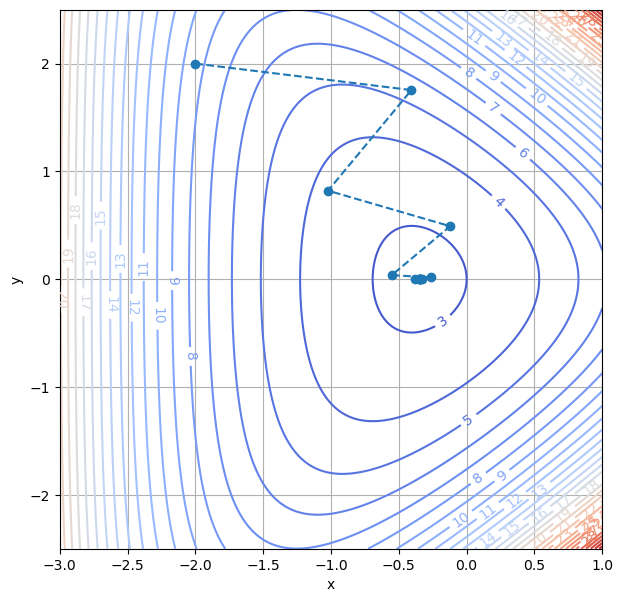
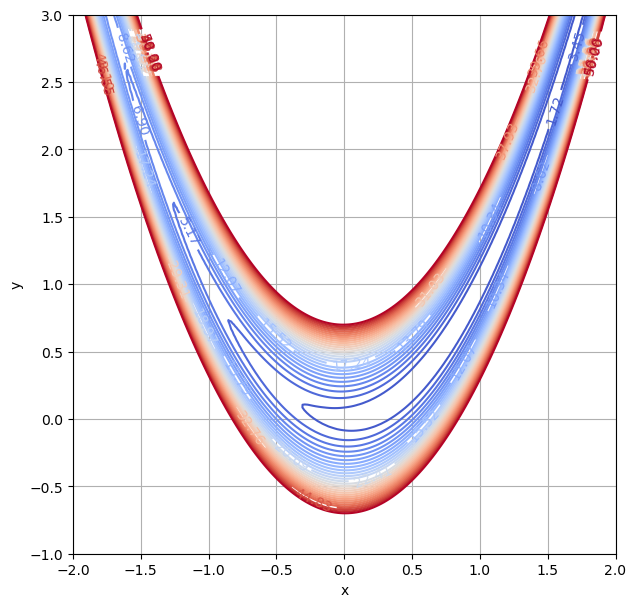
2-dim. Beispiel: Die Rosenbrock-Funktion \(f(x,y)=(a-x)^{2}+b(y-x^{2})^{2}\) hat ein Minimum bei \((a,a^{2})\) mit \(f(a,a^2)=0\).

a = 1
b = 100

x = np.linspace(-2.0, 2.0, 200)
y = np.linspace(-1.0, 3.0, 200)
X, Y = np.meshgrid(x, y)
Z = (a - X)**2 + b*(Y - X**2)**2

plt.figure(figsize=(7, 7))
levels = np.linspace(0, 50, num=30)
cs = plt.contour(X, Y, Z, levels, cmap='coolwarm')
plt.clabel(cs, inline=1)
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)

Der Gradient von \(f(x,y)=(a-x)^{2}+b(y-x^{2})^{2}\) ist \(\nabla f(x, y) = \begin{pmatrix} -2(a - x) - 4xb(y - x^2) \\ 2b(y - x^2) \end{pmatrix}\).

def f(p_k):
    x = p_k[0]
    y = p_k[1]
    return (a - x)**2 + b*(y - x**2)**2

def grad_f(p_k):
    x = p_k[0]
    y = p_k[1]
    f_x = -2*(a - x) - 4*x*b*(y - x**2)
    f_y = 2*b*(y - x**2)
    return np.array([f_x, f_y])

p_0 = np.array([-1.5, 1.95])
p = BT_ndim(f, grad_f, p_0)

letzte Stelle p[9]  = [1.71515212 2.94477353]
        mit f(p[9]) = 0.5123586641999825

p_array = np.array(p)
plt.figure(figsize=(7, 7))
levels = np.linspace(0, 50, num=30)
cs = plt.contour(X, Y, Z, levels, cmap='coolwarm')
plt.plot(p_array[:, 0], p_array[:, 1], 'o--')
plt.clabel(cs, inline=1)
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)

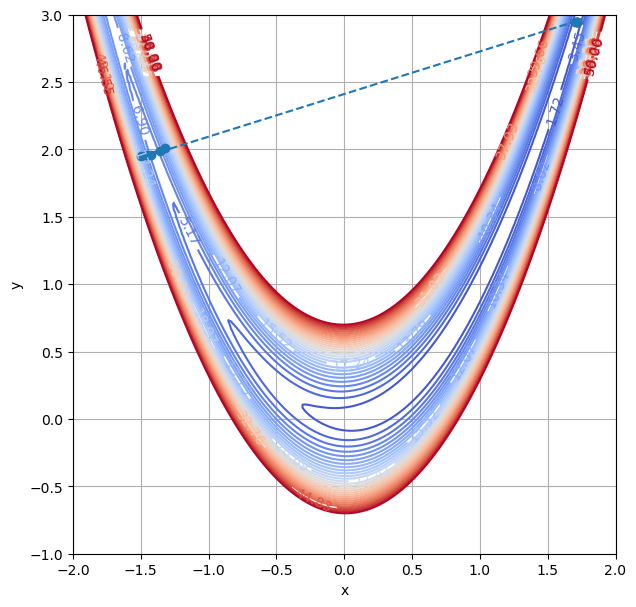
Unseren Algorithmus konvergiert nicht zum Minimum. Ausgeklügeltere Algorithmen schaffen das. Es wird auf folgende sehr kleine Auswahl an weiterführender Literatur verwiesen:

• Nocedal, Jorge; Wright, S. (2006): Numerical Optimization. 2. Aufl., Springer-Verlag.

• Vandenberghe, Lieven: lecture notes to the course Applied Numerical Computing at University of California, Los Angeles