Lösungen
Contents
Lösungen#
Konfiguration und Python-Pakete#
import numpy as np
import scipy.linalg as la # or: from scipy import linalg as la
import scipy.optimize as op
import matplotlib.pyplot as plt
Aufgabe 1: Partielle Ableitungen, ideales Gas, ÖPNV#
Ideales Gas: Das Volumen \(V\) einer bestimmten Menge eines idealen Gases ist durch die Temperatur \(T\) und den Druck \(p\) über die Formel \(V = 0.08\frac{T}{p}\) gegeben. Berechnen und interpretieren Sie \(\frac{\partial V}{\partial p}\) und \(\frac{\partial V}{\partial T}\) bei \(p = 20\) und \(T = 300\).
Öffentlicher Personennahverkehr: In einer Vorstadt haben Pendler die Möglichkeit mit dem Bus oder mit dem Zug in das Stadtzentrum zu kommen. Die Nachfrage nach diesen Verkehrsarten variiert mit ihrer Kosten. Sei \(B(b, z)\) die Anzahl der Menschen, die mit dem Bus fahren wird, wenn \(b\) der Preis für den Bus und \(z\) der Preis der Zug sind. Zum Beispiel: Bei \(B(4, 6) = 7000\) nehmen 7000 Pendler den Bus, wenn der Preis den Bus \(4\) ist und der Preis für den Zug \(6\) ist. Erklären Sie, warum \(\frac{\partial B}{\partial b} <0\) und \(\frac{\partial B}{\partial z}> 0\) gelten.
Lösung#
\(\frac{\partial V}{\partial p}(p,T) = -0.08\frac{T}{p^2}\) und \(\frac{\partial V}{\partial T}(p,T) = 0.08\frac{1}{p}\). Daher ist \(\frac{\partial V}{\partial p}(20, 300) = -0{,}06\) (Volumen wird kleiner bei steigendem Druck und gleichbleibender Temperatur) und \(\frac{\partial V}{\partial T}(20, 300) = 0{,}004\) (Volumen wird größer bei steigender Temperatur und gleichbleibendem Druck)
\(\frac{\partial B}{\partial b} <0\) weil steigende Buspreise bei gleichbleibenden Zugpreisen zu weiniger Verwendern der Busse führen, und \(\frac{\partial B}{\partial z}> 0\) weil umgekehrt steigende Zugpreise bei gleichbleibenden Buspreisen zu mehr Verwendern der Busse führen.
Aufgabe 2: Wärmeleitungsgleichung#
Zeigen Sie, dass die Temperaturfunktion
die Wärmeleitungsgleichung
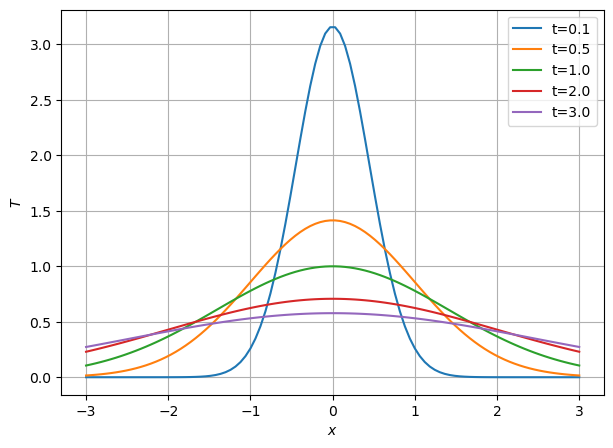
erfüllt. Plotten Sie die örtliche Temperaturverteilung für einige verschiedene Zeiten. Interpretieren Sie die Wärmeleitungsgleichung und die spezielle Lösung \(T(x,t)\).
Lösung#
\(\frac{\partial T}{\partial t}(x,t)\) berechnet sich mittels Produkt- und Kettenregel zu \(e^{-\frac{x^2}{4t}}\left( -\frac{1}{2\sqrt{t^3}} + \frac{x^2}{4\sqrt{t^5}} \right)\). \(\frac{\partial T}{\partial x}(x,t)\) berechnet sich mittels Kettenregel zu \(-\frac{1}{2\sqrt{t^3}}xe^{-\frac{x^2}{4t}}\) und daraus berechnet sich \(\frac{\partial^2 T}{\partial x^2}(x,t)\) mittels Produkt- und Kettenregel zu \(e^{-\frac{x^2}{4t}}\left( -\frac{1}{2\sqrt{t^3}} + \frac{x^2}{4\sqrt{t^5}} \right)\). Der Vergleich zeigt. dass \(\frac{\partial T}{\partial t}(x,t)= \frac{\partial^2 T}{\partial x^2}(x,t)\) erfüllt ist.
Interpretationen:
Wärmeleitungsgleichung: Die zeitliche Änderung ist gleich der örtlichen Krümmung. Wenn bei \((x,t)\) die Temperatur höher ist als in der örtlichen Umgebung, dann sinkt sie anschließend. Umgekehrt, wenn bei \((x,t)\) die Temperatur niedriger ist als in der örtlichen Umgebung, dann steigt sie anschließend.
Lösung \(T(x,t)\): Gaußglocke, die bei \(x=0\) zentriert ist und mit der Zeit “schmilzt”, d. h. breiter und niedriger wird.
x = np.linspace(-3, 3, num=100)
times = np.array([0.1, 0.5, 1, 2, 3])
plt.figure(figsize=(7, 5))
for t in times:
T = 1/np.sqrt(t)*np.exp(-x**2/(4*t))
plt.plot(x, T, label=f"{t=}")
plt.legend()
plt.xlabel("$x$")
plt.ylabel("$T$")
plt.grid(True)
Aufgabe 3: lineare Approximation und Funktionswertdifferenz#
Berechnen Sie das Differential der Funktion \(f:\mathbb{R}^2 \rightarrow\mathbb{R}: z(x, y) = e^{-(3x^2 + y^2)}\) allgemein und im Speziellen bei \((x_0, y_0)=(1,2)\). Wie groß ist der Unterschied zwischen der linearen Approximation \(\text{d}z\) der Funktionswertdifferenz und der wahren Funktionswertdifferenz \(\Delta z\) bei \((x_0, y_0)\), wenn \(\text{d}x = 0.1\) und \(\text{d}y = -0.2\)?
Lösung#
\(\text{d}z = \frac{\partial z}{\partial x}\text{d}x + \frac{\partial z}{\partial y} \text{d}y = e^{-(3x^2 + y^2)}(-6x) \text{d}x + e^{-(3x^2 + y^2)}(-2y) \text{d}y\), \(\Delta z (1,2) = e^{-(3(1.1)^2 + (1.8)^2)} - e^{-(3(1)^2 + (2)^2)}\), \(\text{d}z (1,2) = e^{-7}(-6) 0.1 + e^{-7}(-4) (-0.2)\). Siehe Code:
def z(x, y):
return np.exp(-(3*x**2 + y**2))
def dz(x_0, y_0, dx, dy):
return -np.exp(-(3*x_0**2 + y_0**2))*6*x_0*dx - np.exp(-(3*x_0**2 + y_0**2))*2*y_0*dy
x_0 = 1
y_0 = 2
dx = 0.1
dy = -0.2
print(f"wahre Differenz = {z(x_0 + dx, y_0 + dy) - z(x_0, y_0):.10f}")
print(f"linear approximierte Differenz = {dz(x_0, y_0, dx, dy):.10f}")
wahre Differenz = 0.0001265951
linear approximierte Differenz = 0.0001823764
Aufgabe 4: Wärmeverlust in einem Gebäude - Teil 1, partielle Ableitungen#
Ein rechteckiges Industriegebäude habe die Länge \(x\), die Breite \(y\) und die Höhe \(z\). In der Tabelle ist der Wärmeverlust pro Tag durch jede Seite des Gebäudes in geeigneten Energieeinheiten pro Quadratmeter Seitenfläche angegeben.
Dach |
Ostseite |
Westseite |
Nordseite |
Südseite |
Boden |
|---|---|---|---|---|---|
10 |
8 |
6 |
10 |
5 |
1 |
Der gesamte tägliche Wärmeverlust des Gebäudes sei mit Sei \(Q(x, y, z)\) bezeichnet.
Finden Sie eine Formel für \(Q(x, y, z)\).
Geben Sie den gesamten täglichen Wärmeverlust an, wenn das Gebäude 30 Meter lang, 12 Meter breit und 9 Meter hoch ist.
Berechnen und interpretieren Sie \(\frac{\partial Q}{\partial x} (30, 12, 9)\), \(\frac{\partial Q}{\partial y}(30, 12, 9)\) und \(\frac{\partial Q}{\partial z} (30, 12, 9)\).
Lösung#
\(Q(x,y,z) = 10xy + 8yz + 6yz + 10xz + 5xz + 1xy = 11xy + 14yz + 15xz\)
\(Q(30, 12, 9)\), siehe Code
Siehe Code
def Q(x,y,z):
return 11*x*y + 14*y*z + 15*x*z
def Q_x(x,y,z):
return 11*y + 15*z
def Q_y(x,y,z):
return 11*x + 14*z
def Q_z(x,y,z):
return 14*y + 15*x
x_0 = 30
y_0 = 12
z_0 = 9
print(f"gesamter täglicher Wärmeverlust = {Q(x_0, y_0, z_0):8.2f}")
print(f"Wärmeverlust pro Meter Längenänderung = {Q_x(x_0, y_0, z_0):8.2f}")
print(f"Wärmeverlust pro Meter Breitenänderung = {Q_y(x_0, y_0, z_0):8.2f}")
print(f"Wärmeverlust pro Meter Höhennänderung = {Q_z(x_0, y_0, z_0):8.2f}")
gesamter täglicher Wärmeverlust = 9522.00
Wärmeverlust pro Meter Längenänderung = 267.00
Wärmeverlust pro Meter Breitenänderung = 456.00
Wärmeverlust pro Meter Höhennänderung = 618.00
Aufgabe 5: Lineare Fehlerfortpflanzung#
Für den Radius \(R\) und die Dichte \(\rho\) einer homogenen Kugel wurden die Mittelwerte \(\bar{R} = 12.2\) cm und \(\bar{\rho} = 2.50\) g/cm\(^3\) ermittelt. Eine Schätzung der zugehörigen Messunsicherheiten ergab \(\Delta R = 0.15\) cm und \(\Delta \rho = 0.11\) g/cm\(^3\).
Welche Masse, als indirekt berechneten Mittelwert \(\bar{m}\), besitzt die Kugel?
Mit welchem Maximalwert \(\Delta m_{\text{max}}\) für die Messunsicherheit von \(m\) muss man dabei rechnen?
Wie lautet das Messergebnis für die Masse \(m\)?
Lösung#
Quelle: Papula Band 2, Abschnitt 2.5.5, Übungsaufgabe 35 auf Seite 338
\(m(R,\rho) = \rho V = \rho \frac{4}{3}\pi R^3\), \(\bar{m} = \bar{\rho} \frac{4}{3}\pi \bar{R}^3 = 19015.5\,\text{g} = 19.0155\,\text{kg}\),
\(m = (19.0155 \pm 1.5381)\) kg
Aufgabe 6: Lineare Fehlerfortpflanzung#
Die Leistung eines Gleichstroms wird nach der Formel \(P = RI^2\) berechnet, vgl. Wikipedia: Elektrische Leistung. Widerstand \(R\) und Stromstärke \(I\) wurden in einem Praktikumsversuch wie folgt gemessen:
Geben Sie das Messergebnis für \(P\) an.
Lösung#
Quelle: Papula Klausur- und Übungsaufgaben, Aufgabe E59 auf Seite 275 f.
\(P = (3075 \pm 138)\) W
Aufgabe 7: nicht-lineare Optimierung ohne Nebenbedingungen#
Gesucht ist das Extremum der Funktion \(f(x, y) = 2x^2 - xy - 2y + y^2\). An welcher Stelle befindet es sich, und um welche Art von Extremum handelt es sich?
Lösung#
Quelle: Sanal: Mathematik für Ingenieure. p. 583, Bsp. 11.61
Optimalitätsbedingung \(\nabla f = 0\) liefert einen kritischen Punkt mit \(x = \frac{2}{7}\) und \(y = \frac{8}{7}\). Die Hessematrix von \(f\) ist dort positiv definit, sodass dort ein Minimum vorliegt.
Aufgabe 8: Profitmaximierung, nicht-lineare Optimierung ohne Nebenbedingungen#
Die Energie GmbH investiert 20.000 EUR in das Design und die Entwicklung eines neuen Produkts. Sie kann es für 2 EUR pro Stück herstellen. Wenn die Energie GmbH \(a\) EUR für Marketing ausgibt und das Produkt mit einem Stückpreis von \(p\) EUR anbietet, dann verkauft sie \(2000 + 4\sqrt{a} - 20p\) Stück.
Bestimmen Sie den Profit der Energie GmbH als Funktion \(f(a, p)\).
Bei welchem Stückpreis \(p\) und bei welchen Marketingkosten \(a\) ist der erzielte Profit maximal? Lösen Sie dieses Problem von Hand und numerisch mit Hilfe der Funktion
root.
Lösung#
\(f(a,p) = -20000 + (p - 2)(2000 + 4\sqrt{a} - 20p) - a\)
\(\frac{\partial f}{\partial a}(a,p) = 0\) liefert \(\sqrt{a}=2(p-2)\). \(\frac{\partial f}{\partial p}(a,p) = 0\) liefert \(2040 + 4\sqrt{a} - 40p = 0\) Einsetzen der ersten in die zweite Gleichung liefert \(p = 63.25\) EUR/Stück und \(a = 15006.25\) EUR. Um sich sicher zu sein, dass an dieser Stelle ein Maximum vorliegt, berechnen wir dort die Eigenwerte der Hessematrix \(H = \begin{pmatrix} \frac{2 - p}{\sqrt{a^3}} & \frac{2}{\sqrt{a}} \\ \frac{2}{\sqrt{a}} & -40 \end{pmatrix}\), siehe Code.
p = 63.25
a = 15006.25
H = np.array([[ (2 - p)/a**1.5 , 2/np.sqrt(a)],
[ 2/np.sqrt(a), -40 ]])
print(f"Hessian matrix at critical point = \n{H}.")
L, V = la.eig(H)
print(f"eigenvalues of Hessian matrix at critical point: \n{L}")
Hessian matrix at critical point =
[[-3.33194502e-05 1.63265306e-02]
[ 1.63265306e-02 -4.00000000e+01]].
eigenvalues of Hessian matrix at critical point:
[-2.66555557e-05+0.j -4.00000067e+01+0.j]
def my_grad(x): # gradient, x = [a,p]
a = x[0]
p = x[1]
return [2*(p - 2)/np.sqrt(a) - 1,
2040 + 4*np.sqrt(a) - 40*p]
sol = op.root(my_grad, [3, 3])
print("return value of optimize.root() command: {}".format(sol))
print("solution x = {}".format(sol.x))
return value of optimize.root() command: fjac: array([[-0.04270997, 0.99908751],
[-0.99908751, -0.04270997]])
fun: array([-1.90271354e-10, 1.01226760e-09])
message: 'The solution converged.'
nfev: 74
qtf: array([-7.33736389e-09, -1.05739542e-09])
r: array([ 2.09213765e-02, -5.13968371e+01, 4.47490809e-02])
status: 1
success: True
x: array([15006.25000712, 63.25 ])
solution x = [15006.25000712 63.25 ]
Aufgabe 9: Kontourplot, kritische Punkte, Gradientenfeld#
Gegeben ist die Funktion \(z(x,y) = -x^3 + y^2 + 12x - 6y - 5\).
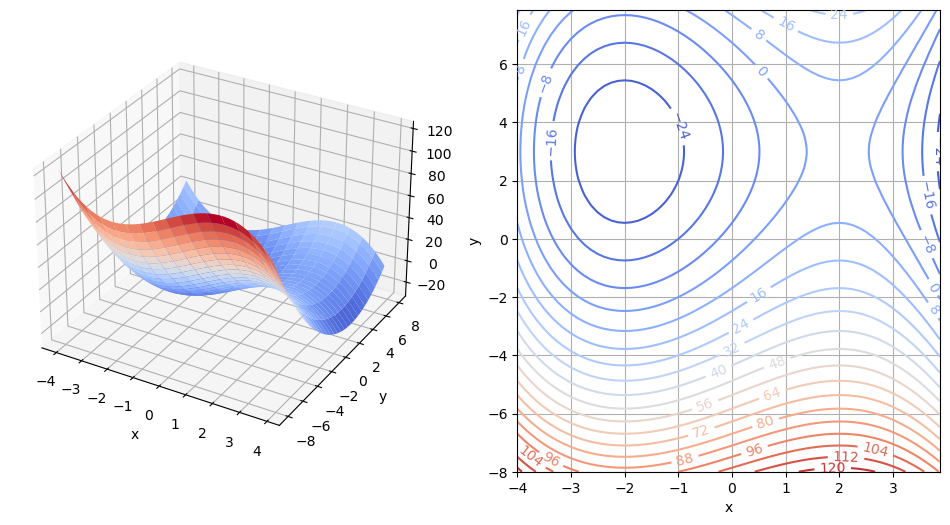
Erstellen Sie den Graphen und den Konturplot von \(z(x,y)\) im Bereich \(x\in[-4,4]\) und \(y\in[-8,8]\).
Finden Sie alle kritischen Punkte von \(z(x,y)\) und bestimmen Sie, welche ein lokales Minimum, Maximum oder Sattelpunkt sind.
Verwenden Sie den Python-Befehl
quiver, um das Gradientenfeld \(\nabla z\) in Ihren Konturplot einzuzeichnen. Hier ein Beispiel dazu für eine andere Funktion:
x = np.arange(0, 3*np.pi, .25)
y = np.arange(0, 3*np.pi, .25)
X,Y = np.meshgrid(x, y)
# Funktion z(x,y)
Z = np.sin(.75*X) - np.cos(Y)
# Gradientenfeld
U = .75*np.cos(.75*X)
V = np.sin(Y)
plt.figure(figsize=(8,6))
CS = plt.contour(X, Y, Z, 15)
Q = plt.quiver(X,Y, U,V)
plt.xlabel('x')
plt.ylabel('y')
Lösung#
x = np.arange(0, 3*np.pi, .25)
y = np.arange(0, 3*np.pi, .25)
X, Y = np.meshgrid(x, y)
# Funktion z(x,y)
Z = np.sin(.75*X) - np.cos(Y)
# Gradientenfeld
U = .75*np.cos(.75*X)
V = np.sin(Y)
plt.figure(figsize=(8,6))
CS = plt.contour(X, Y, Z, 15)
Q = plt.quiver(X,Y, U,V)
plt.xlabel('x')
plt.ylabel('y');
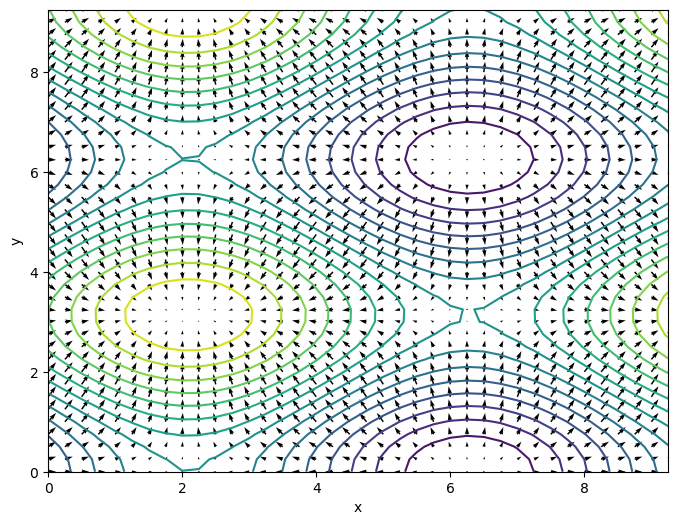
Siehe Code
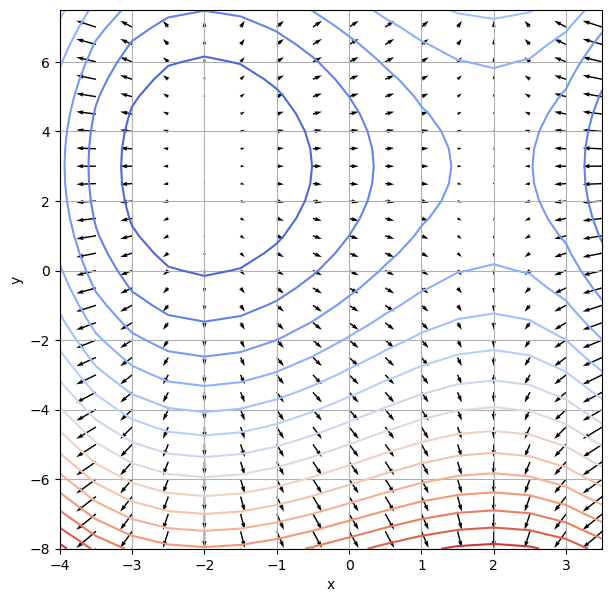
\(\nabla z = 0\) liefert die kritischen Punkte bei \(x= \pm2\) und \(y=3\). Die Hesse-Matrix lautet \(H = \begin{pmatrix} -6x & 0 \\ 0 & 2 \end{pmatrix}\). Ihre Eigenwerte bei \((2,3)\) sind -12 und 2. Daher ist \(H\) bei \((2,3)\) indefinit und \((2,3)\) ist ein Sattelpunkt. Ihre Eigenwerte bei \((-2,3)\) sind 12 und 2. Daher ist \(H\) bei \((2,3)\) positiv definit und \((-2,3)\) ist ein lokales Minimum. Siehe Code.
Siehe Code.
x = np.arange(-4, 4, 0.125)
y = np.arange(-8, 8, 0.125)
X, Y = np.meshgrid(x, y)
Z = -X**3 + Y**2 + 12*X - 6*Y - 5
fig = plt.figure(figsize=(12, 6))
ax = fig.add_subplot(1, 2, 1, projection='3d')
p = ax.plot_surface(X, Y, Z,
rstride=4, cstride=4, linewidth=0, cmap='coolwarm')
ax.view_init(azim=-60, elev=30)
plt.xlabel('x')
plt.ylabel('y')
fig.add_subplot(1, 2, 2)
CS = plt.contour(X, Y, Z, 20, cmap='coolwarm') # colormaps()
plt.clabel(CS, inline=1)
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
H1 = np.array([[-12, 0],
[ 0, 2]])
print(la.eig(H1)[0])
H2 = np.array([[12, 0],
[ 0, 2]])
print(la.eig(H2)[0])
[-12.+0.j 2.+0.j]
[12.+0.j 2.+0.j]
x = np.arange(-4, 4, .5)
y = np.arange(-8, 8, .5)
X, Y = np.meshgrid(x, y)
Z = -X**3 + Y**2 + 12*X - 6*Y - 5
U = -3*X**2 + 12
V = 2*Y - 6
plt.figure(figsize=(7, 7))
CS = plt.contour(X, Y, Z, 15, cmap='coolwarm')
Q = plt.quiver(X, Y, U, V)
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
Aufgabe 10: Design eines Schwimmbeckens, Lagrange-Multiplikatoren#
Ein quaderförmiges Schwimmbecken mit einem Fassungsvermögen (Volumen) von \(V = 108 \text{ m}^3\) soll so gebaut werden, dass die Oberfläche (Boden und Seitenwände) möglichst klein wird. Wie sind die Abmessungen des Beckens zu wählen?
Lösung#
Quelle: Papula: Klausur- und Übungsaufgaben - Auflage 4, Aufgabe E71
Länge \(x\), Breite \(y\), Höhe/Tiefe \(z\). Maximiere \(f(x,y,z) = xy + 2xz + 2yz\) unter \(g(x,y,z) = xyz - 108 = 0\). Die Methode der Lagrange-Multiplikatoren liefert die optimalen Werte \(x=y=2z=6\).
Siehe Lothar Papula: Klausur- und Übungsaufgaben. Auflage 4, Aufgabe E71.
Aufgabe 11: Wärmeverlust in einem Gebäude - Teil 2, Lagrange-Multiplikatoren#
Ein rechteckiges Industriegebäude habe die Länge \(x\), die Breite \(y\) und die Höhe \(z\). In der Tabelle ist der Wärmeverlust pro Tag durch jede Seite des Gebäudes in geeigneten Energieeinheiten pro Quadratmeter Seitenfläche angegeben.
Dach |
Ostseite |
Westseite |
Nordseite |
Südseite |
Boden |
|---|---|---|---|---|---|
10 |
8 |
6 |
10 |
5 |
1 |
Der gesamte tägliche Wärmeverlust des Gebäudes ist daher durch \(Q(x,y,z) = 11xy + 14yz +15xz\) gegeben.
Berechnen Sie die Abmessungen jenes Gebäudes mit einem Volumen von 18480 Kubikmetern, das den minimalen Gesamtwärmeverlust pro Tag hat.
Lösung#
Wir schreiben die Nebenbedingung als \(g(x,y,z) = xyz - 18480 = 0\). Die Optimalitätsbedingung \(\nabla Q = \lambda\nabla g\) liefert das nicht-lineares 3x3-Gleichungssystem
\begin{align} 11y + 15z = & \lambda yz \ 11x + 14z = & \lambda xz \ 14y + 15x = & \lambda xy. \end{align} Freistellen von \(\lambda\) in jeder Gleichung und Gleichsetzen der Terme der ersten mit der zweiten und der zweiten mit der dritten Gleichung liefert \(x=\frac{14}{15}y\) sowie \(z=\frac{11}{15}y\). Einsetzen dieser Zwischenergebnisse in die Nebenbedingung ergibt die Lösung \(x = 28, y = 30, z = 22\).
y = (18480*(15**2)/(14*11))**(1/3)
x = 14/15*y
z = 11/15*y
print(f"{x = :.2f}")
print(f"{y = :.2f}")
print(f"{z = :.2f}")
x = 28.00
y = 30.00
z = 22.00
Aufgabe 12: Produktionsmöglichkeitenkurve und optimaler Produktionsplan, Lagrange-Multiplikatoren#
Ein Unternehmen stellt zwei Produkte A und B her, die das gleiche Rohmaterial verwenden. Das verfügbare Rohmaterial und die verfügbare Arbeitszeit sind begrenzt. Daher muss das Unternehmen entscheiden, wie viel seiner Ressourcen der Produktion von A und wie viel B zugeordnet werden. Es bezeichne \(x\) die Produktionsmenge von A und \(y\) die Produktionsmenge von B. Wir nehmen an, dass die Resourcenbeschränkung folgender Gleichung entspricht:
Die graphische Darstellung dieser Gleichung (für \(x \geq 0\) und \(y \geq 0\)), wird als Produktionsmöglichkeitenkurve bezeichnet. Ein Punkt \((x, y)\) auf dieser Kurve stellt einen Produktionsplan für das Unternehmen dar. Der Grund für die Beziehung zwischen \(x\) und \(y\) beinhaltet die Beschränkungen für die verfügbare Arbeitszeit und das verfügbare Rohmaterial. Wir nehmen zudem an, dass pro Einheit von A ein Gewinn von 3 EUR und pro Einheit von B ein Gewinn von 4 EUR erzielt werden kann.
Zeichnen Sie die Produktionsmöglichkeitenkurve.
Bestimmen Sie den Produktionsplan, der den Gewinn maximiert. Wie hoch ist der maximale Gewinn?
Lösung#
Quelle: Goldstein, Lay, Asmar, Schneider: “Calculus & its Applications”: exercise 13 auf Seite 409
Die Zielfunktion lautet \(f(x,y)=3x+4y\), und die Nebenbedingung scheiben wir als \(g(x,y)=9x^2 + 4y^2 - 18000 = 0\). Die Optimalitätsbedingung \(\nabla f = \lambda\nabla g\) liefert ein lineares Gleichungssystem, dessen Lösung den optimalen Produktionsplan \(x = 20\), \(y = 60\) enthält. Der maximale Gewinn ist \(f(20,60)= 300\) EUR. Siehe Code
l = np.sqrt(5/(4*18000))
x = 1/(6*l)
y = 1/(2*l)
print(f"{x = :.2f}")
print(f"{y = :.2f}")
x = 20.00
y = 60.00
a = np.sqrt(2000)
x = np.linspace(0.1, a - 0.01, 100)
y = 0.5*np.sqrt(18000 - 9*x**2)
delta = 0.25
X, Y = np.meshgrid(x, y)
c = np.array([3, 4])
Z = c[0]*X + c[1]*Y
plt.figure(figsize=(7, 4))
plt.plot(x, y, '-k')
CS = plt.contour(X, Y, Z, cmap='coolwarm')
plt.plot(20, 60, 'or')
plt.xlabel('x')
plt.ylabel('y')
plt.xlim(0, a + 1)
plt.grid(True)

Aufgabe 13: Produktionsmöglichkeitenkurve und optimaler Produktionsplan, Lagrange-Multiplikatoren#
Ein Unternehmen produziert \(x\) Einheiten von Produkt A und \(y\) Einheiten von Produkt B und hat die Produktionsmöglichkeitskurve \(4x^2 + 25y^2 = 50 000\). Die Profite sind 2 EUR pro Einheit von Produkt A und 10 EUR pro Einheit von Produkt B. Bestimmen Sie den Produktionsplan maximalen Gesamtprofits und den dazugehörigen maximalen Gesamtprofit.
Lösung#
Maximiere \(f(x,y) = 2x + 10y\) unter \(g(x,y) = 4x^2 + 25y^2 - 50000 = 0\). Die Methode der Lagrange-Multiplikatoren liefert die optimalen Werte \(x\)=50 und \(y\)=40.
Aufgabe 14: Preisdifferenzierung, nicht-lineare Optimierung mit und ohne Nebenbedingungen#
Eine Firma vermarktet ein Produkt in zwei Ländern mit unterschiedlichen Mengen. Sei \(x\) die Stückzahl, die im ersten Land verkauft werden soll, und \(y\) die Stückzahl, die im zweiten Land verkauft werden soll. Um die Stückzahlen \(x\) und \(y\) vollständig absetzen zu können, muss die Firma den Verkaufspreis im ersten Land auf \(97 - \frac{x}{10}\) EUR/Stück und im zweiten Land auf \(83 - \frac{y}{20}\) EUR/Stück festlegen. Diese Funktionen werden Preis-Absatz-Funktion oder Nachfragefunktion genannt. Die Kosten für die Herstellung betragen \(20000 + 3(x + y)\) EUR.
Bestimmen Sie jene Stückzahlen \(x\) und \(y\), die den Gewinn (= Profit, = Umsatz(=Erlös) minus Kosten) maximieren. Bestimmen Sie diesen maximalen Gewinn.
Angenommen, die Firma muss in jedem Land den selben Preis festlegen, d. h. \(97 -\frac{x}{10} = 83 -\frac{y}{20}\). Bestimmen Sie die Werte von \(x\) und \(y\), die den Gewinn unter dieser Einschränkung maximieren. Bestimmen Sie diesen maximalen Gewinn. Warum ist er niedriger als vorher?
Link: Wikipedia: Preisdifferenzierung
Lösung#
Quelle: Goldstein, Lay, Asmar, Schneider: “Calculus & its Applications”: example 2 auf Seite 397 und exercise 16 auf Seite 409
Die Zielfunktion (Gewinn = Erlös - Kosten) lautet \(f(x,y)= (97 - \frac{x}{10})x + (83 - \frac{y}{20})y - \left[ 20000 + 3(x + y)\right] = 94x - \frac{x^2}{10} + 80y - \frac{y^2}{20} - 20000\). Die Optimalitätsbedingung \(\nabla f = 0\) liefert ein lineares Gleichungssystem, dessen Lösung \(x=470\) und \(y=800\) den einzigen kritischen Punkt ergibt. Die Hesse-Matrix \(H=\begin{pmatrix} -\frac{1}{5} & 0 \\ 0 & -\frac{1}{10} \end{pmatrix}\) ist negativ definit. Daher ist der kritische Punkt \((x,y)=(470,800)\) ein lokales Maximum. Der zugehörige Gewinn \(f(470,800)\) hat den Wert 34090 EUR. Siehe auch Code.
Zur Zielfunktion \(f(x,y) = 94x - \frac{x^2}{10} + 80y - \frac{y^2}{20} - 20000\) kommt noch die Nebenbedingung \(g(x,y) = (97 - \frac{x}{10}) - (83 - \frac{y}{20}) = 0\) dazu. Die Optimalitätsbedingung \(\nabla f = \lambda\nabla g\) liefert ein lineares Gleichungssystem, dessen Lösung die optimalen Werte \(x \simeq 516.7\) und \(y \simeq 753.3\) liefert. Der zugehörige Gewinn hat den niedrigeren Wert von 33763.33 EUR. Siehe auch Code.
def gewinn(x, y):
return (97 - x/10)*x + (83 - y/20)*y - (20000 + 3*(x + y))
print('Aufgabe 1:')
x = 470
y = 800
print(f' {x = :.2f}')
print(f' {y = :.2f}')
print(f' Gewinn = {gewinn(x, y):.2f} EUR')
print('Aufgabe 2:')
lbd = 7*40/3
x = 470 + lbd/2
y = 800 - lbd/2
print(f' {x = :.2f}')
print(f' {y = :.2f}')
print(f' Gewinn = {gewinn(x, y):.2f} EUR')
Aufgabe 1:
x = 470.00
y = 800.00
Gewinn = 34090.00 EUR
Aufgabe 2:
x = 516.67
y = 753.33
Gewinn = 33763.33 EUR
Aufgabe 15: Energieversorgungsnetz, Lagrange-Multiplikatoren#
Drei Generatoren mit folgenden Kostenfunktionen in EUR/Stunde sollen eine Gesamtlast von 952 MW decken.
Die Variable \(x_i\) ist die Ausgangsleistung in MW des \(i\)-ten Generators. Die Funktion \(f_i\) gibt die Kosten pro Stunde des \(i\)-ten Generators an. Die Kostenfunktionen \(f_i\) wurden z.B. durch einen Polynom-Fit basierend auf den historischen Betriebsdaten erstellt.
Berechnen Sie den optimale Generatoreneinsatz, d.h. die optimalen Werte der \(x_i\) Variablen, so dass die Gesamtkosten pro Stunde minimal sind und die Gesamtlast gedeckt ist.
Berechnen Sie die entsprechenden optimalen Gesamtkosten pro Stunde.
Lösung#
Die Zielfunktion lautet \(f(x_1, x_2, x_3) = f_1(x_1) + f_2(x_2) + f_3(x_3)\). Die Nebenbedingung schreiben wir als \(g(x_1, x_2, x_3) = x_1 + x_2 + x_3 - 952 = 0\). Dann liefert die Optimalitätsbedingung \(\nabla f = \lambda\nabla g\) ein lineares Gleichungssystem, dessen Lösung die optimalen Werte der \(x_i\) enthält, siehe Code.
def Kosten(x):
return x[0] + 0.0625*x[0]**2 + x[1] + 0.0125*x[1]**2 + x[2] + 0.0250*x[2]**2
A = np.array([[0.125, 0, 0, -1],
[0, 0.025, 0, -1],
[0, 0, 0.050, -1],
[1, 1, 1, 0]])
b = np.array([-1, -1, -1, 952])
x = la.solve(A, b)
print(f'x = {x[:3]}')
print(f'lambda = {x[3]}')
print(f'Kosten = {Kosten(x[:3]):.2f} EUR/Stunde')
x = [112. 560. 280.]
lambda = 15.0
Kosten = 7616.00 EUR/Stunde
Bemerkung: Der Wert des Lagrange-Multiplikators (auch Schattenpreis genannt) ist die Rate, mit welcher der sich der optimale Zielfunktionswert ändert, wenn man die Randbedingungen ändert:
A = np.array([[0.125, 0, 0, -1],
[0, 0.025, 0, -1],
[0, 0, 0.050, -1],
[1, 1, 1, 0]])
b = np.array([-1, -1, -1, 952 + 1]) # Achtung: 952 + 1
x = la.solve(A, b)
print(f'Kosten = {Kosten(x[:3]):.2f} EUR/Stunde')
Kosten = 7631.01 EUR/Stunde
Aufgabe 16: Ausgleichsgerade#
Nehmen wir an, dass die Werte \(f(x_1)=f_{1},...,f(x_N)=f_N\) bekannt sind, z. B. können sie experimentelle Referenzpunkte sein. Und nehmen wir an, wir wollen die beste lineare Anpassung \(F(x)=ax+b\) an diese Daten finden, die so gut ist, dass der gesamte quadratische Fehler \(E\) minimiert wird
Zeigen Sie
Hinweis: Machen Sie sich klar, dass der Fehler \(E\) von \(a\) und \(b\) abhängt. Differenzieren Sie die Funktion partiell nach \(a\) unb \(b\) und lösen Sie schließlich das resultierende Gleichungssystem. Um Schreibarbeit zu sparen, bietet es sich an, an geeigneter Stelle die Summen durch Buchstaben Ihrer Wahl zu ersetzen.
Lösung#
Wir setzen:
Einsetzen in die oberen Bedingungen liefert
Aus der ersten folgt
Einsezten in die zweite liefert
Einsetzen von b in \(a=\frac{g-bp}{q}\) liefert
Aufgabe 17: Minimale Materialkosten#
Nehmen wir an, wir wollen eine zylindrische Suppendose aus Blech mit einem Preis von \(\alpha\) Cent pro Flächeneinheit und einem vorgegebenen Volumen \(V\) entwerfen, wobei die Materialkosten minimiert werden sollen. Wenn \(x\) der Radius und \(y\) die Höhe ist, haben wir das Optimierungsproblem
mit der Nebenbedingung
Skizieren Sie die zylindrische Dose mit Radius \(x\) und Höhe \(y\). Überlegen Sie sich, wie die Kostenfunktion und die Nebenbedingung zustande kommen.
Lösen Sie \(x\) und \(y\) mit der Eliminationsmethode, und zeigen Sie, dass \(x = \sqrt[3]{ \frac{V}{2\pi} }\) und \(y = 2 \sqrt[3]{ \frac{V}{2\pi} }\) ist.
Lösen Sie \(x\) und \(y\) mit der Lagrange-Methode.
Lösung#
ad 1.:
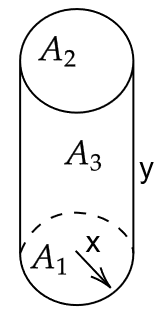
ad 2.:
ad 3.:
Aus dieser Bedingung können die folgenden zwei Gleichungen gewnonnen werden
Aus der zweiten folgt
Einsetzen in die erste liefert
Einsetzten von \(x\) und \(y\) in die Nebenbedingung \(V=\pi x^2y\) liefert dann
Einsetzten von \(\lambda\) in die oberen Gleichungen für \(x\) und \(y\) ergibt schließlich
Aufgabe 18: Lagrange-Multiplikatoren, Konturplot#
Gegeben sei die folgende Aufgabe:
Lösen Sie das Problem mit der Methode der Lagrange-Multiplikatoren.
Plotten Sie die durch die Nebenbedingung erlaubte Menge an \((x, y)\)-Punkten, die Höhenlinien der Zielfunktion und die Gradienten der Zielfunktion und der Nebenbedingung (jeweils als Pfeil dargestellt) im Optimum. Interpretieren und beschreiben Sie diesen Plot.
Hinweis: Verwenden Sie für die Höhenlinien die Funktion countour und für die Pfeildarstellung arrow aus matplotlib.pyplot.
Lösung#
# 1)
# x = 1/sqrt(2) , y = 1/sqrt(2)
# 2)
x = np.linspace(-3, 4, 200)
y = np.linspace(-3, 4, 200)
X, Y = np.meshgrid(x, y)
F = X + Y
CS = plt.contour(X, Y, F, 10)
plt.clabel(CS, inline=True, fontsize=10)
def circ(x, u):
return u*np.sqrt(1 - x**2)
x = np.linspace(-1 , 1, 100)
plt.plot(x, circ(x, 1), "g")
plt.plot(x, circ(x, -1), "g");
plt.arrow(1/np.sqrt(2), 1/np.sqrt(2), 1, 1,
linewidth = 1.5, color='black', head_width=0.2)
plt.arrow(1/np.sqrt(2), 1/np.sqrt(2), 2*(1/np.sqrt(2)), 2*(1/np.sqrt(2)),
linewidth = 1.5, color='red', head_width=0.2)
plt.plot(1/np.sqrt(2), 1/np.sqrt(2), "rx", label="Optimum")
plt.xlabel("x")
plt.ylabel("y")
plt.axis("equal")
plt.legend();
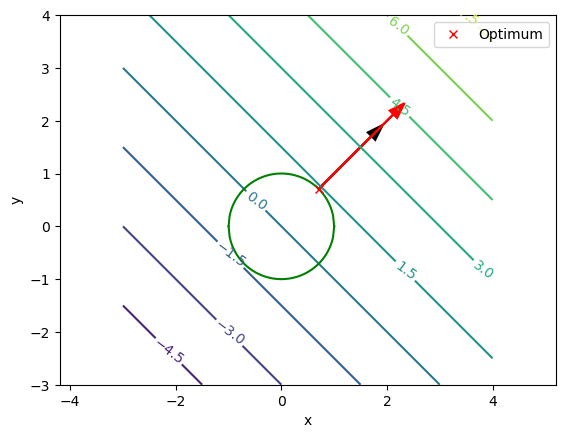
Aufgabe 19: Optimale Beleuchtung#
Ein fester Punkt \(A\) einer ebenen Bühne wird durch eine in der Höhe \(h\) verstellbare punktförmige Lichtquelle \(L\) mit der konstaten Lichstärke \(I_0\) beleuchtet.
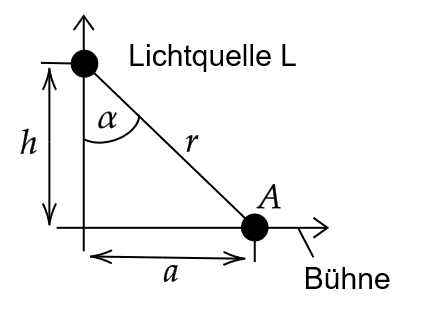
Die von der Lichtquelle \(L\) im Punkt \(A\) erzeugte Beleuchtungsstärke \(B\) genügt dabei dem Lambertschen Gesetz
\(\alpha\) ist der Einfallswinkel des Lichtes, \(r\) der Abstand zwischen der Lichtquelle \(L\) und dem Bühnenpunkt \(A\) und \(a\) der Abstand des Bühnenpunktes \(A\) vom Fußpunkt der Lichtquelle \(L\). Unter welchem Winkel \(\alpha\) wird dieser Punkt optimal beleuchtet?
Hinweis: Finden Sie eine Beziehung zwischen \(\alpha\) und \(r\) (dies ist dann Ihre Nebenbedingung). Wenden Sie dann die Methode der Lagrange-Multiplikatoren an, um das Problem zu lösen. \(\frac{\sin(\alpha)}{\cos(\alpha)} = \tan(\alpha)\) könnte ebenfalls hilfreich sein.
Lösung#
Aus der Grafik etnehmen wir \(\sin(\alpha) = \frac{a}{r} \implies r\sin(\alpha) - a = 0\). Das ist unsere Nebenbedingung. Am Optimum ist der Gradient der Zielfunktion ein skalares vielfaches des Gradienen der Nebenbedingung, daher:
Damit haben wir:
Aufgabe 20: Fermatsches Prinzip#
Es sei eine Lichtquelle an einem Punkt \(A\) in einem Medium, in dem die Lichtgeschwindigkeit \(v_1\) ist, gegeben. Von den von \(A\) ausgehenden Strahlen interessiert uns derjenige, der an einem gegebenen Punkt \(B\) in einem zweiten Medium ankommt, in dem die Lichtgeschwindigkeit \(v_2\) ist, wobei die Grenzfläche zwischen den beiden Medien die Ebene \(P\) ist.
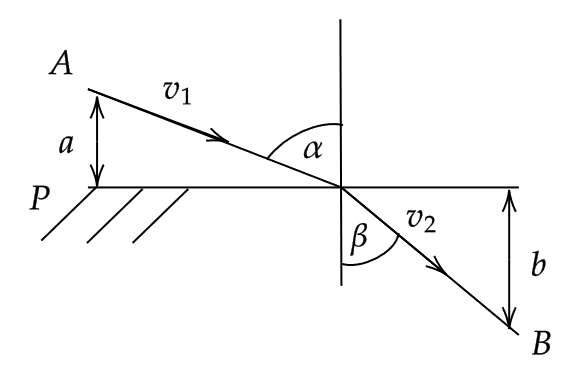
Fermats Grundprinzip der Optik besagt, dass von allen möglichen Wegen derjenige tatsächlich beschritten wird, der so beschaffen ist, dass die Zeit \(T\) von \(A\) nach \(B\) ein Minimum ist, daher:
Lösen Sie dieses Problem mit der Methode der Lagrange-Multiplikatoren und leiten Sie daraus das Brechungsgesetz \(\frac{\sin(\alpha)}{\sin(\beta)} = \frac{v_1}{v_2}\) ab .
Lösung#
Aufgabe 21: Minimaler Materialverbrauch#
Wie muss man den Öffnungswinkel \(\alpha\) eines kegelförmigen Trichters vom Volumen \(V_0 = 10\) dm\(^3\) wählen, damit der Materialverbrauch für die Mantelfläche möglichst klein wird?
Hinweis: Der Mantel soll aus einem homogenen Blech konstanter Dicke hergestellt werden. Verwenden Sie die Methode der Lagrange-Multiplikatoren und stellen Sie die Zielfunktion und die Nebenbedingung als Funktion des Radius \(r\) und des Winkels \(\alpha\) dar.

Lösung#
Wir deffinieren \(\beta := \frac{\alpha}{2}\). Aus der Skizze entnehmen wir \(\sin(\beta) = \frac{r}{s}\) und \(\tan(\beta) = \frac{r}{h}\). Das Volumen des Kegels ist gegeben durch \(V = \frac{1}{3}h\pi r^2\) und die Matelfläche durch \(M = \pi r s\). Dies gibt die Zielfunktion und die Nebenbedingung als:
Am Optimum ist der Gradient der Zielfunktion ein skalares Vielfaches des Gradienten der Nebenbedingung, damit gilt:
Daraus gewinnen wir:
also

