Aufgaben#

Python-Pakete und Konfiguration#

import numpy as np
import scipy.linalg as la  # or: from scipy import linalg as la
import scipy.optimize as op
import matplotlib.pyplot as plt

%matplotlib inline

# set default values for all plotting:
plt.rcParams['axes.titlesize']  = 14
plt.rcParams['axes.labelsize']  = 14
plt.rcParams['xtick.labelsize'] = 14
plt.rcParams['ytick.labelsize'] = 14
plt.rcParams['legend.fontsize'] = 12
plt.rcParams['lines.linewidth'] = 2

Aufgabe 1: Partielle Ableitungen, ideales Gas, ÖPNV#

  1. Ideales Gas: Das Volumen \(V\) einer bestimmten Menge eines idealen Gases ist durch die Temperatur \(T\) und den Druck \(p\) über die Formel \(V = 0.08\frac{T}{p}\) gegeben. Berechnen und interpretieren Sie \(\frac{\partial V}{\partial p}\) und \(\frac{\partial V}{\partial T}\) bei \(p = 20\) und \(T = 300\).

  2. Öffentlicher Personennahverkehr: In einer Vorstadt haben Pendler die Möglichkeit mit dem Bus oder mit dem Zug in das Stadtzentrum zu kommen. Die Nachfrage nach diesen Verkehrsarten variiert mit ihrer Kosten. Sei \(B(b, z)\) die Anzahl der Menschen, die mit dem Bus fahren wird, wenn \(b\) der Preis für den Bus und \(z\) der Preis der Zug sind. Zum Beispiel: Bei \(B(4, 6) = 7000\) nehmen 7000 Pendler den Bus, wenn der Preis den Bus \(4\) ist und der Preis für den Zug \(6\) ist. Erklären Sie, warum \(\frac{\partial B}{\partial b} <0\) und \(\frac{\partial B}{\partial z}> 0\) gelten.

Aufgabe 2: Wärmeleitungsgleichung#

Zeigen Sie, dass die Temperaturfunktion

\[T(x,t)= \frac{1}{\sqrt{t}}e^{-\frac{x^2}{4t}}\]

die Wärmeleitungsgleichung

\[\frac{\partial T}{\partial t}(x,t)= \frac{\partial^2 T}{\partial x^2}(x,t)\]

erfüllt. Plotten Sie die örtliche Temperaturverteilung für einige verschiedene Zeiten. Interpretieren Sie die Wärmeleitungsgleichung und die spezielle Lösung \(T(x,t)\).

Aufgabe 3: lineare Approximation und Funktionswertdifferenz#

Berechnen Sie das Differential der Funktion \(f:\mathbb{R}^2 \rightarrow\mathbb{R}: z(x, y) = e^{-(3x^2 + y^2)}\) allgemein und im Speziellen bei \((x_0, y_0)=(1,2)\). Wie groß ist der Unterschied zwischen der linearen Approximation \(\text{d}z\) der Funktionswertdifferenz und der wahren Funktionswertdifferenz \(\Delta z\) bei \((x_0, y_0)\), wenn \(\text{d}x = 0.1\) und \(\text{d}y = -0.2\)?

Aufgabe 4: Wärmeverlust in einem Gebäude - Teil 1, partielle Ableitungen#

Ein rechteckiges Industriegebäude habe die Länge \(x\), die Breite \(y\) und die Höhe \(z\). In der Tabelle ist der Wärmeverlust pro Tag durch jede Seite des Gebäudes in geeigneten Energieeinheiten pro Quadratmeter Seitenfläche angegeben.

Dach

Ostseite

Westseite

Nordseite

Südseite

Boden

10

8

6

10

5

1

Der gesamte tägliche Wärmeverlust des Gebäudes sei mit Sei \(Q(x, y, z)\) bezeichnet.

  1. Finden Sie eine Formel für \(Q(x, y, z)\).

  2. Geben Sie den gesamten täglichen Wärmeverlust an, wenn das Gebäude 30 Meter lang, 12 Meter breit und 9 Meter hoch ist.

  3. Berechnen und interpretieren Sie \(\frac{\partial Q}{\partial x} (30, 12, 9)\), \(\frac{\partial Q}{\partial y}(30, 12, 9)\) und \(\frac{\partial Q}{\partial z} (30, 12, 9)\).

Aufgabe 5: Lineare Fehlerfortpflanzung#

Für den Radius \(R\) und die Dichte \(\rho\) einer homogenen Kugel wurden die Mittelwerte \(\bar{R} = 12.2\) cm und \(\bar{\rho} = 2.50\) g/cm\(^3\) ermittelt. Eine Schätzung der zugehörigen Messunsicherheiten ergab \(\Delta R = 0.15\) cm und \(\Delta \rho = 0.11\) g/cm\(^3\).

  1. Welche Masse, als indirekt berechneten Mittelwert \(\bar{m}\), besitzt die Kugel?

  2. Mit welchem Maximalwert \(\Delta m_{\text{max}}\) für die Messunsicherheit von \(m\) muss man dabei rechnen?

  3. Wie lautet das Messergebnis für die Masse \(m\)?

Aufgabe 6: Lineare Fehlerfortpflanzung#

Die Leistung eines Gleichstroms wird nach der Formel \(P = RI^2\) berechnet, vgl. Wikipedia: Elektrische Leistung. Widerstand \(R\) und Stromstärke \(I\) wurden in einem Praktikumsversuch wie folgt gemessen:

\[\begin{split}\begin{align} R &= (80.0 \pm 1.0) \,\Omega \\ I &= ( 6.2 \pm 0.1) \,\text{A} \end{align}\end{split}\]

Geben Sie das Messergebnis für \(P\) an.

Aufgabe 7: nicht-lineare Optimierung ohne Nebenbedingungen#

Gesucht ist das Extremum der Funktion \(f(x, y) = 2x^2 - xy - 2y + y^2\). An welcher Stelle befindet es sich, und um welche Art von Extremum handelt es sich?

Aufgabe 8: Profitmaximierung, nicht-lineare Optimierung ohne Nebenbedingungen#

Die Energie GmbH investiert 20.000 EUR in das Design und die Entwicklung eines neuen Produkts. Sie kann es für 2 EUR pro Stück herstellen. Wenn die Energie GmbH \(a\) EUR für Marketing ausgibt und das Produkt mit einem Stückpreis von \(p\) EUR anbietet, dann verkauft sie \(2000 + 4\sqrt{a} - 20p\) Stück.

  1. Bestimmen Sie den Profit der Energie GmbH als Funktion \(f(a, p)\).

  2. Bei welchem Stückpreis \(p\) und bei welchen Marketingkosten \(a\) ist der erzielte Profit maximal? Lösen Sie dieses Problem von Hand und numerisch mit Hilfe der Funktion root.

Aufgabe 9: Kontourplot, kritische Punkte, Gradientenfeld#

Gegeben ist die Funktion \(z(x,y) = -x^3 + y^2 + 12x - 6y - 5\).

  1. Erstellen Sie den Graphen und den Konturplot von \(z(x,y)\) im Bereich \(x\in[-4,4]\) und \(y\in[-8,8]\).

  2. Finden Sie alle kritischen Punkte von \(z(x,y)\) und bestimmen Sie, welche ein lokales Minimum, Maximum oder Sattelpunkt sind.

  3. Verwenden Sie den Python-Befehl quiver, um das Gradientenfeld \(\nabla z\) in Ihren Konturplot einzuzeichnen. Hier ein Beispiel dazu für eine andere Funktion:

x = np.arange(0, 3*np.pi, .25)
y = np.arange(0, 3*np.pi, .25)
X,Y = np.meshgrid(x, y)

# Funktion z(x,y)
Z = np.sin(.75*X) - np.cos(Y)

# Gradientenfeld
U = .75*np.cos(.75*X)
V = np.sin(Y)

plt.figure(figsize=(8,6))
CS = plt.contour(X, Y, Z, 15)
Q = plt.quiver(X,Y, U,V)
plt.xlabel('x')
plt.ylabel('y')

Aufgabe 10: Design eines Schwimmbeckens, Lagrange-Multiplikatoren#

Ein quaderförmiges Schwimmbecken mit einem Fassungsvermögen (Volumen) von \(V = 108 \text{ m}^3\) soll so gebaut werden, dass die Oberfläche (Boden und Seitenwände) möglichst klein wird. Wie sind die Abmessungen des Beckens zu wählen?

Aufgabe 11: Wärmeverlust in einem Gebäude - Teil 2, Lagrange-Multiplikatoren#

Ein rechteckiges Industriegebäude habe die Länge \(x\), die Breite \(y\) und die Höhe \(z\). In der Tabelle ist der Wärmeverlust pro Tag durch jede Seite des Gebäudes in geeigneten Energieeinheiten pro Quadratmeter Seitenfläche angegeben.

Dach

Ostseite

Westseite

Nordseite

Südseite

Boden

10

8

6

10

5

1

Der gesamte tägliche Wärmeverlust des Gebäudes ist daher durch \(Q(x,y,z) = 11xy + 14yz +15xz\) gegeben.

Berechnen Sie die Abmessungen jenes Gebäudes mit einem Volumen von 18480 Kubikmetern, das den minimalen Gesamtwärmeverlust pro Tag hat.

Aufgabe 12: Produktionsmöglichkeitenkurve und optimaler Produktionsplan, Lagrange-Multiplikatoren#

Ein Unternehmen stellt zwei Produkte A und B her, die das gleiche Rohmaterial verwenden. Das verfügbare Rohmaterial und die verfügbare Arbeitszeit sind begrenzt. Daher muss das Unternehmen entscheiden, wie viel seiner Ressourcen der Produktion von A und wie viel B zugeordnet werden. Es bezeichne \(x\) die Produktionsmenge von A und \(y\) die Produktionsmenge von B. Wir nehmen an, dass die Resourcenbeschränkung folgender Gleichung entspricht:

\[9x^2 + 4y^2 = 18 000.\]

Die graphische Darstellung dieser Gleichung (für \(x \geq 0\) und \(y \geq 0\)), wird als Produktionsmöglichkeitenkurve bezeichnet. Ein Punkt \((x, y)\) auf dieser Kurve stellt einen Produktionsplan für das Unternehmen dar. Der Grund für die Beziehung zwischen \(x\) und \(y\) beinhaltet die Beschränkungen für die verfügbare Arbeitszeit und das verfügbare Rohmaterial. Wir nehmen zudem an, dass pro Einheit von A ein Gewinn von 3 EUR und pro Einheit von B ein Gewinn von 4 EUR erzielt werden kann.

  1. Zeichnen Sie die Produktionsmöglichkeitenkurve.

  2. Bestimmen Sie den Produktionsplan, der den Gewinn maximiert. Wie hoch ist der maximale Gewinn?

Aufgabe 13: Produktionsmöglichkeitenkurve und optimaler Produktionsplan, Lagrange-Multiplikatoren#

Ein Unternehmen produziert \(x\) Einheiten von Produkt A und \(y\) Einheiten von Produkt B und hat die Produktionsmöglichkeitskurve \(4x^2 + 25y^2 = 50 000\). Die Profite sind 2 EUR pro Einheit von Produkt A und 10 EUR pro Einheit von Produkt B. Bestimmen Sie den Produktionsplan maximalen Gesamtprofits und den dazugehörigen maximalen Gesamtprofit.

Aufgabe 14: Preisdifferenzierung, nicht-lineare Optimierung mit und ohne Nebenbedingungen#

Eine Firma vermarktet ein Produkt in zwei Ländern mit unterschiedlichen Mengen. Sei \(x\) die Stückzahl, die im ersten Land verkauft werden soll, und \(y\) die Stückzahl, die im zweiten Land verkauft werden soll. Um die Stückzahlen \(x\) und \(y\) vollständig absetzen zu können, muss die Firma den Verkaufspreis im ersten Land auf \(97 - \frac{x}{10}\) EUR/Stück und im zweiten Land auf \(83 - \frac{y}{20}\) EUR/Stück festlegen. Diese Funktionen werden Preis-Absatz-Funktion oder Nachfragefunktion genannt. Die Kosten für die Herstellung betragen \(20000 + 3(x + y)\) EUR.

  1. Bestimmen Sie jene Stückzahlen \(x\) und \(y\), die den Gewinn (= Profit, = Umsatz(=Erlös) minus Kosten) maximieren. Bestimmen Sie diesen maximalen Gewinn.

  2. Angenommen, die Firma muss in jedem Land den selben Preis festlegen, d. h. \(97 -\frac{x}{10} = 83 -\frac{y}{20}\). Bestimmen Sie die Werte von \(x\) und \(y\), die den Gewinn unter dieser Einschränkung maximieren. Bestimmen Sie diesen maximalen Gewinn. Warum ist er niedriger als vorher?

Link: Wikipedia: Preisdifferenzierung

Aufgabe 15: Energieversorgungsnetz, Lagrange-Multiplikatoren#

Drei Generatoren mit folgenden Kostenfunktionen in EUR/Stunde sollen eine Gesamtlast von 952 MW decken.

\[\begin{split}\begin{align} f_1(x_1) &= x_1 + 0.0625 x_1^2 \\ f_2(x_2) &= x_2 + 0.0125 x_2^2 \\ f_3(x_3) &= x_3 + 0.0250 x_3^2 \end{align}\end{split}\]

Die Variable \(x_i\) ist die Ausgangsleistung in MW des \(i\)-ten Generators. Die Funktion \(f_i\) gibt die Kosten pro Stunde des \(i\)-ten Generators an. Die Kostenfunktionen \(f_i\) wurden z.B. durch einen Polynom-Fit basierend auf den historischen Betriebsdaten erstellt.

  1. Berechnen Sie den optimale Generatoreneinsatz, d.h. die optimalen Werte der \(x_i\) Variablen, so dass die Gesamtkosten pro Stunde minimal sind und die Gesamtlast gedeckt ist.

  2. Berechnen Sie die entsprechenden optimalen Gesamtkosten pro Stunde.

Aufgabe 16: Ausgleichsgerade#

Nehmen wir an, dass die Werte \(f(x_1)=f_{1},...,f(x_N)=f_N\) bekannt sind, z. B. können sie experimentelle Referenzpunkte sein. Und nehmen wir an, wir wollen die beste lineare Anpassung \(F(x)=ax+b\) an diese Daten finden, die so gut ist, dass der gesamte quadratische Fehler \(E\) minimiert wird

\[E(a,b)=\sum_{j=1}^{N}(F(x)-f_{j})^2 \rightarrow \min\]

Zeigen Sie

\[a=\frac{N\sum_{j=1}^{N}x_jf_j-(\sum_{j=1}^{N}f_j)(\sum_{j=1}^{N}x_j)}{N\sum_{j=1}^{N}x_{j}^2-(\sum_{j=1}^{N}x_j)^2}\]
\[b=\frac{(\sum_{j=1}^{N}x_j^2)(\sum_{j=1}^{N}f_j)-(\sum_{j=1}^{N}x_j)(\sum_{j=1}^{N}x_jf_j)}{N\sum_{j=1}^{N}x_{j}^2-(\sum_{j=1}^{N}x_j)^2}\]

Hinweis: Machen Sie sich klar, dass der Fehler \(E\) von \(a\) und \(b\) abhängt. Differenzieren Sie die Funktion partiell nach \(a\) unb \(b\) und lösen Sie schließlich das resultierende Gleichungssystem. Um Schreibarbeit zu sparen, bietet es sich an, an geeigneter Stelle die Summen durch Buchstaben Ihrer Wahl zu ersetzen.

Aufgabe 17: Minimale Materialkosten#

Nehmen wir an, wir wollen eine zylindrische Suppendose aus Blech mit einem Preis von \(\alpha\) Cent pro Flächeneinheit und einem vorgegebenen Volumen \(V\) entwerfen, wobei die Materialkosten minimiert werden sollen. Wenn \(x\) der Radius und \(y\) die Höhe ist, haben wir das Optimierungsproblem

\[f(x,y)=\alpha(2\pi x^2+2\pi xy) \rightarrow \min\]

mit der Nebenbedingung

\[V=\pi x^2y\]

  1. Skizieren Sie die zylindrische Dose mit Radius \(x\) und Höhe \(y\). Überlegen Sie sich, wie die Kostenfunktion und die Nebenbedingung zustande kommen.

  2. Lösen Sie \(x\) und \(y\) mit der Eliminationsmethode, und zeigen Sie, dass \(x = \sqrt[3]{ \frac{V}{2\pi} }\) und \(y = 2 \sqrt[3]{ \frac{V}{2\pi} }\) ist.

  3. Lösen Sie \(x\) und \(y\) mit der Lagrange-Methode.

Aufgabe 18: Lagrange-Multiplikatoren, Konturplot (2 Punkte)#

Gegeben sei die folgende Aufgabe:

\[\begin{split} \max x + y \\ \text{s.t. } x^2 + y^2 = 1\end{split}\]

  1. Lösen Sie das Problem mit der Methode der Lagrange-Multiplikatoren.

  2. Plotten Sie die durch die Nebenbedingung erlaubte Menge an \((x, y)\)-Punkten, die Höhenlinien der Zielfunktion und die Gradienten der Zielfunktion und der Nebenbedingung (jeweils als Pfeil dargestellt) im Optimum. Interpretieren und beschreiben Sie diesen Plot.

Hinweis: Verwenden Sie für die Höhenlinien die Funktion countour und für die Pfeildarstellung arrow aus matplotlib.pyplot.

Aufgabe 19: Optimale Beleuchtung (2 Punkte)#

Ein fester Punkt \(A\) einer ebenen Bühne wird durch eine in der Höhe \(h\) verstellbare punktförmige Lichtquelle \(L\) mit der konstaten Lichstärke \(I_0\) beleuchtet.

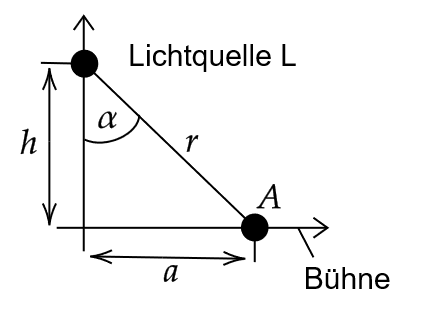
BspLicht.png

Die von der Lichtquelle \(L\) im Punkt \(A\) erzeugte Beleuchtungsstärke \(B\) genügt dabei dem Lambertschen Gesetz

\[B(\alpha, r) = \frac{I_0 \cos(\alpha)}{r^2}\]

\(\alpha\) ist der Einfallswinkel des Lichtes, \(r\) der Abstand zwischen der Lichtquelle \(L\) und dem Bühnenpunkt \(A\) und \(a\) der Abstand des Bühnenpunktes \(A\) vom Fußpunkt der Lichtquelle \(L\). Unter welchem Winkel \(\alpha\) wird dieser Punkt optimal beleuchtet?

Hinweis: Finden Sie eine Beziehung zwischen \(\alpha\) und \(r\) (dies ist dann Ihre Nebenbedingung). Wenden Sie dann die Methode der Lagrange-Multiplikatoren an, um das Problem zu lösen. \(\frac{\sin(\alpha)}{\cos(\alpha)} = \tan(\alpha)\) könnte ebenfalls hilfreich sein.

Aufgabe 20: Fermatsches Prinzip (2 Punkte)#

Es sei eine Lichtquelle an einem Punkt \(A\) in einem Medium, in dem die Lichtgeschwindigkeit \(v_1\) ist, gegeben. Von den von \(A\) ausgehenden Strahlen interessiert uns derjenige, der an einem gegebenen Punkt \(B\) in einem zweiten Medium ankommt, in dem die Lichtgeschwindigkeit \(v_2\) ist, wobei die Grenzfläche zwischen den beiden Medien die Ebene \(P\) ist.

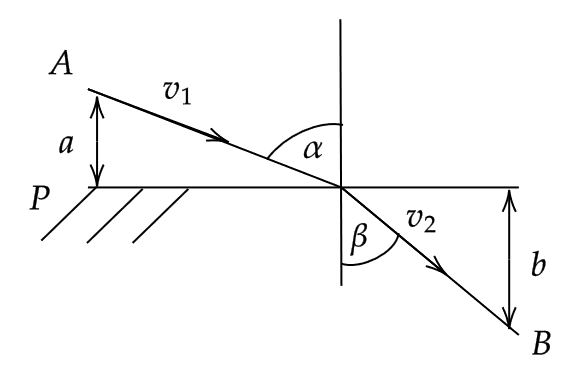
Brechungsgesetz.png

Fermats Grundprinzip der Optik besagt, dass von allen möglichen Wegen derjenige tatsächlich beschritten wird, der so beschaffen ist, dass die Zeit \(T\) von \(A\) nach \(B\) ein Minimum ist, daher:

\[T(\alpha, \beta) = \frac{a}{v_1 \cos(\alpha)} + \frac{b}{v_2 \cos(\beta)} \rightarrow \text{Minimum}\]
\[g(\alpha, \beta) = a \tan(\alpha) + b \tan(\beta) = \text{konstant}\]

Lösen Sie dieses Problem mit der Methode der Lagrange-Multiplikatoren und leiten Sie daraus das Brechungsgesetz \(\frac{\sin(\alpha)}{\sin(\beta)} = \frac{v_1}{v_2}\) ab .

Aufgabe 21: Minimaler Materialverbrauch (2 Punkte)#

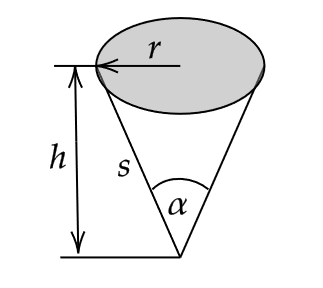
Wie muss man den Öffnungswinkel \(\alpha\) eines kegelförmigen Trichters vom Volumen \(V_0 = 10\) dm\(^3\) wählen, damit der Materialverbrauch für die Mantelfläche möglichst klein wird?

Hinweis: Der Mantel soll aus einem homogenen Blech konstanter Dicke hergestellt werden. Verwenden Sie die Methode der Lagrange-Multiplikatoren und stellen Sie die Zielfunktion und die Nebenbedingung als Funktion des Radius \(r\) und des Winkels \(\alpha\) dar.

Trichter2.png