Lineare Optimierung - Übungen
Contents
Lineare Optimierung - Übungen¶
%pylab inline
%config InlineBackend.figure_format = 'svg'
from scipy.optimize import linprog
%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib
Aufgaben¶
Aufgabe LO1: Förster¶
Dieses Beispiel stammt aus dem Buch Linear Programming von Vasek Chvatal. Ein Förster hat 100 Hektar Wald mit Hartholz und hat folgende zwei Möglichkeiten.
Option 1: Bestehende Hartholzbestände fällen und anschließende Regeneration, Kosten 10 EUR/ha, Erlös 50 EUR/ha
Option 2: Bestehende Hartholzbestände fällen und anschließend mit Pinien aufforsten, Kosten 50 EUR/ha, Erlös 120 EUR/ha
Die daraus resultiernden Gewinne sind 40 EUR/ha und 70 EUR/ha. Er hat momentan 4000 EUR zur Verfügung.
Formulieren Sie das lineare Problem (LP) der Profitmaximierung.
Lösen Sie das LP mit graphischen Mitteln durch händisches Rechnen.
Lösen Sie das LP in Python mit der Funktion
linprog, die Sie mit folgendem Befehl importieren können:
from scipy.optimize import linprog
Aufgabe LO2: Produktionsplanung¶
Gegeben seien 2 Produkte A und B, die aus dem Rohstoffen R\(_1\), R\(_2\), und R\(_3\) hergestellt werden können. Untenstehende Tabelle zeigt die für die Produktion nötigen Mengen zur Herstellung einer Einheit des jeweiligen Produkts sowie die zur Verfügung stehende Menge an Rohstoffen.
Rohstoff |
Produkt A |
Produkt B |
verfügbare Menge |
|---|---|---|---|
R\(_1\) |
5 |
10 |
3000 |
R\(_2\) |
0 |
3 |
750 |
R\(_3\) |
4 |
2 |
1200 |
Der erwirtschaftete Profit für eine Einheit des Produkts A ist 200 EUR und 300 EUR für Produkt B.
Formulieren Sie das lineare Problem (LP) der Profitmaximierung.
Lösen Sie das LP mit graphischen Mitteln durch händisches Rechnen.
Lösen Sie das LP in Python mit der Funktion
linprog.
Aufgabe LO3: Kupfer-Zinn Legierung mit minimalen Kosten¶
Drei Klassen Altmetall werden geschmolzen, um 200 kg Kupfer-Zinn Legierung zu erhalten.
Klasse 1 enthält 80% Kupfer, 20% Zinn und kostet EUR 6 pro kg.
Klasse 2 enthält 40% Kupfer, 60% Zinn und kostet EUR 3 pro kg.
Klasse 3 enthält 10% Kupfer, 90% Zinn und kostet EUR 4 pro kg.
Die Legierung soll maximal 60% Kupfer und 50% Zinn enthalten.
Formulieren Sie das lineare Problem (LP) der Kostenminimierung.
Lösen Sie das LP in Python mit der Funktion
linprog.
Aufgabe LO4: Fluss in einem Netzwerk¶
Das folgende Beispiel stammt aus dem Buch Matousek, Gärtner: Understanding and Using Linear Programming. Springer 2007, section 2.2 p. 14ff.
Betrachten Sie den Graphen in der Abbildung unten, der beispielsweise ein Energie- oder Informationsnetzwerk modellieren könnte. Er hat die Knoten \(s\) (Quelle), \(a\), \(b\), \(c\), \(d\), \(e\) und \(t\) (Ziel). Die Knoten \(a\), \(b\), \(c\), \(d\) und \(e\) können keine Energie bzw. Information zwischenspeichern. Die Kanten haben die angegeben Kapazitäten (= maximale Transferraten).
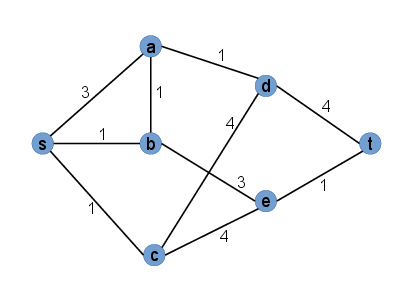
Berechnen Sie in Python mit Hilfe eines LP die maximale Energie- bzw. Informationsübertragungsrate vom Knoten \(s\) zum Knoten \(t\).
Aufgabe LO5: Personaleinsatzplanung¶
Dieses Problem stammt von der folgenden Online-Sammlung von LP-Problemen http://www.me.utexas.edu/~jensen/ORMM/models/unit/linear/index.html.
Betrachten wir ein Busunternehmen, das eine optimale Personaleinsatzplanung erstellen möchte. Der Bedarf an Bussen variiert, wie in folgender Abbildung dargestellt, aufgrund der Kundennachfrage von Stunde zu Stunde:
periods = arange(0, 24, 4)
buses = array([4, 8, 10, 7, 12, 4])
figure(figsize=(5,3))
bar(periods, buses, width=4, color='lightgray')
xticks(periods)
xlabel('Tageszeit')
ylabel('Bedarf an Bussen')
grid(True)
Beispielsweise müssen vier Busse von Mitternacht bis 4 Uhr im Einsatz sein, während acht Busse von 4 bis 8 Uhr fahren müssen. Wir gehen davon aus, dass die Nachfrage jeden Tag die gleiche ist.
Sie sollen bestimmen, wie viele Fahrer für jede Startzeit bei Bedarfsdeckung einzuplanen sind. Fahrer arbeiten in 8-Stundenschichten, die um 0, 4, 8, 12, 16 oder 20 Uhr beginnen. Zum Beispiel kann ein Fahrer ab 0 Uhr einen Bus bis 8 Uhr fahren. Ein Fahrer, der um 20 Uhr zu arbeiten beginnt, fährt die letzten vier Stunden des Tages und die ersten vier Stunden des nächsten Tags. Das Ziel besteht darin, die Anzahl der eingesetzten Fahrer und somit die Kosten zu minimieren. Beachten Sie, dass, obwohl ein Fahrer für einen Zeitraum von acht Stunden eingesetzt werden kann, es nicht erforderlich ist, dass er für den gesamten Zeitraum einen Bus fährt. Er könnte auch für vier Stunden innerhalb seines Zeitraums pausieren.
Eine zulässige Entscheidung für dieses Problem besteht darin, 8 Fahrer zum Zeitpunkt 0, 10 Fahrer zum Zeitpunkt 8 und 12 Fahrer zum Zeitpunkt 16 einzusetzen. Diese Entscheidung deckt alle Anforderungen ab und verwendet insgesamt 30 Fahrer, ist aber nicht optimal. Das Problem besteht darin, die kleinst mögliche Anzahl an Fahrern zu finden.
Lösen Sie das LP in Python.
Aufgabe LO6: Tierfuttermischung¶
Sie sollen die optimalen Mengen von drei Zutaten in einer Tierfuttermischung bestimmen. Das Endprodukt hat mehrere Nährstoffbedingungen zu erfüllen. Die möglichen Zutaten, ihre Nährstoffe (in kg Nährstoff pro kg Zutat) und die Zutatenpreise (in EUR pro Kilogramm) sind in der folgenden Tabelle dargestellt.
Zutat |
Kalzium |
Eiweiß |
Balaststoffe |
Preis |
|---|---|---|---|---|
Kalk |
0.380 |
0.00 |
0.00 |
10.0 |
Getreide |
0.001 |
0.09 |
0.02 |
30.5 |
Sojamehl |
0.002 |
0.50 |
0.08 |
90.0 |
Die Mischung muss die folgenden Bedingungen erfüllen:
Kalzium: mindestens 0.8 %, aber nicht mehr als 1.2 %
Eiweiß: mindestens 22 %
Balaststoffe: höchstens 5 %
Das Problem besteht darin, jene Zusammensetzung der Futtermittelmischung zu finden, die die Nebenbedingungen erfüllt und die Kosten minimiert. Formulieren Sie diese Problem als LP in der Form:
Aufgabe LO7: Zulässigkeitsbereich, Konturlinien, optimaler Wert und optimale Punkte¶
Zeichnen Sie den Zulässigkeitsbereich für folgende Nebenebedingungen \(x_1 + 2x_2 \leq 6\), \(2x_1 + x_2 \leq 6\), \(x_1 \geq 0\), \(x_2 \geq 0\).
Zeichnen Sie die Konturlinien der Profitfunktion \(f(x) = 2x_1 + 4x_2\).
Ermitteln Sie grafisch den optimalen Wert und alle optimalen Punkte des LP, die die Profitfunktion unter den Nebenbedingungen maximieren.
Aufgabe LO8: Zulässigkeitsbereich, Konturlinien, optimaler Wert und optimale Punkte¶
Zeichnen Sie den Zulässigkeitsbereich für folgende Nebenebedingungen \(-2x_1 + x_2 \leq 1\), \(x_1 + 3x_2 \geq 2\), \(x_1 \geq 0\), \(x_2 \geq 0\)
Zeichnen Sie die Konturlinien der Kostenfunktion \(f(x) = 3x_1 + 2x_2\).
Ermitteln Sie grafisch den optimalen Wert und alle optimalen Punkte des LP, die die Kostenfunktion unter den Nebenbedingungen minimieren.
Aufgabe LO9: Energiespeicheroptimierung¶
Sie haben 24 Stunden Zeit, um einem Kunden \(E\)=300 kWh Energie zur Verfügung zu stellen, indem Sie ihm einen anfänglich leeren Energiespeicher befüllen. Die maximale Einspeisleistung beträgt \(P\)=20kW, und Energie kann nicht aus dem Speicher zurück ins Energieversorgungsnetz geführt werden. Die Energiepreise sind für jede Stunde durch \(c_1, c_2, ..., c_{24}\) gegeben. Der Speicher hat einen Wirkungsgrad von 90 %, d. h. 90 % der in den Speicher eingespeisten Energie kann der Kunde tatsächlich nutzen.
Formulieren Sie das Optimerungsproblem, das die gesamtkostenoptimalen Einspeiseenergien für jede Stunde liefert.
Aufgabe L1O: Separation von Erzen¶
Erz aus drei verschiedenen Minen wird von einer Firma vor dem Weitertransport in drei unterschiedliche Güteklassen separiert. Die täglichen Produktionskapazitäten der Minen und ihre täglichen Betriebskosten sind in der folgenden Tabelle angeführt.
Mine |
Tonnen/Tag hohe Güte |
Tonnen/Tag niedrige Güte |
Betriebskosten/Tag in 1000 EUR |
|---|---|---|---|
Mine 1 |
4 |
4 |
20 |
Mine 2 |
6 |
4 |
22 |
Mine 3 |
1 |
6 |
18 |
Die Firma muss mindestens 54 Tonnen Erz hoher Güte und mindestens 65 Tonnen Erz niedriger Güte pro Woche liefern. Gesucht sind die Betriebstage pro Woche für jede Mine, sodass die Firma ihre Lieferversprechen bei minimalen Kosten einhält.
Formulieren Sie dieses lineare Problem in Matrixform.
Quelle: Schaum’ Outlines: Operations Research, Aufgabe 1.5, S. 5
Lösungen¶
Lösung LO1: Förster¶
\(x_1\): Fläche, die mit Option 1 bewirtschaftet wird
\(x_2\): Fläche, die mit Option 2 bewirtschaftet wird
# Zielfunktion:
c = array([-40, -70])
# Ungleichungsnebenbedingungen:
A = array([[ 10, 50]])
b = array([4000])
# Gleichungsnebenbedingungen:
G = array([[ 1, 1]])
h = array([100])
res = linprog(c, A_ub=A, b_ub=b, A_eq= G, b_eq=h, bounds= (0, None))
print("Resultate:\n", res)
Resultate:
con: array([2.4069753e-05])
fun: -6249.998487942359
message: 'Optimization terminated successfully.'
nit: 4
slack: array([0.00097305])
status: 0
success: True
x: array([24.99999424, 74.99998169])
Lösung LO2: Produktionsplanung¶
\(x_1\): Menge von Produkt A
\(x_2\): Menge von Produkt B
# Zielfunktion:
c = array([-200, -300])
# Ungleichungsnebenbedingungen:
A = array([[ 5, 10],
[ 0, 3],
[ 4, 2]])
b = array([3000, 750, 1200])
res = linprog(c, A_ub=A, b_ub=b, bounds= (0, None))
print("Resultate:\n", res)
Resultate:
con: array([], dtype=float64)
fun: -99999.99989263291
message: 'Optimization terminated successfully.'
nit: 5
slack: array([3.22073811e-06, 1.50000001e+02, 1.28884426e-06])
status: 0
success: True
x: array([199.99999979, 199.99999979])
Lösung LO3: Kupfer-Zinn Legierung mit minimalen Kosten¶
\(x_1\): kg von Klasse 1
\(x_2\): kg von Klasse 2
\(x_3\): kg von Klasse 3
# Zielfunktion:
c = array([6, 3, 4])
# Ungleichungsnebenbedingungen:
A = array([[ .8, .4, .1],
[ .2, .6, .9]])
b = array([200*0.6, 200*0.5])
# Gleichungsnebenbedingungen:
G = array([[1, 1, 1]])
h = array([200])
res = linprog(c, A_ub=A, b_ub=b, A_eq= G, b_eq=h, bounds= (0, None))
print("Resultate:\n", res)
Resultate:
con: array([3.55107616e-06])
fun: 749.9999871004075
message: 'Optimization terminated successfully.'
nit: 5
slack: array([2.00000017e+01, 1.80638654e-06])
status: 0
success: True
x: array([4.99999992e+01, 1.49999997e+02, 5.71014209e-08])
Lösung LO4: Fluss in einem Netzwerk¶
Der Fluß durch eine Kante vom Knoten \(m\) zum Konten \(n\) wird durch eine Variable \(x_{mn}\) modelliert. Der Gesamtfluß aus der Quelle oder der Gesamtfluß in das Ziel wird maximiert. Für jeden Knoten hat man die Gleichungsnebenbedingung, dass der Gesmtfluß in den Knoten Null sein muss. Für jede Kante hat man durch die Kapazitäten zwei Ungleichungsnebenbedingungen, die den maximalen Fluß in jede Richtung beschränken.
# sa, sb, sc, ab, ad, be, ce, cd, dt, et
c = array([-1, -1, -1, 0, 0, 0, 0, 0, 0, 0 ])
# sa, sb, sc, ab, ad, be, ce, cd, dt, et
G = array([[ 1, 0, 0, -1, -1, 0, 0, 0, 0, 0],
[ 0, 1, 0, 1, 0, -1, 0, 0, 0, 0],
[ 0, 0, 1, 0, 0, 0, -1, -1, 0, 0],
[ 0, 0, 0, 0, 1, 0, 0, 1, -1, 0],
[ 0, 0, 0, 0, 0, 1, 1, 0, 0, -1]])
h = array([0, 0, 0, 0, 0])
res = linprog(c, A_eq= G, b_eq=h,
bounds= [(-3,3), (-1,1), (-1,1), (-1,1), (-1,1),
(-3,3), (-4,4), (-4,4), (-4,4), (-1,1)])
print("Resultate:\n", res)
Resultate:
con: array([ 5.95120020e-09, -5.95118532e-09, -1.78535853e-08, 8.88178420e-16,
1.48779795e-08])
fun: -3.9999999506566035
message: 'Optimization terminated successfully.'
nit: 5
slack: array([], dtype=float64)
status: 0
success: True
x: array([ 1.99999998, 0.99999999, 0.99999999, 1. , 0.99999998,
1.99999998, -1.42569831, 2.42569828, 3.42569827, 0.57430168])
Lösung LO5: Personaleinsatzplanung¶
Definition der Entscheidungsvariabeln: \(x_i\) … Anzahl Fahrer, die in Periode \(i = 1, 2, ...,6\) zu arbeiten beginnen.
Zielfunktion: min \(x_1 + x_2 + x_3 + x_4 + x_5 +x_6\)
Nebenbedingungen:
c = ones(6)
print("c:\n", c)
A = -eye(6,dtype = 'int') - eye(6,k=-1)
A[0,5] = -1
b = -array([4,8,10,7,12,4])
print("A:\n", A)
print("b:\n", b)
res = linprog(c, A_ub=A, b_ub=b, bounds=(0,None))
print("Resultate:\n", res)
c:
[1. 1. 1. 1. 1. 1.]
A:
[[-1. 0. 0. 0. 0. -1.]
[-1. -1. 0. 0. 0. 0.]
[ 0. -1. -1. 0. 0. 0.]
[ 0. 0. -1. -1. 0. 0.]
[ 0. 0. 0. -1. -1. 0.]
[ 0. 0. 0. 0. -1. -1.]]
b:
[ -4 -8 -10 -7 -12 -4]
Resultate:
con: array([], dtype=float64)
fun: 25.999999515780907
message: 'Optimization terminated successfully.'
nit: 4
slack: array([-6.70094162e-08, 1.93238823e+00, -2.32314058e-07, 2.49446166e+00,
-1.84895617e-07, 2.57314963e+00])
status: 0
success: True
x: array([2.23593566, 7.69645256, 2.3035472 , 7.19091445, 4.80908536,
1.76406427])
figure(figsize=(7,3))
periods = arange(0,24,4)
subplot(1,2,1)
bar(periods, -b, width=4, color='lightgray', align='edge')
xticks(periods)
grid(True)
subplot(1,2,2)
stem(periods + 2, res.x, use_line_collection=True)
grid(True)
Lösung LO6: Tierfuttermischung¶
\(x_1\) Menge an Kalk in kg
\(x_2\) Menge an Getreide in kg
\(x_3\) Menge an Sojamehl in kg
Konvention: Da keine Gesamtmenge für die Tierfuttermischung vorgegeben ist, verwenden wir ohne Einschränkung der Allgemeinheit eine Gesamtmenge von 1 kg. Die numerischen Werte des Optimums von \(x_1, x_2, x_3\) können dadurch auch als Anteile interpretiert werden.
Zielfunktion: Minimieren von \(10 x_1 + 30.5 x_2 + 90 x_3\)
Nebenbedingungen:
\(x_1 + x_2 + x_3 = 1\)
\(0.008 \leq 0.38 x_1 + 0.001 x_2 + 0.002 x_3 \leq 0.012\)
\(0.22 \leq 0.09 x_2 + 0.05 x_3\)
\(0.02 x_2 + 0.08 x_3 \leq 0.05\)
\(x_k \geq 0\) für alle \(k=1,2,3\)
Matrixform:
\(c = (10, 30.5, 90)\), \(G = (1, 1, 1)\), \(h = 1\), \(A = \begin{pmatrix} 0.38 & 0.001 & 0.002 \\ -0.38 & -0.001 & -0.002 \\ 0.0 & -0.09 & -0.05 \\ 0.0 & 0.02 & 0.08 \\ -1.0 & 0.0 & 0.0 \\ 0.0 & -1.0 & 0.0 \\ 0.0 & 0.0 & -1.0 \\ \end{pmatrix}\), \(b = \begin{pmatrix} 0.012 \\ -0.008 \\ -0.22 \\ 0.05 \\ 0 \\ 0 \\ 0 \end{pmatrix}\)
Lösung LO7: Zulässigkeitsbereich, Konturlinien, optimaler Wert und optimale Punkte¶
Siehe Code
Siehe Code
Alle Punkte auf der Strecke von (0,3) nach (2,2) sind optimal und liefern den optimalen Wert von 12.
c = -array([ 2, 4])
A = array([[ 1, 2],
[ 2, 1]])
b = array([6, 6])
linprog(c, A_ub=A, b_ub=b, bounds=(0, None))
con: array([], dtype=float64)
fun: -11.999999999992038
message: 'Optimization terminated successfully.'
nit: 4
slack: array([3.98081568e-12, 1.20307377e+00])
status: 0
success: True
x: array([1.19795082, 2.40102459])
ecken = array([[0,0],
[3,0],
[2,2],
[0,3]])
delta = 1
x1 = arange(-1, 8, delta)
x2 = arange(-1, 8, delta)
X1, X2 = meshgrid(x1, x2)
p = array([2, 4])
Z = p[0]*X1 + p[1]*X2
fig = figure(figsize=(6,6))
ax = fig.add_subplot(111)
ax.add_patch(Polygon(ecken, closed=True, color='green', alpha=0.3))
arrow(0, 0, p[0], p[1], head_width=0.2, fc='k')
CS = contour(X1, X2, Z, levels= linspace(0, 24, 13), cmap= 'coolwarm')
clabel(CS, inline=1, fontsize=12, fmt='%1.1f')
xlim(-1,5)
ylim(-1,5)
xlabel('$x_1$')
ylabel('$x_2$')
grid(True)
Lösung LO8: Zulässigkeitsbereich, Konturlinien, optimaler Wert und optimale Punkte¶
Siehe Code
Siehe Code
Der Punkte (0,2/3) ist optimal und liefert den optimalen Wert von 4/3.
ecken = array([[7,15],
[0,1],
[0,2/3],
[2,0],
[9,0]])
delta = 1
x1 = arange(-1, 8, delta)
x2 = arange(-1, 8, delta)
X1, X2 = meshgrid(x1, x2)
p = array([3, 2])
Z = p[0]*X1 + p[1]*X2
fig = figure(figsize=(6,6))
ax = fig.add_subplot(111)
ax.add_patch(Polygon(ecken, closed=True, color='green', alpha=0.3))
arrow(0, 0, p[0], p[1], head_width=0.2, fc='k')
CS = contour(X1, X2, Z, levels= linspace(-1,19, 20), cmap= 'coolwarm')
clabel(CS, inline=1, fontsize=12, fmt='%1.1f')
xlim(-1,4)
ylim(-1,4)
xlabel('$x_1$')
ylabel('$x_2$')
grid(True)
Lösung LO9: Energiespeicheroptimierung¶
\(t\) = 1,2,3, …, 24 … Stunde
\(x_t\) … eingespeiste Energie [kWh] in der Stunde \(t\)
Zielfunktion: Minimieren von \(\sum_{t=1}^{24} c_t x_t\)
Nebenbedingungen:
\(0 \leq x_t \leq 20\)
\(\sum_{t=1}^{24} x_t = 300/0.9\)
Lösung L1O: Separation von Erzen¶
Kurztestfragen¶
Ein LP-Solver liefert als Rückgabe die Meldung The LP is infeasible (Anm. deutsch: unzulässig). Was schließen Sie über den zulässigen Bereich des LP?
Ein LP-Solver liefert als Rückgabe die Meldung Optimal value = 123.45. Wieviele Lösungen hat das LP?
Erklären Sie den Begriff Schattenpreis.
Ein LP-Solver liefert als Rückgabe die Meldung The LP is unbounded (Anm. deutsch: unbeschränkt). Was schließen Sie über den zulässigen Bereich des LP?
Erklären Sie die Begriffe “Polyeder” und “optimale Menge eines LP”?
Bringen Sie das LP max. \(3x_1 + 4x_2\) s. t. \(x_1 + x_2 = 1\) und \(2x_1 - 3x_2 \geq 6\) in die Ungleichungsform min. \(c^T x\) s. t. \(Ax \leq b\), d. h., bestimmen Sie \(c\), \(A\) und \(b\).
Bringen Sie das LP max. \(x_1 + x_2\) s. t. \(3x_1 - x_2 \geq 1\) und \(2x_1 + x_2 \leq 6\) in die Ungleichungsform min. \(c^T x\) s. t. \(Ax \leq b\), d. h., bestimmen Sie \(c\), \(A\) und \(b\).
Welche mögliche Lösungsstrukturen (Anzahl der Lösungen und zugehöriger optimaler Wert) haben lineare Optimierungen min \(c^Tx\) s. t. \(Ax\leq b\)?
Ein LP-Solver liefert als Rückmeldung The LP is unbounded (deutsch: unbeschränkt). Welche Aussage können Sie über den zulässigen Bereich treffen, und was ist der optimale Wert des linearen Optimierungsproblems bei einer Minimierung der Zielfunktion?
Wie viele Lösungen kann ein lineares Optimierungsproblem mit Nebenbedingungen \(Ax\leq b\) haben?
Ein Mobilfunkbetreiber möchte seinen monatlichen Gewinn durch einen neuen Handytarif maximieren. Zum Tarif Speedy um 10 EUR/Monat kommt der Tarif Basic um 5 EUR/Monat dazu. Wie lautet die Zielfunktion des linearen Optimierungsproblems bei einer Formulierung als Minimierungsproblem min. \(c^T x\)?
Für beide Tarife aus Aufgabe 11) wird ein monatliches Datenvolumen von 5 GB angeboten. Die vertraglich zugesicherte Downloadgeschwindigkeit beträgt beim Tarif Speedy 30 Mbit/s und beim Tarif Basic 5 Mbit/s. Beim Tarif Speedy sind darüber hinaus 4 GB EU-Datenroaming inkludiert. Der Mobilfunkbetreiber kann ingesamt ein monatliches Datenvolumen von maximal 1000 GB, eine maximale Downloadgeschwindigkeit von 2000 Mbit/s sowie bis zu 240 GB EU-Datenroaming bereitstellen. Formulieren Sie sämtliche Nebenbedingungen des linearen Optimierungsproblems in der Form \(Ax\leq b\).
Lösen Sie das in den Aufgaben 11) und 12) definierte lineare Optimierungsproblem graphisch. Zeichnen Sie den Punkt ein, bei dem sich für den Mobilfunkbetreiber der maximale monatliche Gewinn ergibt. Sollten Sie Aufgabe 4) nicht lösen können, lösen Sie in dieser Aufgabe stattdessen das lineare Optimierungsproblem, das durch das nachfolgende Ungleichungssystem und die Zielfunktion aus Aufgabe 3) gegeben ist:
Programmierprojekte¶
KWK im flexiblen Strommarkt¶
Ein KWK-Heizkraftwerk hat folgende Daten:
Nennleistung thermisch bei 100 % Auslastung: 19.2 MW
Nennleistung elektrisch bei 100 % Auslastung: 5.0 MW
Die Auslastung darf nie unter 30 % sinken und nie 100 % übersteigen.
Zwischen 8:00 und 20:00 Uhr muss die Auslastung bei mindestens 50 % liegen.
Der Heizkessel kann in einer Stunde gleichmäßig von 30 % Auslastung auf 100 % hochgefahren werden.
Für das gleichmäßige Herunterfahren des Kessels von 100 % auf 30 % Auslastung werden 30 Minuten benötigt.
Die Betreiberfirma des KWK hat sich verpflichtet, täglich in Summe 250 MWh thermische Energie in ein Fernwärmenetzwerk einzuspeisen. Die elektrische Energie wird am Strommarkt zu den 1/4-Stunden-Day-Ahead-Preisen der EXAA verkauft.
Aufgaben:
Formulieren Sie das Optimierungsproblem, das einen optimalen Auslastungsfahrplan für den maximalen Ertrag aus dem Stromverkauf eines Tages liefert?
Lösen Sie das Optimierungsproblem für 3 verschiedene Tage im Jahre 2016 und stellen Sie die Ergebnisse grafisch dar.
Abgabe: Hochladen eines Ipython-Notebook als ipynb-Datein und aller evtl. zusätzlichen (Daten-)Files in ILIAS.
Lösung:
Entscheidungsvariablen: Auslastungen \(x_k\) für \(k=1,\ldots, 96\) in den 1/4-Stunden beginnend zu den Zeiten \(t_k=0, \ldots, 23.75\).
Zielfunktion: Max. \(p^Tx\) für 1/4-Stundenpreise \(p_k\)
Nebenbedingungen:
\(0.3 \leq x_k \leq 1\)
\(0.5 \leq x_k\) für Zeiten zw. 8 und 20 Uhr
\(-0.35 \leq x_k - x_{k-1} \leq 0.175\)
\(19.2\cdot 0.25\cdot \sum_k x_k = 250\)
# Zeiten:
dt = .25 # Delta Zeit
Zeit = arange(0, 24, dt) # [0, ..., 23.75]
Zp = len(Zeit) # Anzahl Zeitpunkte
# Zielfunktion:
Preise = genfromtxt('daten/dshistory2016_.csv',delimiter=';', usecols=range(1,4*24+1))
Preis = Preise[1,:]
figure(figsize=(6,3))
plot(Zeit, Preis, 'o-')
xlabel('Zeit [h]')
ylabel('Strompreis [EUR/MWh]')
grid(True)
c = -Preis
# 00 - 08 Uhr: 8*4 Zeitpunkte
# 08 - 20 uhr: 12*4 Zeitpunkte
# 20 - 24 Uhr: 4*4 Zeitpunkte
A1 = zeros((12*4, 8*4))
A2 = -eye(12*4)
A3 = zeros((12*4, 4*4))
A_ub = hstack((A1, A2, A3))
b_ub = -0.5*ones((12*4, 1))
A4 = eye(Zp - 1, Zp) - eye(Zp - 1, Zp, k=1)
A5 = -A4
b4 = 0.175*ones((Zp - 1, 1))
b5 = 0.350*ones((Zp - 1, 1))
A_ub = vstack((A_ub, A4, A5))
b_ub = vstack((b_ub, b4, b5))
A_eq = 19.2*dt*ones((1, Zp))
b_eq = array([250])
res = linprog(c, # Zielfunktion, die minimiert wird
A_ub, b_ub, # Nebenbedingungen: Ungleichungen <=
A_eq, b_eq, # Nebenbedingungen: Gleichungen =
bounds=(0.3, 1.0), # Nebenbedingungen: Variablenschranken l <= x_n <= u
options={"disp": True}
)
Primal Feasibility Dual Feasibility Duality Gap Step Path Parameter Objective
1.0 1.0 1.0 - 1.0 -4107.346
0.2329373569783 0.2329373569783 0.2329373569783 0.7717088604003 0.2329373569783 -3890.310563724
0.08836020411116 0.08836020411116 0.08836020411116 0.6581591078129 0.08836020411116 -2464.532440912
0.04121939780893 0.04121939780893 0.04121939780893 0.5536361307905 0.04121939780893 -2068.066490588
0.02388150960973 0.02388150960973 0.02388150960973 0.4361009587697 0.02388150960973 -1940.744764824
0.008844784334876 0.008844784334875 0.008844784334875 0.6502409712552 0.008844784334875 -1830.238324579
0.003356323239483 0.003356323239483 0.003356323239483 0.6336063035584 0.003356323239483 -1790.685946561
0.0002790772723485 0.0002790772723479 0.0002790772723478 0.9291667208372 0.0002790772723495 -1768.72518623
5.934980081596e-06 5.934980084133e-06 5.93498008413e-06 0.9790977804557 5.934980076835e-06 -1766.784307049
3.346091237568e-10 3.346078517201e-10 3.346079055637e-10 0.9999436381023 3.346117127033e-10 -1766.7423357
Optimization terminated successfully.
Current function value: -1766.742336
Iterations: 9
print("Maximaler Ertrag aus Stromverkauf = %.2f EUR" %(-res['fun']))
x = res['x']
figure(figsize=(7,3))
plot(Zeit, Preis,'o-r')
vlines([8, 20], 0, max(Preis), linestyles='--', colors='r')
xlabel('Zeit [h]')
ylabel('Strompreis [EUR/MWh]')
grid(True)
figure(figsize=(7,3))
plot(Zeit, x*100,'o-k', label= 'Auslastung')
vlines([8, 20], 0, 1.1, linestyles='--', colors='k')
xlabel('Zeit [h]')
ylabel('%')
ylim(0, 110)
grid(True)
Maximaler Ertrag aus Stromverkauf = 1766.74 EUR
Checks:
print(min(diff(x)))
print(max(diff(x)))
print(A_eq@x)
-0.17500000065076227
0.35000000014835697
[250.00000033]
Optimierung von Produktionsabläufen via LP¶
Ein befreundeter Unternehmensberater steht vor der Herausforderung, die Produktionsabläufe eines Kunden zu erfassen. Leider sind seine Kenntnisse in Powerpoint deutlich besser als die in Linearer Algebra, weswegen er Sie um Hilfe beim Aufstellen und Lösen der zu Grunde liegenden mathematischen Optimierung bittet. Folgende Daten aus der Produktion des Unternehmens teilt er Ihnen mit:
Das Unternehmen fertigt zurzeit mit zwei Maschinen die Produkte P1, P2 und P3 . Die Absatzpreise betragen 10 EUR für P1, 20 EUR für P2 und 15 EUR für P3.
Auf Maschine 1 können P1 und P2 gefertigt werden. Die Fertigung von P1 auf Maschine 1 verbraucht 2 Arbeitsstunden, während P2 3 Stunden benötigt.
Maschine 2 kann P1 und P3 produzieren, für beide Produkte sind dabei jeweils 4 Arbeitsstunden aufzuwenden.
Auf Maschine 2 produzierte Einheiten von P1 benötigen keine weitere Bearbeitung auf Maschine 1. Umgekehrt gilt, dass auf Maschine 1 produzierte Einheiten von P1 keine weitere Bearbeitung durch Maschine 2 benötigen.
Im betrachteten Zeitraum sind 1.000 Arbeitsstunden auf Maschine 1 eingeplant, auf Maschine 2 das doppelte Arbeitsstundenbudget. Aus tariflichen Gründen muss beachtet werden, dass mindestens zwei Drittel der Gesamtproduktionsmenge von P1 auf Maschine 1 gefertigt wird. Aus der Marketingabteilung kommt aufgrund von geplanten Werbekampagnen die Auflage, dass der Anteil von P3 an der Gesamtproduktion (gemessen an der Stückmenge der produzieren Einheiten) höchstens ein Drittel betragen darf.
Aufgaben:
Formulieren Sie ein vollständiges LP zur Erlösmaximierung in Matrixform.
Lösen Sie das LP unter Python mit dem Solver
linprog.Bestimmen Sie die Schattenpreise mit Hilfe des dualen LP, und interpretieren Sie sie.
Abgabe: Hochladen eines Ipython-Notebook als ipynb-Datei in ILIAS.
Lösung:
Quelle: Mayer, Weber, Francas: Lineare Algebra für Wirtschaftswissenschaftler. 6. Auflage. Aufgabe 8.12, S. 204f., Lösung S. 308
Entscheidungsvariablen:
\(x_1\) := Produktionsmenge P1 auf Maschine 1
\(x_2\) := Produktionsmenge P1 auf Maschine 2
\(x_3\) := Produktionsmenge P2
\(x_4\) := Produktionsmenge P3
ZielfunktionF: max. \(10(x_1 + x_2) + 20x_3 + 15x_4\)
NB:
\(2x_1 + 3x_3 \leq 1000\)
\(4x_2 + 4x_4 \leq 2000\)
\(x_1 \geq 2/3 (x_1 + x_2)\)
\(x_4 \leq 1/3 (x_1 + x_2 + x_3 + x_4)\)
\(x_1, x_2, x_3, x_4 \geq 0\)
# Min.-Zielfunktion:
c = array([-10, -10, -20, -15])
# Ungleichungsnebenbedingungen:
A = array([[ 2, 0, 3, 0],
[ 0, 4, 0, 4],
[-1/3, 2/3, 0, 0],
[-1/3,-1/3,-1/3,2/3]
])
b = array([1000, 2000, 0, 0])
res = linprog(c, A_ub=A, b_ub=b, bounds= (0, None))
print("Resultate:\n", res)
Resultate:
con: array([], dtype=float64)
fun: -12045.454544333561
message: 'Optimization terminated successfully.'
nit: 6
slack: array([ 9.27930159e-08, 1.87040769e-07, 9.78133130e-11, -5.82929260e-11])
status: 0
success: True
x: array([363.6363636 , 181.8181818 , 90.9090909 , 318.18181815])
Dem primären LP in Ungleichungsform
entspricht das duale LP
Die Werte des \(z\)-Lösungsvektors sind die Schattenpreise.
A = array([[ 2, 0, 3, 0],
[ 0, 4, 0, 4],
[-1/3, 2/3, 0, 0],
[-1/3,-1/3,-1/3,2/3],
[ -1, 0, 0, 0],
[ 0, -1, 0, 0],
[ 0, 0, -1, 0],
[ 0, 0, 0, -1]
])
b = array([1000, 2000, 0, 0,
0, 0, 0, 0
])
res = linprog(b, A_eq=A.T, b_eq=-c)
res
con: array([8.95612473e-10, 6.18316065e-10, 1.69640657e-09, 1.04498987e-09])
fun: 12045.45454456917
message: 'Optimization terminated successfully.'
nit: 6
slack: array([], dtype=float64)
status: 0
success: True
x: array([7.72727273e+00, 2.15909091e+00, 6.81818182e+00, 9.54545454e+00,
1.44193552e-11, 3.50744964e-11, 1.05654929e-10, 5.72394885e-11])
Speicheroptimierung¶
Wir betrachten folgende, vereinfachte Speicheranwendung eines Prosumers im elektrischen Netz:

Die Pfeile geben jene Richtungen an, in die ein Energiefuss positiv gezählt wird. Es wird vereinfachend angenommen, dass die selben Preise für Einspeisung in das Netz und Abnahme vom Netz gelten.
Wir verwenden folgende Einheiten:
Zeit: h
Leistung, Last: kW
Energie: kWh
Kosten und Erlös: EUR
Wir wollen einen optimalen Speicher-Lastfahrplan für die kommenden Stunden bestimmen. Dazu betrachten wir sechs zukünftige Zeitperioden von jeweils einer Stunde, die wir mit ihren Anfangszeitpunkten \(t = 0, 1, 2, ... , 5\) indizieren. In jeder Periode \(t\) wird jede Last als konstant modelliert:
\(x_t\) … Leistung in den Speicher, Entscheidungsvariablen
\(d_t\) … Prosumerlast in den Haushalt, gegeben
\(n_t\) … Leistung aus dem Netz, ergibt sich aus \(x_t\) und \(d_t\)
Der Speicher kann in jeder Periode mit max. \(p_{\text{max}} = 2\) kW ge- oder entladen werden und wird als verlustlos angenommen. Der Speicher hat einen minimalen Speicherstand von \(E_{\text{min}} = 0\) kWh und einen maximalen Speicherstand von \(E_{\text{max}} = 6\) kWh. Zum Anfangszeitpunkt \(t=0\) ist der Speicherstand mit \(E_{\text{Anfang}} = 2.5\) kWh bekannt. Zum Endzeitpunkt \(t=6\) muss der Speicherstand \(E_{\text{Ende}} = 2.5\) kWh betragen.
Die Prosumerlast \(d_t\) und die stündlichen Energiepreise \(c_t\) in EUR/kWh für die Netzlast werden als bekannt angenommen und haben folgende Werte:
d = array([0.5, -1.0 , -0.5 , 1.5 , 1.5 , 0.5])
c = array([0.1, 0.08, 0.08, 0.12, 0.11, 0.12])
Aufgaben:
Bestimmen Sie mittels eines Linearen Programms einen Speicherlast-Fahrplan mit minimalen Kosten für die resultierende Netzlast. Stellen Sie alle Lasten und den Speicherstand im Verlauf der Zeit dar. Wie groß ist die Kosteneinsparung durch die optimierte Verwendung des Speichers im Vergleich zu ohne Speicher?
Bestimmen Sie einen Speicherlast-Fahrplan mit minimaler maximaler absoluter Netzlast. Damit ist gemeint, dass die maximale Netzlast, vom oder in das Netz, über die sechs Perioden minimiert wird. Wie groß ist der Kostenunterschied durch diese Verwendung des Speichers im Vergleich zu ohne Speicher?
Hinweis: Der zweite Aufgabenteil ist schwiergier als der erste, da er an sich die Minimierung einer nicht-linearen Zielfunktion beinhaltet: \(\min\limits_x\max\limits_{t = 0,\ldots,5} |n_t|\). Durch eine zusätzliche Variable, nennen wir sie \(y\), läßt sich diese Optimierung aber in eine lineare transformieren: \(\min y\) mit der zusätzlichen Nebenbedingung \(-y \leq n_t \leq y\) für alle \(t = 0,\ldots,5\).
Abgabe: Hochladen eines IPython-Notebooks als ipynb-Datei in ILIAS
Lösung:
Konfiguration:
Zeitschritt: \(\Delta t = 1\) h
Zeitintervalle: \(T\) Stück, indiziert mit ihren Anfangszeitpunkten \(t = 0, 1, 2, ... , T-1\) in h
Leistung: in kW
Energie: in kWh
Kosten und Erlös: in EUR, gleiche Preise für Einspeisung und Abnahme
(Entscheidungs-)Variablen:
Leistungen in Stunde \(t\):
\(x_t\) … in den Speicher, Entscheidungsvariablen
\(d_t\) … Prosumerlast in den Haushalt, gegeben
\(n_t\) … aus dem Netz, ergibt sich aus \(x_t\) und \(n_t\)
Preise \(c_t\) in EUR/kWh, gegeben
Speicher: als verlustlos angenommen
Kapazitätsgrenzen: \(E_{\text{min}} = 0\) kWh und \(E_{\text{max}} = 6\) kWh
Anfangsstand: \(E_{\text{Anfang}} = 2.5\) kWh
Endstand: \(E_{\text{Ende}} = 2.5\) kWh
Leistungsgrenze für Laden und Entladen des Speichers: \(p_{\text{max}} = 2\) kW
Zielfunktionen:
(a) \(\min \sum_{t=0}^5 c_t n_t\) äquivalent zu \(\sum_{t=0}^5 c_t x_t\) da \(n_t = x_t + d_t\)
(b) \(\min\max\limits_{t = 0,\ldots,5} |n_t|\) äquivalent zu \(\min y\) und \(-y \leq n_t \leq y\)
Nebenbedingungen: mit \(E_t = E_{\text{Anfang}} + \sum_{\tau=0}^{t} x_\tau \Delta t\)
\(E_{\text{min}} \leq E_t \leq E_{\text{max}}\)
\(E_5 = E_{\text{Ende}}\)
\(-p_{\text{max}} \leq x_t \leq p_{\text{max}}\)
# Parameter:
T = 6 # Anzahl der Zeitintervalle
dt = 1
E_min = 0.0 # kWh
E_max = 6.0 # kWh
E_Anfang = 2.5 # kWh
E_Ende = 2.5 # kWh
p_max = 2.0 # kW
# Zeitreihen:
t = arange(0, T)
d = array([0.5, -1.0, -0.5, 1.5, 1.5, 0.5])
c = array([0.1, 0.08, 0.08, 0.12, 0.11, 0.12])
figure(figsize=(6, 5))
subplot(2,1,1)
plot(t, c, 'r.-')
xlabel("Zeit (h)")
ylabel('Preis (EUR/kWh)')
grid(True)
tight_layout()
subplot(2,1,2)
plot(t, d, '.-', label='Verbrauch')
xlabel("Zeit (h)")
ylabel('Leistung (kW)')
legend()
grid(True)
Kostenoptimierung:
# Nebenbedingungen:
M = tril(ones((T,T)))
A = vstack((M, -M))
b = array([E_max - E_Anfang]*T + [-E_min + E_Anfang]*T )
G = ones((1,T))*dt
h = array([E_Ende - E_Anfang])
res = linprog(c=c, A_ub=A, b_ub=b, A_eq=G, b_eq=h, bounds= (-p_max, p_max))
x = res.x
print(res)
con: array([8.23552115e-10])
fun: -0.1549999987239089
message: 'Optimization terminated successfully.'
nit: 6
slack: array([4.00000002e+00, 2.00000004e+00, 5.35733307e-08, 2.00000004e+00,
1.50000000e+00, 3.50000000e+00, 1.99999998e+00, 3.99999996e+00,
5.99999995e+00, 3.99999996e+00, 4.50000000e+00, 2.50000000e+00])
status: 0
success: True
x: array([-0.50000002, 1.99999998, 1.99999998, -1.99999998, 0.50000004,
-2. ])
n = x + d
C = dot(c, n)
D = dot(c, d)
print("Gesamtkosten Verbrauch = {:3.6f} EUR".format(D)) # https://pyformat.info/
print("Gesamtkosten optimiert = {:3.6f} EUR".format(C))
print("maximale Netzlast = {:3.6f} kW".format(max(abs(n))))
E = concatenate(([E_Anfang], E_Anfang + M@x*dt))
figure(figsize=(7, 7))
subplot(3,1,1)
plot(t, c, 'r.-', label='Preis')
hlines(mean(c), 0, T, linestyle='--', linewidth=1, label='Mittelwert')
xlabel("Zeit (h)")
ylabel('Preis (EUR/kWh)')
legend(bbox_to_anchor=(1.05, 1), loc=2)
grid(True)
tight_layout()
subplot(3,1,2)
plot(t, d, '.-', label='in den Haushalt')
plot(t, x, '.-', label='in den Speicher')
plot(t, n, '.-', label='vom Netz')
hlines(-p_max, 0, T, linestyle='--', linewidth=1, label='E_min')
hlines( p_max, 0, T, linestyle='--', linewidth=1, label='E_max')
xlabel("Zeit (h)")
ylabel('Leistung (kW)')
legend(bbox_to_anchor=(1.05, 1), loc=2)
grid(True)
subplot(3,1,3)
plot(arange(0, T + dt), E, '.-', label='Energie im Speicher')
hlines(E_min, 0, 6, linestyle='--', linewidth=1, label='E_min')
hlines(E_max, 0, 6, linestyle='--', linewidth=1, label='E_max')
plot(0, E_Anfang, 'x')
plot(T, E_Ende, 'x')
xlabel("Zeit (h)")
ylabel('Energie (kWh)')
legend(bbox_to_anchor=(1.05, 1), loc=2)
grid(True)
Gesamtkosten Verbrauch = 0.335000 EUR
Gesamtkosten optimiert = 0.180000 EUR
maximale Netzlast = 2.000000 kW
Netzoptimierung:
# Zielfunktion:
m = zeros(T+1)
m[T] = 1
# m[:T] = c; m[T] = 0.0 # Variante 1
# m[:T] = c; m[T] = 0.1 # Variante 2
# Nebenbedingungen:
bounds = [(-p_max, p_max)]*6 + [(0, None)]
# bounds = [(-p_max, p_max)]*6 + [(0, .5)] # Variante 1
# bounds = [(-p_max, p_max)]*6 + [(0, None)] # Variante 2
M = tril(ones((T,T)))
A1 = hstack( ( vstack((M, -M)), zeros((2*T,1)) ) )
A2 = hstack( ( -eye(T),-ones((T,1)) ) )
A3 = hstack( ( eye(T),-ones((T,1)) ) )
A = vstack( (A1, A2, A3) )
b1 = array([E_max - E_Anfang]*T + [-E_min + E_Anfang]*T )
b2 = concatenate( (d, -d) )
b = concatenate( (b1,b2) )
G = hstack( (ones((1,T))*dt, array([[0]])) )
h = array([E_Ende - E_Anfang])
res = linprog(c=m, A_ub=A, b_ub=b, A_eq=G, b_eq=h, bounds=bounds)
print(res)
x = res.x[:-1]
y = res.x[-1]
con: array([4.77430762e-10])
fun: 0.416666667876955
message: 'Optimization terminated successfully.'
nit: 6
slack: array([3.58333333e+00, 2.16666667e+00, 1.25000000e+00, 2.33333333e+00,
3.41666667e+00, 3.50000000e+00, 2.41666667e+00, 3.83333333e+00,
4.75000000e+00, 3.66666667e+00, 2.58333333e+00, 2.50000000e+00,
8.33333335e-01, 8.33333332e-01, 8.33333335e-01, 8.33333335e-01,
8.33333334e-01, 8.33333336e-01, 4.74684070e-10, 3.61962882e-09,
1.00340064e-09, 1.23707378e-09, 1.29069933e-09, 1.13674403e-10])
status: 0
success: True
x: array([-0.08333333, 1.41666666, 0.91666667, -1.08333333, -1.08333333,
-0.08333333, 0.41666667])
n = x + d
C = dot(c, n)
D = dot(c, d)
print("Gesamtkosten Verbrauch = {:3.6f} EUR".format(D)) # https://pyformat.info/
print("Gesamtkosten optimiert = {:3.6f} EUR".format(C))
print("maximale Netzlast = {:3.6f} kW".format(y))
E = concatenate(([E_Anfang], E_Anfang + M@x*dt))
figure(figsize=(7, 7))
subplot(3,1,1)
plot(t, c, 'r.-', label='Preis')
hlines(mean(c), 0, T, linestyle='--', linewidth=1, label='Mittelwert')
xlabel("Zeit (h)")
ylabel('Preis (EUR/kWh)')
legend(bbox_to_anchor=(1.05, 1), loc=2)
grid(True)
tight_layout()
subplot(3,1,2)
plot(t, d, '.-', label='in den Haushalt')
plot(t, x, '.-', label='in den Speicher')
plot(t, n, '.-', label='vom Netz')
hlines(-p_max, 0, T, linestyle='--', linewidth=1, label='E_min')
hlines( p_max, 0, T, linestyle='--', linewidth=1, label='E_max')
xlabel("Zeit (h)")
ylabel('Leistung (kW)')
legend(bbox_to_anchor=(1.05, 1), loc=2)
grid(True)
subplot(3,1,3)
plot(arange(0, T + dt), E, '.-', label='Energie im Speicher')
hlines(E_min, 0, 6, linestyle='--', linewidth=1, label='E_min')
hlines(E_max, 0, 6, linestyle='--', linewidth=1, label='E_max')
plot(0, E_Anfang, 'x')
plot(T, E_Ende, 'x')
xlabel("Zeit (h)")
ylabel('Energie (kWh)')
legend(bbox_to_anchor=(1.05, 1), loc=2)
grid(True)
Gesamtkosten Verbrauch = 0.335000 EUR
Gesamtkosten optimiert = 0.254167 EUR
maximale Netzlast = 0.416667 kW
Heimspeicherbewirtschaftung¶
Wir betrachten einen elektrischen Heimspeicher, der auf folgende Art in einem Haushalt verwendet wird:
Der Speicher “sitzt zwischen” dem Hausanschluss und dem Verbrauch des Haushalts: Die gesamte elektrische Energie des Energieversorgers fließt in den Speicher, und alle Verbräuche im Haushalt werden vollständig aus dem Speicher entnommen.
Der aggregierte Verbrauchsverlauf des Haushalts über einen Tag hinweg wird als bekannt vorausgesetzt.
Der Speicher hat einen Wirkungsgrad von 0.9, jeweils für das Laden und das Entladen.
Zu Tagesbeginn hat der Speicher einen Speicherstand von 5 kWh. Der minimale Speicherstand ist 0 kWh, der maximale 10 kWh.
Die Ladeleistung des Speichers beträgt maximal 15 kW.
In einer zeitlichen Auflösung von einer Stunde wird ein ganzer Tag betrachtet. Es ergeben sich somit
24 Stundenwerte für den Konsum des Haushalts, d. h. den Lastverlauf vom Energieversorger in den Speicher
25 Stundenwerte für den Speicherstand
24 Stundenwerte für den Verbrauch, d. h. den Lastverlauf vom Speicher weg zu den elektrischen Verbrauchern des Haushalts.
Wir verwenden folgende Einheiten:
Zeit: h
Leistung, Last: kW
Energie: kWh
Kosten: EUR
Aufgaben:
Laden Sie von der EXAA die Spot-Marktdaten für 2019 herunter. Wählen Sie einen Markt und einen Tag, und stellen Sie die 24-Stunden-Preise dazu grafisch dar. Die Preise sind in EUR/MWh gegeben.
Laden Sie von www.stromnetz.berlin das Standardlastprofil Haushalt 2019 herunter. Normieren Sie den 24-Stunden-Lastgang für Ihren gewählten Tag auf einen Tagesverbrauch von 13 kWh und stellen Sie ihn grafisch dar.
Erstellen Sie eine Skizze des Modells inkl. allen Variablen und Parametern.
Erstellen Sie ein lineares Programm (LP) für minimale Kosten über den gewählten Tag mit dem Konsum-Lastverlauf als Entscheidungsvariablen. Geben Sie die Zielfunktion und die Nebenbedingungen des LP an.
Lösen Sie das LP. Vergleichen Sie die minimalen Tageskosten mit jenen ohne Speicher. Stellen Sie den Konsum-Lastverlauf sowie den Speicherstand grafisch dar. Geben Sie die Speicherverluste an.
Welche Mängel hat das Modell, und wie kann es realisitischer gestaltet werden? Es genügt, wenn Sie Ihre Antworten in Worten beschreiben.
Abgabe: Hochladen eines IPython-Notebooks als ipynb-Datei in ILIAS.
Lösung:
# times vector:
times = arange(0, 24) # h, sampling interval = 1 h
# EXAA: dshistory2019.xls: Montag 23. September 2019, sheet "Price AT (EUR)", EUR/kWh
price = array([34.20, 34.01, 33.03, 33.04, 34.00, 34.44, 47.40, 50.40, 55.93, 53.10, 53.00, 51.95,
50.93, 50.98, 50.70, 49.95, 49.48, 52.96, 57.85, 60.95, 56.90, 50.94, 48.00, 43.50])/1000
# stromnetz berlin: standardlastprofil-haushalt-2019-09-23.xlsx, kWh
demand = array([64.777, 46.136, 40.266, 38.481, 38.972, 43.257, 71.628, 110.62, 122.383, 121.937, 118.812, 117.495,
129.66, 133.945, 116.714, 104.036, 95.331, 99.773, 122.071, 149.213, 153.386, 141.289, 127.651, 97.674])
# rescale to daily demand of 13 kWh
demand = demand/sum(demand)*13
# plot
figure(figsize=(5,6))
subplot(2,1,1)
plot(times, price, '.-r', label='price (EUR/kWh)')
xlabel('times (h)')
ylabel('price (EUR/kWh)')
title('Monday 23. September 2019, EXAA Price AT')
grid(True)
subplot(2,1,2)
plot(times, demand, '.-b', label='demand (kW)')
xlabel('times (h)')
ylabel('demand (kW)')
title('Monday 23. September 2019, EXAA Price AT')
grid(True)
tight_layout()
\(t\) … Zeit in h
\(dt\) … Zeitintervall = 1 h
\(x_t\) … Konsum in kW
\(d_t\) … Verbrauch in kW
\(S_t\) … Speicherstand in kWh
\(c_t\) … Preis in EUR/kWh
\(\eta_{\text{in}}\) … Wirkungsgrad des Ladens
\(\eta_{\text{out}}\) … Wirkungsgrad des Enladens
Es gilt:
LP:
# sampling interval:
dt = 1 # h
# decision variable bounds:
x_min = 0 # kW
x_max = 15 # kW
# efficiencies:
eta_in = 0.9
eta_out = 0.9
# storage:
S_min = 0 # kWh
S_max = 10 # kWh
S_0 = 5 # kWh
M = tril( eta_in*ones((24, 24)) )
A = vstack((-M, M))
b1 = ( S_0 - S_min)*ones((24, 1)) - reshape(cumsum(demand/eta_out)*dt, (-1,1))
b2 = (-S_0 + S_max)*ones((24, 1)) + reshape(cumsum(demand/eta_out)*dt, (-1,1))
b = vstack((b1, b2))
# print(A)
# print(b)
res = linprog(c=price,
A_ub=A, b_ub=b,
bounds=(x_min, x_max)
)
# print(res)
print("Minimale Kosten = {:.2f} EUR".format(res['fun']))
print("Benchmarkkosten = {:.2f} EUR".format(dot(price, demand)))
Minimale Kosten = 0.39 EUR
Benchmarkkosten = 0.65 EUR
consumption = res['x']
SOC = concatenate(([S_0], S_0 +
cumsum(consumption*dt)*eta_in -
cumsum(demand*dt)/eta_out))
storage loss = \((1 - \eta_{\text{in}})\sum_{t \in T} s^{\text{in}}_t \Delta t + (1/\eta_{\text{out}} - 1)\sum_{t \in T} s^{\text{out}}_t \Delta t\)
loss1 = (1 - eta_in)*sum(consumption)*dt + (1/eta_out - 1)*sum(demand)*dt
print("Speicherverluste = {:.5f} kWh".format(loss1))
# check:
loss2 = sum(consumption) + S_0 - sum(demand)
print("Speicherverluste = {:.5f} kWh".format(loss2))
Speicherverluste = 2.49383 kWh
Speicherverluste = 2.49383 kWh
# plot
figure(figsize=(5,6))
subplot(3,1,1)
plot(times, price, '.-r', label='price (EUR/kWh)')
xlabel('times (h)')
ylabel('price (EUR/kWh)')
title('Monday 23. September 2019, EXAA Price AT')
grid(True)
subplot(3,1,2)
plot(times, demand, '.-b', label='demand (kW)')
plot(times, consumption, '.-g', label='consumption (kW)')
xlabel('times (h)')
ylabel('power (kW)')
legend()
title('Monday 23. September 2019, EXAA Price AT')
grid(True)
subplot(3,1,3)
# SOC
plot(arange(25), SOC, '.-k')
hlines(S_min, xlim()[0], xlim()[1], linestyles='--')
hlines(S_max, xlim()[0], xlim()[1], linestyles='--')
xlabel('times (h)')
ylabel('SOC (kWh)')
title('Monday 23. September 2019, EXAA Price AT')
grid(True)
tight_layout()
Welche Mängel hat das Modell des Heimspeichers, und wie kann es realisitischer gestaltet werden?
direkter Konsum am Speicher vorbei ermöglichen
\(S_{24}\) fixieren
Unsicherheit des Verbrauchs einbauen
Transport- und Zuordnungsprobleme¶
Ein Unternehmen, das in verschiedenen Städten vier Brauereien betreibt, kann bei drei landwirtschaftlichen Genossenschaften den zur Produktion notwendigen Weizen beziehen. Die Brauerei B1 nimmt mindestens 30 t, die Brauereien B2 bis B4 nehmen genau 40, 20 bzw. 10 t Weizen von den Genossenschaften ab. Mit der Genossenschaft G1 besteht ein Abnahmevertrag über mindestens 35 t, wobei der Preis 5 GE/t beträgt (GE steht für Geldeinheiten, z. B. 1000 EUR). Die Genossenschaft G2 bietet maximal 50 t an; der Preis beträgt 4 GE/t. Sowohl bei G1 als auch bei G2 müssen die Weizenlieferungen selbst abgeholt werden. Dagegen bietet die Genossenschaft G3 maximal 30 t für 6 GE/t an, wobei die Anlieferung im Preis inbegriffen ist. Das Unternehmen möchte die Beschaffungskosten für den benötigten Weizen minimieren. Die Kosten \(C_{ij}\) für den Transport einer Tonne Weizen von Genossenschaft \(G_i\) zur Brauerei \(B_j\) können der Matrix \(C\) entnommen werden:
\[\begin{split}C = \begin{pmatrix}2 & 4 & 3 & 2 \\ 3 & 4 & 2 & 1 \\4 & 3 & 3 & 4 \end{pmatrix}.\end{split}\]Lösen Sie das entsprechende LP.
Eine Firma hat drei neue Maschinen verschiedener Typen gekauft. Es gibt vier mögliche Standorte, an denen jeweils maximal eine Maschine installiert werden kann. Einige dieser Standorte sind für bestimmte Maschinen aufgrund der Kosten des Materialtransport zu den Maschinen wünschenswerter als andere. Ziel ist es daher, eine Zuordnung der neuen Maschinen an die verfügbaren Standorte zu finden, die die Gesamtkosten des Materialtransports zu den Maschinen minimiert. Die Kosten in Euro pro Stunde für den Materialtransport für die jeweiligen Standorte sind in der Tabelle unten angeführt. Standort 2 ist nicht geeignet für Maschine 2, so dass für diesen Fall keine Kosten angegeben sind. Lösen Sie das entsprechende LP ohne die Ganzzahligkeit der Entscheidungsvariablen miteinzubeziehen. Überprüfen Sie stattdessen anschließend, ob die Lösung ganzzahlig ist.
Maschine
Standort 1
Standort 2
Standort 3
Standort 4
1
13
16
12
11
2
15
-
13
20
3
5
7
10
6
Links:
Abgabe: Hochladen eines IPython-Notebooks als ipynb-Datei in ILIAS.
Lösung der Aufgabe 1:
Quelle: Domschke: Übungen und Fallbeispiele zum Operations Research. 8. Auflage, 2015, Aufgabe 4.7
\(m_{ij}\) bezeichne die Menge in Tonnen von Genossenschaft \(i\) an Brauerei \(j\). Entscheidungsvektor \(x = (m_{11},...,m_{14},m_{21},...,m_{24},m_{31},...,m_{34})^T\)
# objective function coefficients:
c = np.array([8,9,7,6, 6,8,7,6, 6,6,6,6])
e4 = np.array([[1,1,1,1]])
z4 = np.array([[0,0,0,0]])
A = np.concatenate((
np.hstack((-e4, z4, z4)),
np.hstack(( z4, e4, z4)),
np.hstack(( z4, z4, e4)),
np.array([[-1,0,0,0,-1,0,0,0,-1,0,0,0,]])
), axis=0)
b = np.array([-35, 50, 30, -30])
G = np.array([[0,1,0,0, 0,1,0,0, 0,1,0,0],
[0,0,1,0, 0,0,1,0, 0,0,1,0],
[0,0,0,1, 0,0,0,1, 0,0,0,1]
])
h = np.array([40, 20, 10])
res = linprog(c=c, A_ub=A, b_ub=b, A_eq=G, b_eq=h, bounds=(0,None))
print("Minimale Kosten = {:.2f}".format(res['fun']))
x = np.round(res['x'], decimals=3)
m = np.reshape(x, (3,4))
m
Minimale Kosten = 645.00
array([[ 0., 5., 20., 10.],
[30., 5., 0., 0.],
[ 0., 30., 0., 0.]])
Lösung der Aufgabe 2:
Quelle: Hillier, Lieberman: Introduction to Operations Research. 10. Auflage, 2015, S. 348 ff.
# objective function coefficients:
M = 1000000
c = np.array([13,16,12,11, 15,M,13,20, 5,7,10,6])
e4 = np.array([[1,1,1,1]])
z4 = np.array([[0,0,0,0]])
G = np.concatenate((
np.hstack(( e4, z4, z4)),
np.hstack(( z4, e4, z4)),
np.hstack(( z4, z4, e4))
), axis=0)
h = np.array([1, 1, 1])
E4 = np.eye(4)
A = np.concatenate((E4, E4, E4), axis=1)
b = np.ones(4)
res = linprog(c=c, A_ub=A, b_ub=b, A_eq=G, b_eq=h, bounds=(0,None))
print("Minimale Kosten = {:.2f}".format(res['fun']))
x = np.round(res['x'], decimals=3)
z = np.reshape(x, (3,4))
z
Minimale Kosten = 29.00
array([[0., 0., 0., 1.],
[0., 0., 1., 0.],
[1., 0., 0., 0.]])
