Lineare gewöhnliche Differentialgleichungen 2. Ordnung - Übungen
Contents
Lineare gewöhnliche Differentialgleichungen 2. Ordnung - Übungen¶
%pylab inline
%config InlineBackend.figure_format = 'svg'
import sympy as sp
%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib
Aufgaben¶
Aufgabe LDG2-1: Lineare DGL 2. Ordnung¶
Lösen Sie die Differentialgelichung \(\ddot{y} + 3\dot{y} + 2y = 0\) mit den Anfangsbedingungen \(y(0)=2\) und \(\dot{y}(0)= -3\) von Hand und überprüfen Sie Ihr Ergebnis am Computer symbolisch.
Aufgabe LDG2-2: Lineare DGL 2. Ordnung¶
Bestimmen Sie die Lösungen folgender GDGL bzw. Anfangswertprobleme. Beschreiben Sie die Lösungen und deren Verhalten für \(x \rightarrow \infty\).
\(y''(x) + 5y'(x) - 6y(x) = 0\)
\(y''(x) - y(x) = 0\), \(y(0)=1\) und \(y'(0)= 0\)
Quelle: Farlow: An Introduction to Differential Equations and their Applications. Sec. 3.4., Example 1, p. 131f.
Aufgabe LDG2-3: Lineare DGL 2. Ordnung¶
Wir betrachten die GDGL \(y''(x) - 2y'(x) + y(x) = e^{3x}\).
Zeigen Sie, dass \(\frac{1}{4}e^{3x}\) eine partikuläre Lösung ist.
Bestimmen Sie die allgemeine Lösung.
Quelle: Bronson: Differential Equations. 4. Auflage, Aufgabe 8.23, S. 79.
Aufgabe LDG2-4: Lineare DGL 2. Ordnung¶
Bestimmen Sie die Lösungen folgender Anfangswertprobleme und beschreiben Sie die Lösungen und deren Verhalten für \(x \rightarrow \infty\)
\(y''(x) + 6y'(x) + 9y(x) =0\), \(y(0)=1\) und \(y'(0)= 2\)
\(y''(x) + 8y'(x) + 20y(x) =0\), \(y(0)=1\) und \(y'(0)= 6\)
Quelle: Dietmaier, p. 474, Aufgaben 12.9 b) und c)
Lösungen¶
Lösung LDG2-1: Lineare DGL 2. Ordnung¶
Siehe LDG2-1.jpg.
\(y(t) = e^{-t} + e^{-2t}\)
sp.init_printing()
t = sp.symbols('t')
y = sp.symbols('y', cls=sp.Function)
diffeq = sp.Eq(y(t).diff(t).diff(t) + 3*y(t).diff(t) + 2*y(t), 0)
diffeq
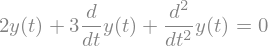
ys = sp.dsolve(diffeq, y(t))
ys

sp.init_printing(False)
Lösung LDG2-2: Lineare DGL 2. Ordnung¶
Siehe LDG2-2.jpg.
\(y(x) = c_1 e^{-6x} + c_2 e^{x}\)
\(y(x) = \cosh(x)\)
Lösung LDG2-3: Lineare DGL 2. Ordnung¶
Siehe LDG2-3.jpg.
durch Einsetzen
\(y(x) = c_1 e^x + c_2 xe^x + \frac{1}{4}e^{3x}\)
Lösung LDG2-4: Lineare DGL 2. Ordnung¶
Siehe LDG2-4.jpg.
\(y(x) = e^{-3x}(c_1 + c_2 x) = e^{-3x}(1 + 5x)\)
\(y(x) = e^{-4x}(c_1 \cos(2x) + c_2\sin(2x)) = e^{-4x}(\cos(2x) + 5\sin(2x))\)
x = linspace(0,3, 100)
y = exp(-3*x)*(1 + 5*x)
fig = figure()
fig.set_size_inches(6, 3)
plot(x, y)
xlabel('x')
ylabel('y')
grid(True)
x = linspace(0,3, 100)
y = exp(-4*x)*(cos(2*x) + 5*sin(2*x))
fig = figure()
fig.set_size_inches(6, 3)
plot(x, y)
xlabel('x')
ylabel('y')
grid(True)
print(min(y))
-0.0024990299146947434
Kurztestfragen¶
Bestimmen Sie die allgemeine Lösung der DGL \(\ddot{y}(t) + 5 \dot{y}(t) + 6y(t) = 0\).
Beschreiben Sie die allgemeine Lösungsstruktur von linearen inhomogenen GDGL 2. Ordnung mit konstanten Koeffizienten.
Bestimmen Sie die allgemeine Lösung der DGL \(\ddot{y}(t) + 4 \dot{y}(t) + 4y(t) = 0\).
Erläutern Sie die DGL \(m\ddot{y}(t) = -d\dot{y}(t) -ky(t)\) der gedämpften harmonischen Schwingung.
Was ist der Unterschied zwischen einem Anfangswertproblem und einer Differentialgleichung?
Was ist der Unterschied zwischen einer allgemeinen und einer speziellen/partikulären Lösung einer Differentialgleichung?
Ein Quader der Masse \(m=4\) kg bewegt sich auf einer reibungsfreien Unterlage. Der Quader ist über einen Dämpfer und eine Feder mit der Wand verbunden. Die Dämpfungskraft kann durch \(F_\text{d} = k\dot{x}\) mit \(k=4\) kg/s beschrieben werden, die Federkraft durch \(F_\text{f} =c x\) mit \(c=17\) kg/s\(^2\). Der Quader besitzt zu Beginn der Betrachtung die Geschwindigkeit \(4\) m/s und die Auslenkung \(0\) m. Zu diesem Zeitpunkt ist die Feder entspannt.
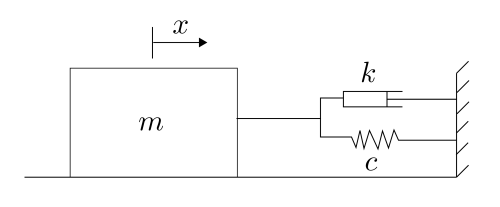
Formulieren Sie die Differentialgleichung, die die Position des Quaders beschreibt. Sollten Sie diesen Punkt nicht lösen können, können Sie mit \(\ddot{x}+8\dot{x}+20=0\) weiterrechnen.
Charakterisieren Sie die Differentialgleichung bezüglich Homogenität, Ordnung und Linearität.
Lösen Sie die charakteristische Gleichung und geben Sie die allgemeine Lösung der Differentialgleichung \(x(t)\) an.
Verwenden Sie die Anfangsbedingungen, um die partikuläre Lösung der DGL zu berechnen.
Skizzieren Sie qualitativ den Verlauf der Position des Quaders \(x(t)\).
Zeigen Sie, dass \(y(x) = \frac{1}{3} e^{3x}\) eine partikuläre Lösung der Differentialgleichung \(y''-8y' + 18y = e^{3x}\) ist.
