Lineare gewöhnliche Differentialgleichungen 1. Ordnung - Übungen
Contents
Lineare gewöhnliche Differentialgleichungen 1. Ordnung - Übungen¶
%pylab inline
%config InlineBackend.figure_format = 'svg'
from scipy.integrate import odeint
import sympy as sp
%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib
Aufgaben¶
Aufgabe LDG1-1: Menge an \(CO_2\) in einem Raum¶
Die Luft in einem Raum voller Menschen enthält im Volumenanteil 0,25% Kohlendioxid (\(CO_2\)). Eine Klimaanlage wird eingeschaltet und bläst mit einer Geschwindigkeit von 500 Kubikmeter pro Minute Frischluft in den Raum. Die frische Luft vermischt sich mit der verbrauchten Luft, und das Gemisch verlässt den Raum mit einer Geschwindigkeit von 500 Kubikmeter pro Minute. Die frische Luft enthält 0,01% \(CO_2\), und der Raum hat ein Volumen von 2500 Kubikmetern.
Bestimmen Sie die DGL, die das Volumen \(y(t)\) an \(CO_2\) im Raum zu jedem Zeitpunkt \(t\) erfüllt. Lösen Sie das Anfangswertproblem, und machen Sie einen Plot der Lösung in Python.
Das in 1. entwickelte Modell ignoriert das durch die Atmung der Personen im Raum erzeugte \(CO_2\). Nehmen wir an, dass die Menschen im Raum 0,08 Kubikmeter \(CO_2\) pro Minute produzieren. Berücksichtigen Sie in einer neuen DGL diese zusätzliche \(CO_2\)-Quelle. Lösen Sie das Anfangswertproblem, und machen Sie einen Plot der Lösung in Python zum Vergleich mit der Lösung in 1..
Quelle: Goldstein, Lay et al.: Calculus & Its Applications. 13th ed., p.546, Exercise 21
Aufgabe LDG1-2: Linearer Luftwiderstand¶
Eine Person mit einer Masse von 70 kg springt mit einem offenen Fallschirm ohne Anfangsgeschwindigkeit aus einer Höhe von 1000 m. Die Luftwiderstandskraft sei gleich \(140v(t)\) Newton, wobei \(v(t)\) die Geschwindigkeit der Person in Metern pro Sekunde bezeichnet.
Bestimmen Sie die DGL für \(v(t)\). Lösen Sie das Anfangswertproblem und erstellen Sie einen Plot der Lösung in Python.
Bestimmen Sie die Grenzgeschwindigkeit und graphisch die Zeit bis zum Bodenkontakt.
Quelle: Bronson, Schaum’s “Differential Equations”, 3rd edition, p.60, Exercise 7.12
Aufgabe LDG1-3: RL Schaltung¶
Die DGL, die die elektrische Stromstärke \(I(t)\) (A) zu einem Zeitpunkt \(t\) in einer RL-Schaltung beschreibt, ist gegeben durch
wobei \(R\) (\(\Omega\)) den Widerstand, \(L\) (H) die Induktivität und \(U\) (V) die Spannung ist. Eine gegebene Schaltung habe eine Spannung von 5 V, einen Widerstand von 50 \(\Omega\), eine Induktivität von 1 H sowie anfangs eine Stromstärke \(I(0)=0\). Berechnen Sie die Stromstärke \(I(t)\) für \(t\geq 0\), und erzeugen Sie einen Plot der Lösung in Python.
Quelle: Bronson, Schaum’s “Differential Equations”, 3rd edition, p.52, p.65, Exercise 7.19
Aufgabe LDG1-4: Lineare DGL 1. Ordnung mit variablen Koeffizienten¶
Lösen Sie die DGL
mit der Lösungsformel
für \(A(t) = \int a(t)\text{d}t\). Überprüfen Sie Ihr Ergebnis am Computer mittels SymPy.
Aufgabe LDG1-5: Newtonsches Abkuehlungsgesetz¶
Eine hungrige Studentin schaltet den Ofen ein und legt eine kalte Pizza aufs Blech, ohne den Ofen vorzuheizen. Sei \(T_P(t)\) die Temperatur der Pizza und \(T_O(t)\) die Ofentemperatur (°C) jeweils \(t\) Minuten, nachdem der Ofen angeschalten wurde. Nach dem Newtonschen Abkühlungsgesetz ist die Temperaturänderungsrate proportional zur Temperaturdifferenz von Pizza zu Ofen:
wobei \(k\) eine positive Konstante ist. Angenommen die Ofentemperatur ist für \(0\,\text{min} \leq t \leq 8\,\text{min}\) gegeben durch \(T_O(t)= 20 + 30t\), mit \(k= 0.1\,\text{min}^{-1}\) und einer anfänglichen Pizzatemperatur von 4°C.
Bestimmen Sie die Temperatur der Pizza in den ersten 8 Minuten.
Überprüfen Sie das Resultat in Python, und plotten Sie die Temperatur der Pizza über die ersten 8 Minuten.
Quelle: Lay p. 526f
Aufgabe LDG1-6: Solarthermie¶
Das Heizungssystem eines Gebäudes bestehe aus Solarkollektoren und einem Warmwasserspeicher. Der Warmwasserspeicher habe eine Zeitkonstante von \(\frac{1}{k} = 50\) Stunden, d. h. er kühlt ohne Wärmezufuhr nach dem Newtonschen Abkühlungsgesetz \(\dot{T}(t) = - k[T(t) - T_U(t)]\) aus, wobei \(T_U(t)\) die Umgebungstemperatur zur Stunde \(t\) ist. Der solare Eintrag führt pro Stunde zu einer Temperaturerhöhung um 2 °C im Speicher. Um 9 Uhr morgens (\(t=0\)) habe der Speicher eine Wassertemperatur von 30 °C und die Umgebungstemperatur sei den ganzen Tag über bei 20 °C.
Stellen Sie die Differentialgleichung inkl. Anfangsbedingung auf, die den Temperaturverlauf des Warmwasserspeichers bei Sonneneinstrahlung ab 9 Uhr beschreibt.
Lösen Sie dieses Anfangswertproblem.
Quelle: Farlow: An Introduction to Differential Equations and Their Applications. Section 2.5, Problem 14, p. 76.
Aufgabe LDG1-7: Elektroautobatterie¶
Das Elektroauto Think City verfügt über eine Zebra-Batterie (Natrium-Nickelchlorid) mit einer maximalen Lade- und Entladeleistung von \(P_{\text{max}} = 30\) kW und einer Kapazität von \(E_{\text{max}} = 20\) kWh. Ein elektrischer Widerstand in der Batterie wandelt elektrische Energie in Wärme um, die die Batterie während dem Laden und Entladen auf Betriebstemperatur hält. Dieser Widerstand und folglich auch die resultierenden thermischen Verluste hängen linear vom momentanen Ladezustand der Batterie ab, bei einer Verlustleistung von minimal \(I_{\text{min}} = 40\) W und maximal \(I_{\text{max}} = 120\) W. Die in der Batterie gespeicherte Energie kann demnach für \(E(t) > 0\) beschrieben werden durch:
Skizzieren Sie die thermischen Verluste in Abhängigkeit der gespeicherten Energie und erklären Sie die Differentialgleichung.
Lösen Sie das Anfangswertproblem \(E(0) = 10\) kWh bei einer konstanten Ladeleistung von \(P = 20\) kW. Wann ist die Batterie vollständig geladen?
Bei einer konstanten Entladeleistung von \(P = -10\) kW, wie hoch ist der Energieinhalt der Batterie nach einer Stunde, wenn die Batterie zu Beginn voll geladen war?
Aufgabe LDG1-8: Waermeuebertrager¶
Die beiden Fluidtemperaturen in einem Gleichstrom-Wärmeübertrager können durch folgendes Differentialgleichungssystem beschrieben werden.
Dabei beschreiben \(T_1, T_2\) (K) die Fluidtemperaturen, \(x\) (m) die Position im eindimensional beschriebenen Wärmetauscher, \(L\) (m) die Länge des Wärmetauschers und \(\text{NTU}_1, \text{NTU}_2 >0\) (-) die Übertragungsfähigkeit (Number of Transfer Units).
Einstromwärmetauscher: Es sei \(T_2\) konstant:
Lösen Sie die Differentialgleichung für \(T_1(x)\).
Welche Temperatur hat das Fluid 1 am Ende des Wärmetauschers bei einer Übertragungsfähigkeit \(\text{NTU}_1=2\), einer Wärmetauscherlänge von \(L=50\) cm und einer Anfangstemperatur von \(T_1(0)=4^{\circ}\text{C}\), wenn das andere Fluid eine konstante Temperatur von \(T_2=0^{\circ}\text{C}\) hat.
Skizzieren und interpretieren Sie die Lösung.
Gleichstromwärmetauscher: Führen Sie die Variable \(\theta = T_1-T_2\) ein.
Zeigen Sie, dass \(\theta\) die folgende Differentialgleichung efüllt:
\[\frac{d\theta(x)}{dx} = -\frac{\text{NTU}_1+\text{NTU}_2}{L}\theta(x)\]Lösen Sie damit das Anfangswertproblem \(T_1(0)=23^{\circ}\text{C}, T_2(0)=12^{\circ}\text{C}\).
Skizzieren Sie die Lösung und interpretieren Sie \(\theta(x)\).
Aufgabe LDG1-9: Newtonschen Abkuehlungsgesetz¶
Ein Körper mit einer unbekannten Temperatur wird in einen Raum mit konstanter Umgebungstemperatur von 30° C platziert. Nach 10 Minuten ist die Temperatur des Körpers 0° C und nach 20 Minuten ist sie 15° C. Bestimmen Sie die unbekannte Anfangstemperatur.
Hinweis: Newtonschen Abkühlungsgesetz \(\dot{T}(t) = - k[T(t) - T_U]\)
Quelle: Bronson: Schaum’s “Differential Equations”, Aufgabe 7.10, S. 59
Aufgabe LDG1-10: Mischung¶
Ein Tank enthält ursprünglich 200 Liter reines Wasser. Eine Salzlösung mit 1 kg Salz pro 4 Liter Wasser wird bei einer Rate von 12 Liter pro Minute in den Tank eingebracht. Salz und Wasser durchmischen sich perfekt, und 12 Liter der Mischung fließen pro Minute wiederum aus dem Tank heraus.
Stellen Sie die Differentialgleichung auf, die die Menge (in kg) an Salz im Tank über die Zeit hinweg beschreibt.
Lösen Sie diese Differentialgleichung.
Bestimmen Sie, falls vorhanden, den steady state.
Skizzieren Sie die Lösung.
Quelle: Farlow: Introduction to Differential Equations. Example 1, p. 61f.
Lösungen¶
Lösung LDG1-1: Menge an \(CO_2\) in einem Raum¶
Siehe LDG1-1.jpg.
\(\dot{y} = 0.05 - 0.2y, y(0) = 6.25\)
\(\dot{y} = 0.13 - 0.2y, y(0) = 6.25\)
t = linspace(0, 60)
y0 = 0.25/100*2500
print("y0 =", y0)
if True: # numerisch
def my_f1(y, t):
return 0.05 - 0.2*y
def my_f2(y, t):
return 0.13 - 0.2*y
y1 = odeint(my_f1, y0, t)
y2 = odeint(my_f2, y0, t)
else: # analytisch
y1 = 0.25 + 6.0*exp(-0.2*t)
y2 = 0.65 + 5.6*exp(-0.2*t)
figure(figsize=(5,3))
plot(t, y1, 'b', linewidth=2, label='ohne Menschen')
plot(t, y2, 'r', linewidth=2, label='mit Menschen')
ylabel('CO2 (m$^3$)')
xlabel('t (Minuten)')
legend()
grid(True)
y0 = 6.25
sp.init_printing(use_unicode=True)
t = sp.symbols('t')
y = sp.symbols('y', cls=sp.Function)
diffeq = sp.Eq(y(t).diff(t) + 0.2*y(t), 0.05)
diffeq
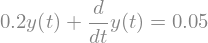
sp.dsolve(diffeq, y(t))

diffeq = sp.Eq(y(t).diff(t) + 0.2*y(t), 0.13)
diffeq
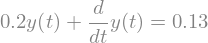
sp.dsolve(diffeq, y(t))

sp.init_printing(False)
Lösung LDG1-2: Linearer Luftwiderstand¶
Siehe LDG1-2.jpg.
m = 70 # kg
g = 9.81 # m/s^2
r = 140 # kg/s
v_limit = -m/r*g
print(v_limit, "m/s =", v_limit*3.6, "km/h")
t = linspace(0, 10)
v = -m/r*g*(1 - exp(-r/m*t))
-4.905 m/s = -17.658 km/h
figure(figsize=(5,3))
plot(t, v)
plot(t, v_limit*ones(shape(t)))
xlabel('t in Seconden')
ylabel('v in m/s')
grid(True)
t = linspace(0, 60*4)
#t = linspace(18, 20)
x = 1000 + (m/r)**2*g*(1 - exp(-r/m*t)) - m/r*g*t
figure(figsize=(5,3))
plot(t, x)
xlabel('t in seconds')
ylabel('x in m')
grid(True)
Lösung LDG1-3: RL Schaltung¶
Siehe LDG1-3.jpg.
t = linspace(0, 0.5)
I = 1/10*(1 - exp(-50*t))
figure(figsize=(5,3))
plot(t, I)
xlabel('t')
ylabel('I')
grid(True)
Lösung LDG1-4: Lineare DGL 1. Ordnung mit variablen Koeffizienten¶
Siehe LDG1-4.jpg.
sp.init_printing(use_unicode=True)
t = sp.symbols('t')
y = sp.symbols('y', cls=sp.Function)
diffeq = sp.Eq(y(t).diff(t) + t*y(t), 4*t)
diffeq
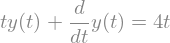
sp.dsolve(diffeq, y(t))

sp.init_printing(False)
Lösung LDG1-5: Newtonsches Abkuehlungsgesetz¶
Siehe LDG1-5.jpg.
sp.init_printing(use_unicode=True)
diffeq = sp.Eq(y(t).diff(t), -y(t)/10 + 2 + 3*t)
diffeq
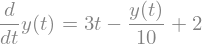
sp.dsolve(diffeq, y(t))

sp.init_printing(False)
t = linspace(0,8)
figure(figsize=(5,3))
plot(t, 284*exp(-0.1*t) - 280 + 30*t, label='Pizza')
plot(t, 20 + 30*t, label='Ofen')
legend()
xlabel('t in Minuten')
ylabel('T in Celsius')
grid(True)
Lösung LDG1-6: Solarthermie¶
Siehe LDG1-6.jpg.
\(\dot{T}(t) = - \frac{1}{50}[T(t) - 20] + 2\)
Siehe Code
t = linspace(0,12)
T0 = 30
TU = 20
a = 1/50
b = 2 + TU*a
T = T0*exp(-a*t) + b/a*(1 - exp(-a*t))
# T = 120 - 90*exp(-t/50)
figure(figsize=(5,3))
plot(t + 9, T)
grid(True)
Lösung LDG1-7: Elektroautobatterie¶
Siehe LDG1-7.jpg.
Emax = 20 #kWh,
Imax = 120*10**-3 #kW,
Imin = 80*10**-3 #kW
E = linspace(0,Emax)
Ploss = -Imax + (Imax - Imin)*E/Emax
figure(figsize=(5,3))
plot(E, Ploss, linewidth=2)
xlabel('E (kWh)')
ylabel('$P_{loss} (kW)$')
ylim(-Imax - 0.01, -0.06)
grid(True)
sp.init_printing(use_unicode=True)
Imax, Imin, Emax, P, t = sp.symbols('Imax Imin Emax P t')
E = sp.symbols('E', cls=sp.Function)
diffeq = sp.Eq(E(t).diff(t), -Imax +(Imax-Imin)/Emax*E(t)+P)
diffeq
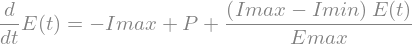
sp.dsolve(diffeq, E(t))

sp.init_printing(False)
Umformulierung mittels \(c=e^{C_1}\):
P = 20 #kW,
E0 = 10 #kWh
Emax = 20 #kWh,
Imax = 120*10** - 3 #kW,
Imin= 80*10** - 3 #kW
c = E0-Emax*(Imax-P)/(Imax-Imin)
c
9950.0
t = log((Emax - (Emax*(Imax-P)/(Imax - Imin)))/c)*Emax/(Imax - Imin)
t #min
0.5022602130027453
t = linspace(0,0.5)
E = c*exp((Imax - Imin)/Emax*t) + Emax*(Imax - P)/(Imax - Imin)
dotE = -Imax + P + (Imax - Imin)*E/Emax
#print(dotE)
figure(figsize=(5,3))
plot(t, E, linewidth = 2)
xlabel('t (hrs)')
ylabel('E (kWh)')
grid(True)
P = -10 #kW
E0 = Emax
c = E0-Emax*(Imax-P)/(Imax-Imin)
c
-5040.0
t1 =1
E = c*exp((Imax-Imin)/Emax*t1)+Emax*(Imax-P)/(Imax-Imin)
E
9.90991327663869
t = linspace(0,1.8)
E = c*exp((Imax-Imin)/Emax*t)+Emax*(Imax-P)/(Imax-Imin)
dotE = -Imax + P + (Imax - Imin)*E/Emax
#print(dotE)
figure(figsize=(5,3))
plot(t, E, linewidth=2)
xlabel('t (hrs)')
ylabel('E (kWh)')
grid(True)
Lösung LDG1-8: Wärmeübertrager¶
Siehe LDG1-8.jpg.
\(x\) … Position im Wärmeübertrager
\(T_1(x)\) … Temperatur warmes Fluid
\(T_{1in}=T_1(0)\) … Temperatur warmes Fluid vor dem Wärmeübertrager
\(T_{1out}=T_1(L)\) … Temperatur warmes Fluid nach dem Wärmeübertrager
\(T_2(x)\) … Temperatur kaltes Fluid
\(T_{2in}=T_2(0)\) … Temperatur kaltes Fluid vor dem Wärmeübertrager
\(T_{2out}=T_2(L)\) … Temperatur kaltes Fluid nach dem Wärmeübertrager
# Einstrom numerische Lösung:
L = 0.5;
N1 = 2;
T1_in = 4;
T2 = 0;
def dT1(T1,x):
return -N1/L*(T1-T2)
x1 = linspace(0, L, 100);
T1 = odeint(dT1, T1_in, x1);
figure(figsize=(5,3));
plot(x1, T1);
plot(x1,x1*T2);
legend(['$T_1$','$T_2$']);
ylim([-1,5]);
xlabel('x')
ylabel('Temperatur')
grid(True)
print('Temperatur am Ende des Wärmeübertragers: ',T1[-1])
Temperatur am Ende des Wärmeübertragers: [0.54134112]
4*exp(-2)
0.5413411329464508
# # Einstrom analytische Lösung:
x, N1, L, T2 = sp.symbols('x N1 L T2')
T1 = sp.symbols('T', cls=sp.Function)
equ = sp.Eq(T1(x).diff(x), -N1/L*(T1(x)-T2))
T1_fun = sp.dsolve(equ, T1(x))
sp.init_printing(use_unicode=True)
T1_fun

# Gleichstrom analytische Lösung:
T1_in = 23 # +273.15;#K
T2_in = 12 # +273.15;#K
x, N1, N2, L, theta = sp.symbols('x N1 N2 L theta')
theta = sp.symbols('theta', cls=sp.Function)
equ = sp.Eq(theta(x).diff(x), -(N1+N2)/L*(theta(x)))
T1_fun = sp.dsolve(equ, theta(x))
print("Analytische Lösung: ")
T1_fun
Analytische Lösung:

print('Anfangswerte liefern C1 = T_1(0) - T_2(0) =', T1_in - T2_in)
Anfangswerte liefern C1 = T_1(0) - T_2(0) = 11
# Gleichstrom numerische Lösung:
L = 1 #m
T0 = [T1_in, T2_in];
N1 = 1.5;
N2 = 0.5;
def dT(T, x1):
dotT0= -N1/L*(T[0]-T[1])
dotT1= -N2/L*(T[1]-T[0])
return [dotT0, dotT1]
x = linspace(0, L, 100);
T = odeint(dT, T0, x)
theta0 = T0[0] - T0[1];
theta = (theta0)*np.exp(-x*(N1+N2)/L);
figure(figsize=(5,3))
plot(x, T[:,0], x, T[:,1])
plot(x, theta)
legend(['$T_1$','$T_2$',"$T_1-T_2$"])
xlabel('x')
ylabel('Temperatur')
grid(True)
Lösung LDG1-9: Newtonschen Abkuehlungsgesetz¶
Siehe LDG1-9.jpg.
\(\dot{T} = -k(T - 30)\), Anfangstemperatur \(T(0)=-30\) °C
Lösung LDG1-10: Mischung¶
Siehe LDG1-10.jpg.
\(\dot{Q} = \frac{1}{4}12 - \frac{Q}{200}12\)
\(Q(t) = 50(1 - e^{-3t/50})\)
\(50\)
siehe Code
t = linspace(0, 120)
Q = 50*(1 - exp(-3*t/50))
figure(figsize=(5,3))
plot(t, Q)
xlabel('Zeit (Minuten)')
ylabel('Menge (kg)')
grid(True)
Kurztestfragen¶
Interpretieren Sie die Lösungsformel \(y(t)= y(0)e^{-at} + \frac{b}{a}\left( 1 - e^{-at} \right)\) für lineare GDGL erster Ordnung \(\dot{y} + ay = b.\)
Welchen steady state hat die DGL \(L\dot{I} + RI = U\)? Begründen Sie Ihre Antwort.
Erläutern Sie Newtons Abkühlgesetz \(\dot{T} = -\lambda (T - T_A)\).
Interpretieren Sie die allgemeine Lösung \(T(t) = \left( T(0)- T_A \right) e^{-\lambda t} + T_A\) von Newtons Abkühlgesetz.
Interpretieren Sie die Lösungsformel \(y(t)= \frac{b}{a} + \left(y(0)- \frac{b}{a}\right)e^{-at}\) für lineare Differentialgleichungen erster Ordnung \(\dot{y} + ay = b.\)
Eine Kugel der Masse \(1\) kg wird in einer zähen Flüssigkeit aus der Ruhe losgelassen. Auf die Kugel wirken während der Abwärtsbewegung in der Flüssigkeit eine Gewichtskraft, eine Auftriebskraft und eine Reibungskraft.
Skizzieren Sie die Kugel mit den an ihr angreifenden Kräften.
Die Auftriebskraft betrage konstant \(4\) N. Die Reibungskraft kann mit \(k=6\) kg/s anhand der Gleichung \(F_\mathrm{R}=k v\) beschrieben werden. Formulieren Sie die Differentialgleichung, die die Änderung der Geschwindigkeit der Kugel beschreibt.
Charakterisieren Sie die Differentialgleichung bezüglich Homogenität, Ordnung und Linearität.
Lösen Sie die Differentialgleichung.
Skizzieren Sie qualitativ den Verlauf der Geschwindigkeit der Kugel.
Zeigen Sie, dass das Differential, welches der Differentialgleichung \(\dot{y}+ay=b\) entspricht, für alle \(a\neq 0\) inexakt ist.
Welchen Steady-State besitzt die Differentialgleichung \(17\dot{y} + 34y = 68\)?
Erläutern Sie Newton’s Abkühlungsgesetz \(\dot{T}=-\lambda (T - T_\text{Umgebung})\).
Programmierprojekte¶
Modelle fuer die globale Durchschnittstemperatur der Erde¶
Wir können ein einfaches Modell der Temperatur auf der Erde machen, indem wir annehmen, dass die Erde Sonneneinstrahlung aufnimmt aber einen Teil davon wieder zurück in den Weltraum strahlt. Die globale Durchschnittstemperatur \(T\) kann dann durch folgende Energiebilanzgleichung modelliert werden:
Der erste Term auf der rechten Seite ist die von der Erde und ihrer Atmosphäre absorbierten Wärme. Der zweite Term ist die Wärme, die von der Erde ausgestrahlt wird, wenn man sie als schwarzen Körper modelliert.
\(T\) (K) ist die Durchschnittstemperatur in der Erdphotosphäre (obere Atmosphäre, wo die Energiebilanz in diesem Modell aufgestellt wird) in Kelvin.
\(t\) (a) ist die Zeit in Jahren.
\(R\) (Wa/(m\(^2\)K)) ist die gemittelte Wärmekapazität des Erde-Atmosphäre-Systems.
\(Q\) (W/m\(^2\)) ist der jährliche globale Mittelwert der einfallenden Sonnenstrahlung pro Quadratmeter Erdoberfläche.
\(\alpha\) (dimensionslos) ist die planetare Albedo (Reflektivität).
\(\sigma\) (W/(m\(^2\)K\(^4\))) ist die Stefan-Boltzmann-Konstante.
Die Parameter haben folgende Zahlenwerte:
\(R = 2.912\)
\(Q = 342\)
\(\alpha = 0.30\)
\(\sigma = 5.67\times 10^{-8}\)
Aufgaben:
Verwenden Sie für die angegebenen Parameterwerte den Python-Befehl
odeint, um numerische Lösungen der GDGL für unterschiedliche Anfangsbedingungen zu berechnen und zu plotten. Was beobachten Sie?Bestimmen Sie die steady-state Temperatur \(T^*\) der GDGL.
Die Erdatmosphäre (und der Treibhauseffekt) kann in das Modell durch Einbeziehung eines Emissionsfaktors \(\epsilon\) integriert werden:
\[R\frac{\text{d}T}{\text{d}t} = Q(1 - \alpha) - \epsilon\sigma T^4.\]Der Wert \(\epsilon = 1\) ergibt eine völlig transparente Atmosphäre. Welcher Wert von \(\epsilon\) ergibt für die angegebenen Werte der anderen Parameter eine Gleichgewichts-Globalmitteltemperatur von \(T^*\) = 288.4 K = 15.25 °C?
Wir modellieren nun die Abstrahlung der Erde statt über die Schwarzkörperstrahlung über einen linearen Term der Form \(A + BT\), mit B eine positive Konstante, und erhalten damit die folgende Energiebilanzgleichung:
In diesem Modell ist die globale durchschnittliche Oberflächentemperatur \(T\) in °C angegeben. Die Werte der Parameter \(R\), \(Q\) und \(\alpha\) sind von dieser Maßstabsänderung nicht betroffen.
Aufgaben:
Erläutern Sie die Anforderung, dass \(B > 0\) ist, und warum die Werte der Parameter \(R\), \(Q\) und \(\alpha\) von der Maßstabsänderung nicht betroffen sind.
Bestimmen Sie die allgemeine Lösung der linearen GDLG analytisch, d. h. als Formel. Plotten und diskutieren Sie diese anschließend.
Aktuelle Schätzungen für die Parameter \(A\) und \(B\) stammen aus Satellitenmessungen: \(A\) = 202 W/m\(^2\) und \(B\) = 1.90 W/(m\(^2\) C). Berechnen Sie daraus die mittlere Oberflächentemperatur \(T^*\) der Erde im Gleichgewicht, d. h. im steady-state. Wiederholen Sie die Berechnung für die folgenden Daten von 1979 für die nördliche Hemisphäre: \(A\) = 203,3 W/m\(^2\) und \(B\) = 2.09 W/(m\(^2\)C).
Abgabe: Hochladen eines Ipython-Notebook als ipynb-Datei und aller evtl. zusätzlichen (Daten-)Files in ILIAS.
Lösung:
Quellen:
Climate Modeling in Differential Equations. James Walsh, Dept. of Mathematics, Oberlin College. The UMAP Journal 36 (4) (2015).
Hans Kaper und Hans Engler: Mathematics and Climate. 2013, Google Books
# Parameter:
R = 2.912 # W a/(m^2 K)
Q = 342.0 # W/m^2
alpha = 0.30 #
sigma = 5.67e-8 # W/(m^2 K^4)
# Definition der Richtungsfeldfunktion:
def fun(T, t):
return (Q*(1 - alpha) - sigma*T**4)/R
# A sequence of time points for which to solve for T.
# The initial value point should be the first element of this sequence.
t = linspace(0, 1e1, num=100)
# The initial value:
T0_1 = 200.0 # K
T0_2 = 300.0 # K
# Solve numerically with odeint:
T_1 = odeint(fun, T0_1, t)
T_2 = odeint(fun, T0_2, t)
# steaty-state Temperatur:
Ts = (Q*(1 - alpha)/sigma)**0.25
print("steaty-state Temperatur = {:.2f} K = {:.2f} °C".format(Ts, Ts - 273.15))
figure(figsize=(6,4))
plot(t, T_1, '.-', label='T_1 (K)')
plot(t, T_2, '.-', label='T_2 (K)')
hlines(Ts, min(t), max(t), linestyle='--', label='steady-state')
xlabel('Zeit (a)')
ylabel('Temperatur (K)')
legend()
grid(True)
steaty-state Temperatur = 254.91 K = -18.24 °C
# Emissionsfaktor:
Tn = 288.4 # K
eps = Q*(1 - alpha)/(sigma*Tn**4)
print("Emissionsfaktor = {:.2f}".format(eps))
Emissionsfaktor = 0.61
Nach Umformen von
zu
vergleichen wir mit der allg. Form
die die Lösung
hat. So erhalten wir:
Die steady-state Temperatur ist:
A_1 = 202.0 # W/m^2
B_1 = 1.90 # W/(m^2 C)
A_2 = 203.3 # W/m^2
B_2 = 2.09 # W/(m^2 C)
t = linspace(0, 20, num=100)
T0 = 0.0 # °C
T_1 = (T0 - (Q*(1 - alpha) - A_1)/B_1)*exp(-B_1*t/R) + (Q*(1 - alpha) - A_1)/B_1
T_2 = (T0 - (Q*(1 - alpha) - A_2)/B_2)*exp(-B_2*t/R) + (Q*(1 - alpha) - A_2)/B_2
figure(figsize=(6,4))
plot(t, T_1, '.-', label='T_1 (K)')
plot(t, T_2, '.-', label='T_2 (K)')
xlabel('Zeit (a)')
ylabel('Temperatur (°C)')
legend()
grid(True)
print("steady-state 1 = {:.2f} °C".format((Q*(1 - alpha) - A_1)/B_1))
print("steady-state 2 = {:.2f} °C".format((Q*(1 - alpha) - A_2)/B_2))
steady-state 1 = 19.68 °C
steady-state 2 = 17.27 °C
Thermisches Demand Side Management¶
Sie duschen um 16:30 Uhr für eine halbe Stunde. Die mittlere Temperatur des Wassers in Ihrem 150 Liter Warmwasserboiler beträgt danach um 17 Uhr noch 20 °C. Nach 24 Stunden, d. h. um 17 Uhr am kommenden Tag, werden Sie wieder duschen. Die mittlere Wassertemperatur soll dann mindestens 50 °C betragen. Die stündlichen Arbeitspreise Ihres Stromlieferanten haben für die kommenden 24 Stunden folgende Werte in Cent/kWh: 12, 13, 15, 14, 15, 13, 13, 12, 12, 11, 9.95, 10, 11, 13, 12, 12, 11, 13, 15, 12, 11, 10, 11, 12. Die Umgebungstemperatur des Boilers beträgt konstant 15 °C.
Wir modellieren den Verlauf der mittlere Wassertemperatur mit folgender Differentialgleichung:
Größen:
\(t\) …. Zeit in Stunden
\(T_{\text{W}}(t)\) … mittlere Temperatur des Wassers in °C
\(P(t)\) … elektrische Heizleistung in kW
Parameter:
spezifische Wäremkapazität von Wasser \(c = 4.184\) kJ/(kg K)
Der 150 Liter Warmwasserboiler hat eine Masse von \(m = 150\) kg.
Wärmeübergangskoeffizient \(U\) mal Oberfläche \(A\): \(k = UA = 1.1972\) W/K
konstante Umgebungstemperatur \(T_{\text{U}} = 15\) °C
Anfangstempertatur des Wassers \(T_{\text{W,A}} = 20\) °C
gewünschte Endtemperatur des Wassers \(T_{\text{W,E}} = 50\) °C
maximale Temperatur des Wassers \(T_{\text{W, max.}} = 70\) °C
Aufgaben:
Erläutern Sie die einzelnen Terme der DGL und deren Zusammenhang.
Zeigen Sie, ausgehend von der Differentialgleichung für \(T_{\text{W}}(t)\), dass der Energieinhalt des Boilerwassers im Vergleich zur Umgebungstemperatur \(E(t):=cm\left[ T_{\text{W}}(t) - T_{\text{U}} \right]\) die Differentialgleichung \(\dot{E}(t) + \lambda E(t) = P(t)\) mit \(\lambda = \frac{k}{cm}\) erfüllt.
Wir suchen die kostenoptimalen Heizleistungen \(P_k\) in kW für \(k=0,\ldots,23\). Dies sind 24 für jeweils \(\Delta t = 1\) Stunde konstante Heizleistungen, mit denen Sie den Boiler bis zur nächsten Dusche steuern.
Sei \(E_n := E(n\Delta t)\) für \(n=0,\ldots,24\). Zeigen Sie, dass für \(n\geq1\) folgende Formel gilt:
\[E_n = e^{-\lambda n\Delta t} E_0 + \sum_{k=0}^{n-1} P_k \frac{1 - e^{-\lambda \Delta t}}{\lambda} e^{- \lambda (n - (k+1))\Delta t}.\]Lösen Sie das Kostenminimierungsproblem über die 24 Stunden bis zur nächsten Dusche unter den Nebenbedingungen, dass
die Endtemperatur \(T_W (n\Delta t)\) des Wassers mindestens \(T_{\text{W,E}} = 50\) °C beträgt.
die maximale Temperatur des Wassers den Grenzwert \(T_{\text{W, max.}} = 70\) °C nicht überschreitet.
\(0 \leq P_k \leq 2.2\) kW eingehalten wird.
Stellen Sie das Ergebnis grafisch dar und interpretieren Sie es in Worten.
Diskutieren Sie mit Ihrem Code mindestens drei Variationen der Situation, z. B. andere Parameterwerte oder andere Preise.
Abgabe: Hochladen eines IPython-Notebooks als ipynb-Datei in ILIAS.
Literatur: Wer mehr über das Thema thermisches Demand Side Management wissen möchte, kann z. B. mit folgenden Publikationen starten:
Peter Kepplinger, Gerhard Huber, Peter Amann, Klaus Rheinberger, Jörg Petrasch: Active Demand Side Management with Domestic Hot Water Heaters Using Binary Integer Programming. e-nova 2013 Nachhaltige Gebäude - Versorgung - Bewertung - Integration, Pinkafeld, Austria, 11/2013.
Peter Kepplinger, Gerhard Huber, Jörg Petrasch: Autonomous optimal control for demand side management with resistive domestic hot water heaters using linear optimization. Energy and Buildings, Volume 100, 2015, Pages 50-55, ISSN 0378-7788, https://doi.org/10.1016/j.enbuild.2014.12.016
Lösung:
# given parameters:
dt = 1 # time step (h)
c = 4.184/3600 # kWh/(kg K), 4.184 kJ/(kg K)
m = 150 # kg
k = 1.1972/1000 # kW/K, 1.1972 W/K
T_U = 15 # °C
T_WA = 20 # °C
T_WE = 50 # °C
T_Wmax = 70 # °C
# derived parameters:
lmbd = k/(c*m) # lambda
f = (1 - exp(-lmbd*dt))/lmbd
E_WA = c*m*(T_WA - T_U)
E_WE = c*m*(T_WE - T_U)
E_Wmax = c*m*(T_Wmax - T_U)
print("f = {:0.4f}".format(f))
f = 0.9966
# times/hours (h) after last shower:
times = arange(0, 24, dt) # 24 time periods
times_plot = arange(0, 25, dt) # 25 time points
times_plot_xticks = concatenate( (arange(17, 24), arange(0, 18)) ) # time on clock
# hourly prices (Cent/kWh) after last shower:
prices = array([ 12, 13, 15, 14, 15, 13, 13,
12, 12, 11, 9.95, 10, 11, 13, 12, 12, 11, 13, 15, 12, 11, 10, 11, 12 ])
# prices = ones_like(times)
figure(figsize=(8,5))
step(times_plot, append(prices, prices[-1]), '-k', where='post')
xticks(ticks=times_plot, labels=times_plot_xticks)
xlabel('time (h)')
ylabel('price (EUR/kWh)')
grid(True)
Lösung mit linprog:
from scipy.optimize import linprog
A1 = array([ [-f*exp( -lmbd*(24 - (k + 1))*dt ) for k in times] ])
b1 = array([ -E_WE + exp(-lmbd*24*dt)*E_WA ])
A2 = zeros( (24, 24) )
for t in times + dt:
for s in arange(0, t, dt):
A2[t - dt, s] = f*exp( -lmbd*(t - (s + 1))*dt )
b2 = array([ E_Wmax - exp(-lmbd*dt*t)*E_WA for t in times + dt ])
A = vstack((A1, A2))
b = concatenate((b1, b2))
res = linprog(c=prices*dt,
A_ub=A, b_ub=b,
bounds=(0, 2.2)
)
# print(res)
print("optimal costs = {:.2f} Cent".format(res['fun']))
optimal costs = 56.89 Cent
powers_sol = res['x']
E_W_sol = concatenate( ([E_WA], zeros_like(times)) )
for t in times:
E_W_sol[t + 1] = E_W_sol[t]*exp(-lmbd*dt) + powers_sol[t]*f
T_W_sol = E_W_sol/(c*m) + T_U
figure(figsize=(8,9))
subplot(3,1,1)
step(times_plot, append(prices, prices[-1]), '-k', where='post')
xticks(ticks=times_plot, labels=times_plot_xticks)
xlabel('time (h)')
ylabel('price (EUR/kWh))')
# xlim(-1, 25)
grid(True)
subplot(3,1,2)
step(times_plot, append(powers_sol, powers_sol[-1]), '-r', where='post')
xticks(ticks=times_plot, labels=times_plot_xticks)
xlabel('time (h)')
ylabel('power (kW)')
# xlim(-1, 25)
grid(True)
subplot(3,1,3)
plot(times_plot, T_W_sol, '.-b')
xticks(ticks=times_plot, labels=times_plot_xticks)
xlabel('time (h)')
ylabel('temperature (°C)')
xlim(-1, 25)
grid(True)
tight_layout()
