Arbeitsintegrale - Übungen
Contents
Arbeitsintegrale - Übungen¶
%pylab inline
%config InlineBackend.figure_format = 'svg'
Populating the interactive namespace from numpy and matplotlib
Aufgaben¶
Aufgabe AI1: Weg(un)abhängige Vefktorfelder bzw. (in)exakte Differentiale¶
Gegeben ist das Differential \(\delta f = y \,\text{d}x - x \,\text{d}y\).
Welchem Vektorfeld \(F\) entspricht das Differential \(\delta f\)? Skizzieren Sie das Vektorfeld \(F\).
Ist das Differential \(\delta f\) exakt oder inexakt bzw. das Vektorfeld \(F\) wegunabhängig oder wegabhängig? Begründen Sie Ihre Antwort mit einer Rechnung.
Berechnen Sie das Integral \(\int \delta f\) entlang des Halbkreises \(x(t) = -\cos(t)\), \(y(t) = \sin(t)\) für \(0 \leq t \leq \pi\) von \((-1, 0)\) nach \((1, 0)\).
Berechnen Sie das Integral \(\int \delta f\) entlang einer anderen Kurve von \((-1, 0)\) nach \((1, 0)\).
Aufgabe AI2: Kraftfeld¶
Welche Arbeit verrichtet das Kraftfeld \(F(x,y,z)= \begin{pmatrix} xy \\ 1 \\ yz \end{pmatrix}\) an einer Masse, wenn diese längs der Schraubenlinie \(x(t) = \cos(t)\), \(y(t) = \sin(t)\), \(z(t) = t\) für \(0 \leq t \leq 2\pi\) bewegt wird?
Quelle: Papula: Mathematik für Naturwissenschaftler - Band 3, Auflage 6, 2011, p.244, Aufgabe 8.
Aufgabe AI3: Thermodynamik - Ideales Gas¶
Der Zustandsraum eines Mols eines idealen Gases kann als der positive Quadrant \(\mathbb{R}_+^2\) mit den Koordinatenachsen \(V\) und \(p\) modelliert werden.
Zustandsgrößen:
Die Temperatur ist aufgrund der Idealen-Gas-Gleichung \(pV = RT\) für ein Mol durch \(T(V,p)= \frac{pV}{R}\) als Funktion von \(V\) und \(p\) auf dem Zustandsraum gegeben, wobei \(R\) die Gaskonstante ist.
Die innere Energie ist die Funktion \(U(V,p)=\frac{3}{2}pV\).
Die Entropie ist die Funktion \(S(V,p)=\frac{3}{2}R\ln(pV^{\frac{5}{3}})\).
Das Gas ist anfangs im Zustand \((V_1,p_1)=(1,32)\) und expandiert in den Zustand \((V_2,p_2)=(8,1)\). Berechnen Sie die vom Gas geleistete Arbeit und die vom Gas absorbierte Wärme für folgende Prozesse:
Zuerst wird der Druck des Gases isochor von \(p_1=32\) auf \(p_2=1\) verringert, anschließend wird das Volumen isobar von \(V_1=1\) auf \(V_2=8\) vergößert.
Zuerst expandiert das Gas isotherm zum Volumen \(V_2=8\), danach wird der Druck \(p\) bei konstantem Volumen zu 1 reduziert.
Das Gas expandiert adiabatisch von \((V_1,p_1)=(1,32)\) zu \((V_2,p_2)=(8,1)\).
Überprüfen Sie Ihre Ergebnisse jeweils mittels der Beziehung \(\Delta U = Q - W\).
Aufgabe AI4: Thermodynamik - Entropiefunktion¶
Zeigen Sie, dass es sich beim Differential \(\frac{C_V}{T}\,\text{d}T + \frac{R}{V}\,\text{d}V\) um das exakte Differential \(\text{d}S\) einer von \(T\) und \(V\) abhängigen Funktion \(S(T,V)\) handelt.
Bestimmen Sie diese Funktion \(S(T,V)\).
Zeigen Sie, dass Ihr Ergebnis für \(S(T,V)\) bis auf eine additive Konstante der in der vorigen Aufgabe angegebenen Entropiefunktion \(S(V,p)=\frac{3}{2}R\log(pV^{\frac{5}{3}})\) entspricht.
Hinweise: \(S(T,V)\) ist die Entropiefunktion in Abhängigkeit von \(T\) und \(V\) eines Mols eines idealen Gases und gehört zu den thermodynamischen Zustandsgrößen. \(T\): absolute Temperatur, \(V\): Volumen, \(R\): allgemeine Gaskonstante; \(C_V\): Wärmekapazität eines Mols bei konstantem Volumen. Für ein Mol lautet die ideale Gasgleichung \(pV = RT\) und \(C_V=\frac{3}{2}R\).
Quelle: Papula: Mathematik für Naturwissenschaftler - Band 3, Auflage 6, 2011, p.244, Aufgabe 6. Lesen Sie evtl. auf Seite 157f. das Beispiel (1) als Vorbereitung.
Aufgabe AI5: Thermodynamik - ideales Gas¶
Für ein Mol lautet die ideale Gasgleichung \(pV = RT\). Das Arbeitsdifferential ist \(\delta W = pdV\), und das Wärmedifferential ist \(\delta Q = \frac{5}{2}pdV + \frac{3}{2}Vdp\). Die innere Energie ist \(U=\frac{3}{2}pV\).
Das Gas ist ursprünglich im Zustand \((V_1,p_1)=(8,1)\) und wird in den folgenden zwei Schritten in den Zustand \((V_2,p_2)=(1,32)\) gebracht: zuerst Druckerhöhung bei konstantem Volumen auf \(p=4\), anschließend isotherme Kompression bis zum Volumen \(V_2=1\).
Zeichnen Sie den Gesamtprozess in einem \(p\)-\(V\)-Diagramm ein. In welchem Zustand ist das Gas nach dem ersten Schritt? Welche Temperatur hat es in diesem Zustand? Welche Temperatur hat es im Endzustand?
Berechnen Sie die Arbeit \(W\) und die Wärme \(Q\) in jedem Schritt. Überprüfen Sie Ihre Ergebnisse in jedem Schritt mittels der Beziehung \(\Delta U = Q - W\).
Aufgabe AI6: Thermodynamik - Schwarzkörperstrahlung¶
Die elektromagnetische Strahlung in einem Brennofen mit Volumen \(V\) und bei Temperatur \(T\) hat die thermodynamischen Eigenschaften eines schwarzen Körpers:
Druck: \(p = \frac{\sigma}{3}T^4\)
innere Energie: \(U = 3pV\)
Entropie: \(S = \frac{4\sigma}{3}T^3V\)
Dabei bezeichnet \(\sigma\) die Stefan–Boltzmann Konstante.
Berechnen Sie \(S\) und \(T\) in \((V,p)\)-Koordinaten, d. h. als Funktionen \(S(V,p)\) and \(T(V,p)\).
Berechnen Sie das Wärmedifferential \(Q = T\text{d}S\) in \((V,p)\)-Koordinaten.
Zeigen Sie, dass \(\text{d}U = T\text{d}S - p\text{d}V\) gilt.
Zu Beginn habe der schwarze Körper das Volumen \(V_0\) und die Temperatur \(T_0\). Das Volumen wird nun adiabatisch (also bei konstanter Entropie) auf \(V_1=64V_0\) erhöht. Bestimmen Sie die zugehörige Endtemperatur \(T_1\) und die während der Expansion vom schwarzen Körper verrichtete Arbeit.
Aufgabe AI7: Vergleich von Wegen¶
Berechnen Sie \(\int_{(0,1)}^{(1,2)} (x^2 -y)\,\text{d}x + (y^2 + x)\,\text{d}y\)
entlang einer geraden Linie von \((0,1)\) nach \((1,2)\).
entlang der zwei geraden Linien von \((0,1)\) nach \((1,1)\) und von \((1,1)\) nach \((1,2)\).
Ist das obige Arbeitsintegral wegunabhängig oder wegabhängig? Begründen Sie Ihre Antwort.
Quelle: Schaum’s Outlines: Advanced Mathematics for Engineers and Scientists. Aufgabe 6.10., S. 160f.
Aufgabe AI8: Potentialfunktion¶
Gegeben ist das Differential \((3y^2 - 12x)\,\text{d}x + (6xy + 1)\,\text{d}y\).
Gibt es eine Potentialfunktion? Wenn ja, bestimmen Sie eine, wenn nein, begründen Sie Ihre Antwort.
Lösungen¶
Lösung AI1: Weg(un)abhängige Vefktorfelder bzw. (in)exakte Differentiale¶
\(F = \begin{pmatrix} y \\ -x \end{pmatrix}\). Siehe Code.
inexakt bzw. wegabhängig, da \(\text{rot}(F) = -2 \neq 0\).
\(s(t)= \begin{pmatrix} -\cos(t)(t) \\ \sin(t) \end{pmatrix}\), \(\int \delta f = \int_0^\pi \sin^2(t) + \cos^2(t)\,\text{d}t = \int_0^\pi 1\,\text{d}t = \pi\)
z.B. direkte Verbindung mit \(s(t)= \begin{pmatrix} t \\ 0 \end{pmatrix}\) für \(-1 \leq t \leq 1\), \(\int \delta f = \int_{-1}^1 0\,\text{d}t = 0.\)
x = linspace(-1, 1, num=11)
y = linspace(-1, 1, num=11)
X, Y = meshgrid(x, y)
Vx = Y
Vy = -X
figure(figsize=(4,4))
Q = quiver(X, Y, Vx, Vy, scale=5) # für unskalierten Plot verwende units='xy', scale=1
xlabel('x')
ylabel('y')
grid(True)
Lösung AI2: Kraftfeld¶
Siehe Papula: Mathematik für Naturwissenschaftler - Band 3, Auflage 6, 2011, I Vektoranalysis, Übungsaufgaben zu Abschnitt 7, Aufgabe 8: S. 244 und S. 779. Ergebins: \(-2\pi\)
Lösung AI3: Thermodynamik - Ideales Gas¶
Siehe AI3_1.jpg und AI3_2.jpg.
Teil (a) isotchor: \(Q=-\frac{3}{2}31\), \(W=0\)
Teil (b) isobar: \(Q=\frac{5}{2}7\), \(W=7\)
Teil (a) isotherm: \(Q=32\ln(8)\), \(W=32\ln(8)\)
Teil (b) isochor: \(Q=-36\), \(W=0\)
\(Q=0\), \(W=36\)
Lösung AI4: Thermodynamik - Entropiefunktion¶
Siehe AI4.jpg.
Da \(\text{rot}\begin{pmatrix} \frac{C_V}{T} \\ \frac{R}{V} \end{pmatrix} = 0\), ist das Differential exakt.
\(S(T,V) = C_V\ln(T) + R\ln(V) + C\) mit \(C\) einer Konstanten.
Lösung AI5: Thermodynamik - ideales Gas¶
Siehe AI5.jpg.
\((V,p)=(8,4)\), \(T=32/R\)
Teil (a) isochor: \(Q=36\), \(W=0\)
Teil (b) isotherm: \(Q=-32\ln(8)\), \(W=-32\ln(8)\)
Lösung AI6: Thermodynamik - Schwarzkörperstrahlung¶
Siehe AI6.jpg.
\(S(V,p) = 4\sqrt[4]{\frac{\sigma}{3}}p^{3/4}V\), \(T(V,p)=\sqrt[4]{\frac{3}{\sigma}}p^{1/4}\)
\(Q = T\,\text{d}S = 4p\,\text{d}V + 3V\,\text{d}p\)
\(T\,\text{d}S - p\,\text{d}V = 3p\,\text{d}V + 3V\,\text{d}p = \text{d}(3pV) = \text{d}U\)
Endtemperatur \(T_1=\frac{T_0}{4}\) , Arbeit \(W=\frac{3}{4}\sigma T_0^4 V_0\)
Lösung AI7: Vergleich von Wegen¶
Siehe AI7.jpg.
5/3; -2/3 und 10/3
wegabhängig aufgrund der vorherigen Aufgabe
Lösung AI8: Potentialfunktion¶
Siehe AI8.jpg.
Ja, weil exaktes Differential. Potentialfunktion: \(3xy^2 - 6x^2 + y\)
Kurztestfragen¶
Welches Differential entspricht dem Vektorfeld \(F:\mathbb{R}^2 \rightarrow \mathbb{R}^2: F(x, y) = \begin{pmatrix} yx \\ -x \end{pmatrix}\)?
Ist das Differential \(xy\,\text{d}x - y\,\text{d}y\) exakt oder inexakt? Begründen Sie Ihre Antwort.
Was unterscheidet eine Zustandsgröße von einer Prozessgröße?
Kann ein Gradientenfeld Wirbel haben? Begründen Sie Ihre Antwort.
Welches Vektorfeld entspricht dem Differential \(-x^3\,\text{d}x + \frac{y}{x}\,\text{d}y\)?
Ist das Vektorfeld \(F:\mathbb{R}^2 \rightarrow \mathbb{R}^2: F(x, y) = \begin{pmatrix} yx \\ -x \end{pmatrix}\) konservativ? Begründen Sie Ihre Antwort.
Was berechnen die Operatoren div, grad und rot von was?
Besitzt das Differential \(-yx^3\,\text{d}x + \frac{x}{y}\,\text{d}y\) eine Potentialfunktion? Begründen Sie Ihre Antwort.
Ist das Differential \(6xy\,\text{d}x + 3x^2\,\text{d}y\) exakt? Begründen Sie Ihre Antwort.
Berechnen Sie \(\int\limits_{(0,0)}^{(1,2)} 6xy\,\text{d}x + 3x^2\,\text{d}y\) entlang eines Weges Ihrer Wahl.
Bestimmen Sie die Potentialfunktion des exakten Differentials \(x y^2\,\text{d}x + x^2 y \,\text{d}y\).
Berechnen Sie \(\int\limits_{(0,0)}^{(2,1)}x y^2\,\text{d}x + x^2 y \,\text{d}y\) entlang eines Weges Ihrer Wahl.
Ist das Differential \(6y^2\,\text{d}x - 12xy\,\text{d}y\) exakt oder inexakt? Existiert zu diesem Differential eine Stammfunktion \(f(x,y)\)?
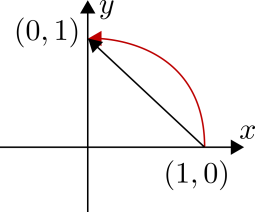
Parametrisieren Sie die eingezeichnete Kurve in Abhängigkeit des Winkels \(\varphi\) gemäß \(\left(\begin{array}{c} x(\varphi) \\ y(\varphi) \end{array}\right)\). Geben Sie auch den Wertebereich von \(\varphi\) an.

Was unterscheidet eine Zustandsgröße von einer Prozessgröße?
Das Differential \(x\,\text{d}x - y\,\text{d}y\) entspricht einem Vektorfeld. Dieses Vektorfeld kann als Kraftfeld interpretiert werden.
Zeigen Sie rechnerisch, dass das Kraftfeld wegunabhängig ist.
Wird das Kraftfeld entlang des eingezeichneten Viertelkreises durchlaufen, dann wird eine Arbeit von \(-1\) verrichtet. Zeigen Sie rechnerisch, dass die Arbeit gleich groß ist, wenn das Kraftfeld entlang einer Geraden von \((1,0)\) nach \((0,1)\) durchlaufen wird. Parametrisieren Sie dazu zunächst die Gerade mit \(\left(\begin{array}{c} x \\ y(x) \end{array}\right)\). Berechnen Sie dann das Integral \(\int x\,\text{d}x - y\,\text{d}y\) entlang der Geraden von \((1,0)\) nach \((0,1)\).