Contents

Lineare gewöhnliche Differentialgleichungen 2. Ordnung - Vorlesung

Lineare gewöhnliche Differentialgleichungen 2. Ordnung - Vorlesung

Themenüberblick:

  • Einführungsbeispiel: Schwingung, Exponentialansatz

  • Lösungsstruktur: homogene (Exponentialansatz) und partikuläre Lösungen, allgemeine Lösung, Anfangswertproblem

  • Übungsbeispiele

zusätzliche Unterlagen: 16_Differentialgleichungen_Teil_2-scan.pdf

%pylab inline
%config InlineBackend.figure_format = 'svg'

%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib

Einführungsbeispiel: gedämpfte harmonische Schwingung

Modellierung:

Die eindimensionale Bewegung eines Massenpunktes unter dem Einfluss

  • einer Reibungskraft, die proportional zu seiner Geschwindigkeit ist, und

  • einer linearen Rückstellkraft

ist ein Beispiel einer gedämpften harmonischen Schwingung. Um die zugehörige DGL zu bestimmen, verwenden wir Netwons Bewegungsgleichung und erhalten:

\[m\ddot{y}(t) = -d\dot{y}(t) -ky(t).\]

  • \(m\) … Masse des Massenpunkts

  • \(y(t)\) … eindimensionaler Ort zum Zeitpunkt \(t\)

  • \(-d\dot{y}(t)\) … Reibungskraft mit positiver Konstante \(d\)

  • \(-ky(t)\) … lineare Rückstellkraft mit positiver Konstante \(k\)

Auch in der Elektrotechnik gibt es Schwingungen. Zum Beispiel der Strom \(i(t)\) als Funktion der Zeit \(t\) im RLC-Schwingkreis erfüllt die DGL \(LC\frac {d^{2}i}{dt^{2}}(t) + RC\frac {di}{dt}(t) + i(t) = 0\) , ebenfalls eine gedämpfte harmonische Schwingung.

Die DGL einer gedämpften harmonischen Schwingung ist ein Beipiel einer linearen GDGL 2-ter Ordnung mit konstanten Koeffizienten. Letztere hat die Standardform

\[\ddot{y} + a\dot{y} + by = c.\]

Exponentialansatz:

Zur Bestimmung der Bewegung des Massenpunktes schreiben wir zuerst die Bewegungsgleichung in Standardform:

\[\ddot{y} + \frac{d}{m}\dot{y} + \frac{k}{m}y = 0.\]

Dann untersuchen wir, ob und - falls ja - für welche Werte von \(\lambda\) der Ansatz \(y(t)=e^{\lambda t}\) die DGL löst. Einsetzen des Ansatzes in die DGL liefert

\[\begin{split}\begin{align} \lambda^2 e^{\lambda t} + \frac{d}{m} \lambda e^{\lambda t} + \frac{k}{m} e^{\lambda t} &= 0 \\ \lambda^2 + \frac{d}{m} \lambda + \frac{k}{m} &= 0 \\ \lambda_{1,2} &= -\frac{d}{2m} \pm \sqrt{\frac{d^2 - 4mk}{4m^2}} \\ \lambda_{1,2} &= -\frac{d}{2m} \pm \sqrt{-1}\frac{\sqrt{4mk - d^2}}{2m} \\ \lambda_{1,2} &= -\frac{d}{2m} \pm i \omega. \end{align}\end{split}\]

Dabei haben wir \(\omega := \frac{\sqrt{4mk - d^2}}{2m}\) definiert und haben zudem angenommen, dass \(d^2 \leq 4mk\) gilt, d. h. dass die Dämpfung im Vergleich zur Rückstellkraft und Masse schwach ist. Unter dieser Annahme ist \(\omega\) reell, größer gleich Null und wird als die Kreisfrequenz der gedämpften Schwingung bezeichnet. Die Kreisfrequenz der ungedämpften Schwingung mit \(d=0\) hat den Wert \(\omega_0 = \frac{\sqrt{4mk - 0}}{2m} = \sqrt{\frac{k}{m}}.\) Wir bemerken, dass \(\omega_0 \geq\omega\) gilt, Dämpfung die Kreisfrequenz also verkleinert.

Die allgemeine Lösung der Bewegungsgleichung ist die Linearkombination der beiden Exponentialfunktionen \(e^{\lambda_1 t}\) und \(e^{\lambda_2 t}\):

\[y(t) = C_1 e^{\lambda_1 t} + C_2 e^{\lambda_2 t},\]

wobei die Konstanten \(C_1\) und \(C_2\) komplexe Zahlen sind. Da die DGL linear ist, sind sowohl der Real- als auch der Imaginäranteil einer Lösung wieder Lösung. Die allgemeine relle Lösung lautet daher

\[y(t) = e^{-\frac{d}{2m}t} \left[c_1 \cos(\omega t) + c_2 \sin(\omega t)\right]\]

mit reellen Konstanten \(c_1\) und \(c_2\). Sie besteht aus der exponentiellen Dämpfung \(e^{-\frac{d}{2m}t}\) und der harmonischen Schwingung \(c_1 \cos(\omega t) + c_2 \sin(\omega t)\) mit Kreisfrequenz \(\omega\).

Analyse am Computer: mit SymPy

import sympy as sp
sp.init_printing()

t, m, d, k = sp.symbols('t m d k')
y = sp.symbols('y', cls=sp.Function)

diffeq = sp.Eq(m*y(t).diff(t).diff(t), -d*y(t).diff(t) - k*y(t))
diffeq
_images/13_lineare_GDGL_2_vl_8_0.png 
sp.dsolve(diffeq, y(t))
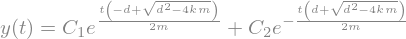
_images/13_lineare_GDGL_2_vl_9_0.png

Zahlenbeispiel:

diffeq_bsp = diffeq.subs('m', 4).subs('d', 2).subs('k', 4)
diffeq_bsp
_images/13_lineare_GDGL_2_vl_11_0.png 
y_bsp = sp.dsolve(diffeq_bsp, y(t))
y_bsp
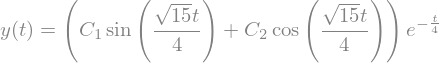
_images/13_lineare_GDGL_2_vl_12_0.png 
rcParams['figure.figsize'] = 5, 3

y_plot = y_bsp.subs('C1', -2).subs('C2', 2)
sp.plot(y_plot.args[1], (t, 0.0, 15.0), xlabel="t", ylabel="y");
_images/13_lineare_GDGL_2_vl_14_0.svg

Beispiele mit Inhomogenität = treibende Kraft:

if True: # mit Dämpfung
    diffeq = sp.Eq(y(t).diff(t).diff(t), 
                   -0.25*y(t).diff(t) - 4*y(t) + 1/10*sp.sin(2*t)) 
else:    # Resonanz
    diffeq = sp.Eq(y(t).diff(t).diff(t), 
                   -0.00*y(t).diff(t) - 4*y(t) + sp.sin(2*t)) 

diffeq
_images/13_lineare_GDGL_2_vl_16_0.png 
y_bsp = sp.dsolve(diffeq, y(t))
y_bsp
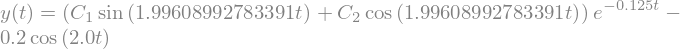
_images/13_lineare_GDGL_2_vl_17_0.png 
y_plot = y_bsp.subs('C1', 1).subs('C2', 1)
sp.plot(y_plot.args[1], (t, 0.0, 70.0), xlabel="t", ylabel="y");
_images/13_lineare_GDGL_2_vl_18_0.svg

Lösungsstruktur

Homogen mit konstanten Koeffizienten:

Die allgemeine Lösung der homogenen linearen DGL 2-ter Ordnung mit konstanten Koeffizienten

\[\ddot{y}(t) + a \dot{y}(t) + by(t) = 0\]

ist von der Form

\[y(t) = c_1 y_1(t) + c_2 y_2(t).\]

Dabei bezeichnen \(y_1(t)\) und \(y_2(t)\) zwei sogenannte Fundamentallösungen. Die allgemeine Lösung ist also eine Linearkombination von zwei Fundamentallösungen. Diese sind Lösungen der DGL und erfüllen die Eigenschaft

\[\begin{split}\det\begin{pmatrix} y_1 (t) & y_2 (t) \\ \dot{y_1}(t) & \dot{y_2}(t) \end{pmatrix} \neq 0.\end{split}\]

Jedes Anfangswertproblem läßt sich wegen dieser Eigenschaft eindeutig lösen.

Der Lösungsansatz \(e^{\lambda t}\) (Exponentialansatz) führt zur charakteristischen Gleichung

\[\lambda^2 + a \lambda + b = 0\]

mit Lösungen \(\lambda_1\) und \(\lambda_2\) und folgenden zugehörigen Fundamentallösungen:

  • \(\lambda_1\) und \(\lambda_2\) ungleich und reell: \(y_1(t)=e^{\lambda_1 t}\) und \(y_2(t)=e^{\lambda_2 t}\)

  • \(\lambda_1=\lambda_2=:\lambda\) und reell: \(y_1(t)=e^{\lambda t}\) und \(y_2(t)=te^{\lambda t}\)

  • \(\lambda_{1,2} = \beta\pm i\omega\): \(y_1(t)=e^{\beta t}\cos(\omega t)\) und \(y_2(t)=e^{\beta t}\sin(\omega t)\)

Inhomogen mit konstanten Koeffizienten:

Die allgemeine Lösung der inhomogenen linearen DGL 2-ter Ordnung mit konstanten Koeffizienten

\[\ddot{y}(t) + a \dot{y}(t) + by(t) = g(t)\]

ist von der Form

\[y(t) = y_h(t) + y_p(t).\]

Dabei ist \(y_h(t)\) die allgemeine Lösung der zugehörigen homogenen DGL \(\ddot{y}(t) + a \dot{y}(t) + by(t) = 0\) und \(y_p(t)\) eine partikuläre Lösung der inhomogenen DGL. Für letztere gibt es unterschiedliche Ansätze je nach der Form von \(g(t)\), siehe Literatur.

Übungsbeispiele

Aufgaben:

  • Bestimmen Sie die allgemeine Lösung der DGL:

    • \(\ddot{y}(t) + 5 \dot{y}(t) + 6y(t) = 0\)

    • \(\ddot{y}(t) + 4 \dot{y}(t) + 4y(t) = 0\)

  • Bestimmen Sie die Lösung der DGL \(\ddot{y}(t) + 4 \dot{y}(t) + 13y(t)=0\), welche die Anfangsbedingungen \(y(0)=1\) und \(\dot{y}(0)= 10\) erfüllt.

t = sp.symbols('t')
y = sp.symbols('y', cls=sp.Function)
diffeq = sp.Eq(y(t).diff(t).diff(t) + 5*y(t).diff(t) + 6*y(t), 0)
# diffeq = sp.Eq(y(t).diff(t).diff(t) + 4*y(t).diff(t) + 4*y(t), 0)
diffeq
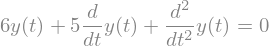
_images/13_lineare_GDGL_2_vl_21_0.png 
sp.dsolve(diffeq, y(t))
_images/13_lineare_GDGL_2_vl_22_0.png 
y = sp.exp(-2*t)*sp.cos(3*t) + 4*sp.exp(-2*t)*sp.sin(3*t)
y.subs(t, 0).evalf()
_images/13_lineare_GDGL_2_vl_23_0.png 
y.diff(t).subs(t, 0).evalf()
_images/13_lineare_GDGL_2_vl_24_0.png 
sp.init_printing(False)

Allgemeine Schwingungsgleichung und Resonanz:

Die DGL einer mechanischen Schwingung und eines elektrischen Schwingkreises lassen sich auf folgende, oft verwendete allgemeine Form bringen:

\[\ddot{y} + 2\delta \dot{y} + \omega_0^2 y = 0.\]

  • Aufgabe 1: Für welche Werte von \(\delta\) und \(\omega_0\) schwingt das System, d. h. die charakteristischen Gleichung hat komplexe Lösungen? Bestimmen Sie die Frequenz \(\omega\) für diesen Fall.

    Lösung: \(\lambda_{1,2} = -\delta \pm \sqrt{\delta^2 - \omega_0^2}\), \(\delta^2 < \omega_0^2\), \(\omega=\sqrt{\omega_0^2 - \delta^2}\)

    Literatur: Dietmaier: Mathematik für Angewandte Wissenschaften. p. 440f.

  • Aufgabe 2: Für diesen Fall wird die allgemeine Lösung oft in der Form

    \[y(t) = e^{-\delta t}[c_1 \cos(\omega t) + c_2 \sin(\omega t)]\]

    als auch

    \[y(t) = Ae^{-\delta t}\cos(\omega t - \varphi)\]

    geschrieben. Wie hängen diese zwei zusammen? Interpretieren Sie die beiden Formen und machen Sie Beispielplots.

    Lösung: \(c_1 = A\cos(\varphi)\), \(c_2 = A\sin(\varphi)\), Additionstheorem \(\cos(\omega t)\cos(\varphi) + \sin(\omega t)\sin(\varphi) = \cos(\omega t - \varphi)\)

    Literatur: Dietmaier: Mathematik für Angewandte Wissenschaften. p. 440f.

t = linspace(0, 10, 500)
A = 2              # Anfangsamplitude
delta= 0.2         # Dämpfungsfaktor
omega = 2*pi/3     # Kreisfrequenz
phi = pi           # Phasenverschiebung
y = A*exp(-delta*t)*cos(omega*t - phi)

figure(figsize=(5,3))
plot(t, y)
xlabel('t')
ylabel('y')
ylim(-A,A)
grid(True)
_images/13_lineare_GDGL_2_vl_28_0.svg

  • Aufgabe 3: Eine harmonisch erzwungene Schwingung hat die allgemeine Form

    \[\ddot{y} + 2\delta \dot{y} + \omega_0^2 y = a\cos(\tilde{\omega}t).\]

    Eine partikuläre Lösung lautet

    \[y_p(t) = A\cos(\tilde{\omega}t - \varphi)\]

    mit

    \[A = \frac{a}{\sqrt{(\omega_0^2 - \tilde{\omega}^2)^2 +4\delta^2\tilde{\omega}^2 }}.\]

    Bei welchem Wert der Erregerfrequenz \(\tilde{\omega}\) ist die Amplitude \(A\) maximal, d. h. herrscht Resonanz?

    Lösung: Ableiten nach \(\tilde{\omega}\) liefert die Resonanzfrequenz \(\omega_r= \sqrt{\omega_0^2 - 2\delta^2} < \omega < \omega_0\)

    Literatur: Papula: Band2 IV, 4.1.4; Feynman: The Feynman Lectures on Physics, Vol. 1, Chapter 23 Resonance

# delta < omega_0:
delta   = 0.15
omega_0 = 3
omega_t = linspace(0, 10, num=500)
a       = 1

A = a/sqrt( (omega_0**2 - omega_t**2)**2 + 4*delta**2*omega_t**2 )
omega_r = sqrt(omega_0**2 - 2*delta**2)

figure(figsize=(6,4))
plot(omega_t, A, label='Amplitude A')
y0, y1 = ylim()
vlines(omega_r, y0, y1, linestyle='--', label='Resonanzfrequenz $\omega_r$')
ylim(y0, y1)
xlabel('Erregerfrequenz')
legend()
grid(True)
_images/13_lineare_GDGL_2_vl_30_0.svg

previous

Lineare gewöhnliche Differentialgleichungen 1. Ordnung - Übungen

next

Lineare gewöhnliche Differentialgleichungen 2. Ordnung - Übungen