Contents

Allgemeine gewöhnliche Differentialgleichungen - Vorlesung

Allgemeine gewöhnliche Differentialgleichungen - Vorlesung

Themenüberblick:

  • Beispiele

  • Klassifizierung und Begriffe

  • grafische Darstellung: Richtungsfeld, Integralkurve

  • Lösungsmethoden: am computer und analytisch mit Trennung der Variablen und Integration exakter gewöhnlicher Differentialgleichungen

zusätzliche Unterlagen: 15_Differentialgleichungen_Teil_1-scan.pdf

%pylab inline
%config InlineBackend.figure_format = 'svg'

%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib

Beispiele

Newtonsche Bewegungsgleichung mit konstanter Kraft:

Auf einen Massenpunkt mit Masse \(m\), der sich entlang einer 1-dimensionalen Bahn (Straße, Schiene, Seilbahn etc.) mit Ortskoordinate \(x\) bewegen kann, wirke eine konstante Kraft \(F\) in Richtung der Bahn. Seine Bewegung wird durch eine Funktion \(x(t)\) beschrieben, die jedem Zeitpunkt \(t\) den (Aufenthalts-)Ort \(x(t)\) zuordnet. Die Newtonsche Bewegungsgleichung (Newtons zweites Gesetz) besagt, dass die Ortsfunktion \(x(t)\) die folgende Gleichung, genannt Bewegungsgleichung, erfüllt

\[m\ddot{x}(t) = F.\]

Mit dem Lösen der Bewegungsgleichung ist das Bestimmen jener Funktion(en) \(x(t)\) gemeint, die die Bewegungsgleichung und evtl. zusätzliche Bedingungen (Anfangs- oder Randbedingungen) erfüllen. Da in der Bewegungsgleichung Ableitungen der gesuchten Funktion \(x(t)\) vorkommen, ist sie ein Beispiel für eine Differentialgleichung (DGL).

Lösung:

  • allgemeine Lösung: durch zweimaliges Integrieren erhält man \(x(t) = \frac{F}{2m}t^2 + C_1 t + C_2\) mit Integrationskonstanten \(C_1\) und \(C_2\)

  • partikuläre Lösung für Anfangsbedingungen \(x(0)=2\) (Anfangsort) und \(\dot{x}(0)=5\) (Anfangsgeschwindigkeit): \(x(t) = \frac{F}{2m}t^2 + 5 t + 2\)

Newtonsche Bewegungsgleichung mit linearer Rückstellkraft:

  • Bewegungsgleichung: \(m\ddot{x}(t) = -kx(t)\), Federkonstante \(k>0\)

  • allgemeine Lösung: Definiere den Parameter \(\omega:=\sqrt{\frac{k}{m}}\). Dann ist die allgemeine Lösung durch \(x(t) = C_1 \cos(\omega t) + C_2 \sin(\omega t)\) gegeben.

Newtons Abkühlgesetz:

Wir suchen die Temperatur \(T_W(t)\) einer Tasse Glühwein als Funktion der Zeit \(t\). Der Glühwein befindet sich in einer Umgebung mit konstanter Umgebungstemperatur \(T_U\). Newtons Abkühlgesetz besagt, dass der Energieverlust pro Zeit durch Wärmeübertragung an die Umgebung, geschrieben als \(\dot{Q}(t)\), die Gleichung

\[\dot{Q}(t) = -d [T_W(t) - T_U]\]

mit einer positiven Konstante \(d\) (Abkühlkoeffizient) erfüllt. Aus \(\dot{Q}(t) = cm\dot{T_W}(t)\) (\(m\) die Masse des Glühweins, \(c\) seine spezifische Wärmekapazität) folgt

\[cm\dot{T_W}(t) = -d [T_W(t) - T_U]\]

als Differentialgleichung für die Temperatur \(T_W(t)\).

Wir führen die Temperaturdifferenz zur Umgebung als neue abhängige Variable ein: \(T(t) := T_W(t) - T_U\), und beachten, dass \(\dot{T}(t) = \dot{T_W}(t)\) gilt. Dadurch erhalten wir die kompaktere Differentialgleichung

\[\dot{T}(t) = -\lambda T(t)\]

mit dem einzigen Parameter \(\lambda=\frac{d}{cm}\), der den Zeitverlauf bestimmt.

Lösung: \(T(t) = T(0)e^{-\lambda t}\), d. h. die Temperaturdifferenz zur Umgebung klingt exponentiell vom Anfangswert \(T(0)\) ab. Je größer \(\lambda\) ist, umso schneller kühlt der Glühwein aus.

Wärmeleitungsgleichung:

Wir betrachten einen isolierten Metallstab mit Orstkoordinate \(x\) und Temperaturverteilung \(T_0(x)\) zum Anfangszeitpunkt \(t=0\). Gesucht ist die daraus resultierende Temperaturverteilung zu späteren Zeitpunkten \(t\) an jedem betrachteten Ort \(x\), also eine Funktion \(T(x,t)\), die \(T(x,0) = T_0(x)\) erfüllt. Die Dynamik (=zeitliche Entwicklung) wird durch die Wärmeleitungsgleichung

\[\frac{\partial T}{\partial t} = a\frac{\partial^2 T}{\partial x^2}\]

beschrieben. Diese ist eine sogenannte partielle Differentialgleichung. Der Parameter \(a>0\) bezeichnet die Temperaturleitfähigkeit des Metallstabs. Die Wärmeleitungsgleichung besagt z. B., dass die zweite Ableitung (Krümmung) nach dem Ort zu einer zeitlichen Temperaturänderung führt:

  • Falls \(\frac{\partial^2 T}{\partial x^2}(x,t) > 0\), dann ist zum Zeitpunkt \(t\) die Temperatur in der Umgebung von \(x\) größer als bei \(x\), und die Temperatur steigt mit der Zeit an: \(\frac{\partial T}{\partial t} > 0\).

  • Falls \(\frac{\partial^2 T}{\partial x^2}(x,t) < 0\), dann ist zum Zeitpunkt \(t\) die Temperatur in der Umgebung von \(x\) kleiner als bei \(x\), und die Temperatur fällt mit der Zeit ab: \(\frac{\partial T}{\partial t} < 0\).

In drei Raumdimensionen wird eine Funktion \(T(x,y,z,t)\) gesucht, die die Wärmeleitungsgleichung

\[\frac{\partial T}{\partial t} = a\left[\frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2}\right] = a\Delta T\]

erfüllt. Der Operator \(\Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\) ist der sogenannte Laplace-Operator. Aus dem Gradienten von \(T(x,y,z,t)\) bezüglich den drei kartesichen Raumkoordinaten kann man den Wärmefluss \(q\) (z. B. in Watt pro Quadratmeter) an jedem Ort und zu jedem Zeitpunkt bestimmen:

\[q = -k\nabla T.\]

Der Parameter \(k\) bezeichnet die Wärmeleitfähigkeit.

Klassifizierung und Begriffe

Eine gewöhnliche Differentialgleichung (GDGL, englisch ordinary differential equation (ODE)) beschreibt das Verhalten einer Funktion, die von einer einzigen Variablen abhängt. Eine partielle Differentialgleichung (PDGL, englisch partial differential equation (PDE)) beschreibt das Verhalten einer Funktion, die von mehr als einer Variablen abhängt.

Lineare Differentialgleichungen enthalten nur lineare Terme der gesuchten Funktion und ihrer (partiellen) Ableitungen. Alle anderen Differentialgleichungen heißen nicht-lineare Differentialgleichungen.

Beispiele:

  • \(y'(x) = xy(x) + 1\) oder kürzer \(y' = xy + 1\) ist linear

  • \(y'' + xy + y^2=0\) ist nicht-linear

  • \(\frac{\text{d}y}{\text{d}x} = -\frac{x}{y}\) ist nicht-linear

  • \(x^3\frac{\text{d}y}{\text{d}x} + \sin(x) y = e^x\) ist linear

Die Ordnung der höchsten vorkommenden (partiellen) Ableitung bezeichnet die Ordnung einer DGL.

Beispiele:

  • \(y' = xy + 1\) ist von 1. Ordnung

  • \(y'' + xy + y^2=0\) ist von 2. Ordnung

  • \(\frac{\partial T}{\partial t} = a\frac{\partial^2 T}{\partial x^2}\) ist von 2. Ordnung

Die allgemeine Lösung einer GDGL enthält eine oder mehrere Integrationskonstanten, deren Werte durch Vorgaben von Anfangs- und/oder Randbedingungen bestimmt werden können. Eine partikuläre Lösung enthält keine unbestimmten Integrationskonstanten.

Das Paket aus GDGL + Anfangs- und/oder Randbedingungen heißt Anfangs- bzw. Randwertproblem. Seine Lösung liefert die zugehörige eindeutige partikulare Lösung, sofern die Anfangs- und/oder Randbedingungen dafür ausreichend und nicht überbestimmend sind.

Grafische Darstellung

Eine GDGL erster Ordnung für die gesuchte Funktion \(y(x)\) ist von der Form

\[y'(x) = f(x,y(x)).\]

Dabei ist \(f\) eine vorgegebene Funktion, die die Steigung \(y'(x)\) von \(y(x)\) an jedem Punkt in der \((x,y)\)-Ebene angibt.

Beispiele:

  • \(y'(x) = x + y^2(x) \quad\Rightarrow\quad f(x,y) = x + y^2\)

  • \(y'(x) = xy(x) \quad\Rightarrow\quad f(x,y) = xy\)

Wir können alternativ die Ableitung \(y'(x)\) als \(\frac{\text{d}y}{\text{d}x}\) schreiben und erhalten nach Multiplikation mit \({\text{d}x}\) die Differential-Gleichung

\[\text{d}y = f(x,y(x))\,{\text{d}x}.\]

An jedem Punkt der \((x,y)\)-Ebene wird dadurch ein Verhältnis zwischen der \(x\)-Änderung \(\text{d}x\) und der \(y\)-Änderung \(\text{d}y\) vorgeschrieben, das durch die Tangenten an die Lösung \(y(x)\) erfüllt werden muss.

Das Skalarfeld \(f(x,y)\) gibt somit an jedem Punkt \((x,y)\) eine Steigung bzw. Richtung vor und wird als Richtungsfeld der zugehörigen GDGL bezeichnet.

Die Lösung einer GDGL heißt auch Integralkurve.

Beispiel exponentielles Wachstum/Zerfall: Für eine Konstante \(a\) betrachten wir die GDGL \(y' = ay.\) Das Richtungsfeld \(f(x,y)=ay\) hängt nur von \(y\) ab. Die Integralkurven sind \(y(x)= Ce^{ax}\) mit der Integrationskonstanten \(C\), die gleich dem Anfangswert \(y(0)\) ist.

a = 0.10
x = arange(-2, 8, 0.5)
y = arange(-5, 5, 0.5)
X, Y = meshgrid(x, y)

dX = ones(X.shape)
dY = a*Y

# zwei Integralkurven
C_1 = 1.5
y_lsg_1 = C_1*exp(a*x)
C_2 = -2
y_lsg_2 = C_2*exp(a*x)


figure(figsize=(4,4))
quiver(X, Y, dX, dY, headwidth=0.0, scale = 20, pivot='middle', label='Richtungsfeld')
plot(x, y_lsg_1, label='Lösung 1')
plot(x, y_lsg_2, label='Lösung 2')
xlabel('x')
ylabel('y')
axis('equal')
legend(loc='best')
grid(True)
_images/11_allgemeine_GDGL_vl_9_0.svg

Lösungsmethoden

Übersicht:

  • Lösung am Computer

    • numerisch

    • symbolisch

  • Analytische Lösungsmethoden, die wir behandeln:

    • Trennung der Variablen

    • exakte Differentialgleichungen

Numerische Lösung: z. B. mit der SciPy-Funktion odeint

from scipy.integrate import odeint

Für eine Konstante \(a\) und Anfangsbedingung \(y(0)=y_0\) lösen wir die GDGL \(y' = ay.\)

# Definition der Ableitungsfunktion:
def fun(y, x): # Achtung! Die Reihenfolge der Argumente muss (y, x) sein.
    return a*y

# A sequence of time points for which to solve for y. 
# The initial value point should be the first element of this sequence.
x = arange(0, 8, 0.5) 

# The initial value:
y0 = -1.5  

# Solve numerically with odeint:
y_num = odeint(fun, y0, x)

# Vergleich mit analytischer Lösung:
y_lsg = y0*exp(a*x)

figure(figsize=(4,4))

quiver(X, Y, dX, dY, headwidth=0.0, scale = 20, pivot='middle')
plot(x, y_num, '-o', label='numerische Lösung')
plot(x, y_lsg, '-',  label='analytische Lösung')
xlabel('x')
ylabel('y')
legend()
axis('equal');
_images/11_allgemeine_GDGL_vl_15_0.svg

Symbolische/Analytische Lösung: mit SymPy

import sympy as sp

sp.init_printing()   # initializes pretty printing

x, a = sp.symbols('x a')
y = sp.symbols('y', cls=sp.Function)

diffeq = sp.Eq(y(x).diff(x), a*y(x))
diffeq
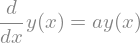
_images/11_allgemeine_GDGL_vl_20_0.png 
y_sol = sp.dsolve(diffeq, y(x))
y_sol
_images/11_allgemeine_GDGL_vl_21_0.png 
sp.init_printing(False)   # stops pretty printing

Trennung der Variablen:

Diese Methode setzt voraus, dass sich in einer GDGL \(y' = f(x,y)\) nach Umformen zu \(\text{d}y = f(x,y)\,{\text{d}x}\) die Variablen \(y\) und \(x\) auf je eine Gleichungsseite trennen lassen. Anschließend kann jede Seite über ihre Variable integriert werden.

Beispiel 1:

\[\begin{split}\begin{align} y' &= 2y \\ \text{d}y &= 2y\,\text{d}x \\ \frac{1}{y}\text{d}y &= 2\,\text{d}x \\ \int\frac{1}{y}\text{d}y &= \int 2\,\text{d}x \\ \ln|y|&= 2x + C \\ |y| &= e^{C + 2x} \\ y &= \pm e^{C}e^{2x} \\ y &= y(0)e^{2x} \end{align}\end{split}\]

Hier ist der Fall \(y(0)=0\) ausgeschlossen.

Beispiel 2: Die GDGL \(3y' + y^4\cos(x)=0\) mit Anfangsbedingung \(y(\frac{\pi}{2})=\frac{1}{2}\) kann durch Trennung der Variablen gelöst werden. Ergebnis: \(y(x) = \dfrac{1}{\sqrt[3]{\sin(x) + 7}}\)

Exakte Gewöhnliche Differentialgleichungen:

Diese Methode setzt voraus, dass eine GDGL \(y' = f(x,y)\) nach Umformen zu \(\text{d}y - f(x,y)\,{\text{d}x} = 0\) einem exakten Differential \(\text{d}y - f(x,y)\,{\text{d}x}\) entspricht. Dann ist nämlich die Bedingung \(\text{d}y - f(x,y)\,{\text{d}x} = 0\) gleichbedeutend mit \(\text{d}F = 0\) für eine zu findende Funktion \(F(x,y).\) Die Integralkurven der GDGL sind die Konturlinien von \(F\), weil sich entlang dieser \(F\) nicht ändert, also \(\text{d}F\) gleich Null ist.

Beispiel 1: In der GDGL \(\dot{y}=\frac{2t + y}{y - t}\) lassen sich die Variablen nicht trennen. Sie ist aber eine exakte GDGL.

\[\begin{split}\begin{align} \dot{y} &= \frac{2t + y}{y - t} \\ (y - t)\,\text{d}y &= (2t + y)\,\text{d}t \\ (2t + y)\,\text{d}t + (t - y)\,\text{d}y &= 0 \end{align}\end{split}\]
# Richtungsfeld:

t = arange(-3.25, 3.25, 0.5)
y = arange(-3.00, 3.00, 0.5)
T, Y = meshgrid(t, y)
dT = (  Y - T)/sqrt( (Y - T)**2 + (2*T + Y)**2 )
dY = (2*T + Y)/sqrt( (Y - T)**2 + (2*T + Y)**2 )

figure(figsize=(4,4))
quiver(T, Y, dT, dY, headwidth=0.0, scale = 10, pivot='middle')
xlabel('t')
ylabel('y')
grid(False)
_images/11_allgemeine_GDGL_vl_26_0.svg

Das Differential \((2t + y)\,\text{d}t + (t - y)\,\text{d}y\) ist exakt, was mit dem Rotatonskriterium nachgeprüft werden kann:

\[\begin{split}\begin{pmatrix}\frac{\partial}{\partial t} \\ \frac{\partial}{\partial y}\end{pmatrix} \times \begin{pmatrix} 2t + y \\ t - y \end{pmatrix} = 1 - 1 = 0.\end{split}\]

Daher gibt es eine Funktion \(F(t,y)\) mit \(\text{d}F = (2t + y)\,\text{d}t + (t - y)\,\text{d}y.\) Durch ein Wegintegral von z. B. \((0,0)\) nach \((t,y)\) über einen rechteckigen Weg erhalten wir \(F(t,y) = t^2 + yt - \frac{y^2}{2} + C\) mit \(C\) einer Integrationskonstanten:

\[\begin{split}\begin{align} F(t,y) &= \int_{(0,0)}^{(t,y)} \text{d}F \\ &= \int_{(0,0)}^{(t,y)} (2t + y)\,\text{d}t + (t - y)\,\text{d}y \\ &= \int_{(0,0)}^{(t,0)} (2t + y)\,\text{d}t + (t - y)\,\text{d}y + \int_{(t,0)}^{(t,y)} (2t + y)\,\text{d}t + (t - y)\,\text{d}y \\ &= \int_0^t (2t + 0)\,\text{d}t + \int_0^y (t - y)\,\text{d}y \\ &= t^2 \Big|_{t=0}^{t=t} + (ty -\frac{y^2}{2})\Big|_{y=0}^{y=y} + C\\ &= t^2 + ty -\frac{y^2}{2} + C \end{align}\end{split}\]
figure(figsize=(4,4))

# Richtungsfeld:
t = arange(-3.25, 3.25, 0.5)
y = arange(-3.00, 3.00, 0.5)
T, Y = meshgrid(t, y)
dT = (  Y - T)/sqrt( (Y - T)**2 + (2*T + Y)**2 )
dY = (2*T + Y)/sqrt( (Y - T)**2 + (2*T + Y)**2 )
quiver(T, Y, dT, dY, headwidth=0.0, scale = 10, pivot='middle')

# Konturlinien von F(t,y):
t = arange(-3.25, 3.25, 0.05)
y = arange(-3.00, 3.00, 0.05)
T, Y = meshgrid(t, y)
F = T**2 + T*Y - 1/2*Y**2
contour(T, Y, F, 15, cmap= 'Blues')

xlabel('t')
ylabel('y')
grid(False)
_images/11_allgemeine_GDGL_vl_28_0.svg

Die Konturlinien von \(F\) und somit die Lösungen der GDGL sind gegeben durch \(y(t) = t \pm \sqrt{3t^2 + D}\) für konstante Werte von \(D\):

\[\begin{split}\begin{align} t^2 + ty -\frac{y^2}{2} + C &= \tilde{C} \\ y^2 - 2ty - 2t^2 - 2[C - \tilde{C}] &= 0 \\ y(t) &= t \pm \sqrt{t^2 + 2t^2 + 2[C - \tilde{C}]} \\ y(t) &= t \pm \sqrt{3t^2 + D} \end{align}\end{split}\]

Beispiel 2: Die GDGL \(y' = ay\) entspricht \(-ay\,\text{d}t + \text{d}y = 0\). Das Differential \(-ay\,\text{d}t + \text{d}y\) ist nicht exakt, da

\[\begin{split}\begin{pmatrix}\frac{\partial}{\partial t} \\ \frac{\partial}{\partial y}\end{pmatrix} \times \begin{pmatrix} -ay \\ 1 \end{pmatrix} = 0 + a = a,\end{split}\]

kann aber durch Herausheben von \(y\) (bzw. durch das Multiplizieren mit \(\frac{1}{y}\), einem sogenannten integrierenden Faktor) geschrieben werden als \(y\left[-a\,\text{d}t + \frac{1}{y}\text{d}y\right]\). Die GDGL entspricht somit

\[y\left[-a\,\text{d}t + \frac{1}{y}\text{d}y\right] = 0.\]

Entweder ist nun \(y=0\) oder \(-a\,\text{d}t + \frac{1}{y}\text{d}y=0\): Der erste Fall entspricht der Lösung \(y(t)=0\). Der zweite Fall entspricht einer exakten GDGL, da

\[\begin{split}\begin{pmatrix}\frac{\partial}{\partial t} \\ \frac{\partial}{\partial y}\end{pmatrix} \times \begin{pmatrix} -a \\ 1/y \end{pmatrix} = 0 - 0 = 0.\end{split}\]

Die Lösung dieser exakten GDGL ist \(y(t) = De^{at}\) für eine Konstante \(D\neq 0\), denn auch ohne Wegintegral können wir schließen, dass:

\[\begin{split}\begin{align} -a\,\text{d}t + \frac{1}{y}\text{d}y &= 0\\ \text{d}\left(-at + \ln|y| \right) &= 0 \\ -at + \ln|y| &= C \\ \ln|y| &= C + at\\ |y| &= e^{C + at} = e^C e^{at} \\ y(t) &= \pm e^C e^{at} \\ y(t) &= D e^{at} \end{align}\end{split}\]

Insgesamt erhalten wir \(y(t) = De^{at}\) für eine beliebige Konstante \(D\), die dem Anfangswert \(y(0)\) entspricht, der nun auch Null sein kann.

Beispiel 3: 1-dimensionaler Massenpunkt in einem ortsabhängigen Kraftfeld: Die Bewegungsgleichung \(m\ddot{x}=F(x)\) ist eine GDGL zweiter Ordnung. Durch das Einführen der zusätzlichen Funktion \(v(t)\) (Geschwindigkeit) können wir die Bewegungsgleichung zu zwei GDGL erster Ordnung umformen.

\[\begin{split}\begin{align} \dot{x}=v &\quad m\dot{v}=F(x) \\ \text{d}x = v\,\text{d}t &\quad m\,\text{d}v = F(x)\,\text{d}t \end{align}\end{split}\]

Nach Multiplizieren von \(m\,\text{d}v = F(x)\,\text{d}t\) mit \(v\) und Ersetzen von \(v\,\text{d}t\) auf der rechten Seite durch \(\text{d}x\) erhalten wir

\[\begin{split}\begin{align} mv\,\text{d}v &= F(x)\,\text{d}x \\ mv\,\text{d}v - F(x)\,\text{d}x &= 0 \end{align}\end{split}\]

Dies ist eine exakte GDGL, da

\[\begin{split}\begin{pmatrix}\frac{\partial}{\partial v} \\ \frac{\partial}{\partial x}\end{pmatrix} \times \begin{pmatrix} mv \\ -F(x) \end{pmatrix} = 0 - 0 = 0.\end{split}\]

Eine Stammfunktion \(-U(x)\) von \(F(x)\) heißt in der Physik potentielle Energie der Kraft \(F(x)\) und erfüllt also \(F(x)=-U'(x)\). Mit ihr erhalten wir

\[\begin{split}\begin{align} \text{d}\left(m\frac{v^2}{2}\right) - \text{d}\left(-U(x)\right) &= 0 \\ \text{d}\left(m\frac{v^2}{2} + U(x)\right) &= 0 \end{align}\end{split}\]

Die Lösungen der Bewegungsgleichungen sind somit Konturlinien der Funktion

\[E(x, v) = m\frac{v^2}{2} + U(x),\]

die als Gesamtenergie des Massenpunktes am Ort \(x\) mit Geschwindigkeit \(v\) bezeichnet wird. Entlang jeder Integralkurve der Bewegungsgleichung ist also die Gesamtenergie erhalten: \(m\frac{v(t)^2}{2} + U(x((t)) = E_0\) für eine konstante \(E_0\) wie Energie.

Beispiel: Die lineare Rückstellkraft \(F(x) = -kx\) mit Federkonstante \(k>0\) hat die potentielle Energie \(U(x)=\frac{k}{2}x^2\). Die Gesamtenergie lautet \(E(x, v) = m\frac{v^2}{2} + k\frac{x^2}{2}\), deren Konturlinien Ellipsen im Phasenraum (=Ort-Geschwindigkeits-Diagramm) sind.

# Konturlinien von E(x,v):

m = 3
k = 1

x = arange(-3, 3, 0.1)
v = arange(-3, 3, 0.1)
X, V = meshgrid(x, v)
E = 0.5*m*V**2 + 0.5*k*X**2

figure(figsize=(4,4))
contour(X, V, E, linspace(0,20, num=25), cmap= 'jet')
xlabel('x')
ylabel('v')
grid(True)
_images/11_allgemeine_GDGL_vl_32_0.svg

previous

Integralsätze - Übungen

next

Allgemeine gewöhnliche Differentialgleichungen - Übungen