Lineare Algebra II - Übungen
Contents
Lineare Algebra II - Übungen¶
%pylab inline
%config InlineBackend.figure_format = 'svg'
%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib
Aufgaben¶
Aufgabe LA2-1: Gausssches Eliminationsverfahren¶
Bestimmen Sie von Hand mit Hilfe des Gaußschen Eliminationsverfahrens, ob folgendes lineares Gleichungssystem nicht-triviale Lösungen hat.
Überprüfen Sie Ihr Ergebnis am Computer mit Hilfe der Befehle det, inv, solve und matrix_rank.
Aufgabe LA2-2: Existenz und Eindeutigkeit von linearen Gleichungssystemen¶
Gegeben ist das lineare Gleichungssystem:
Hat das lineare Gleichungssystem für alle Vektoren \(b\) eine eindeutige Lösung? Wie können Sie dieses Problem am Computer lösen?
Aufgabe LA2-3: Reaktionsgleichungen¶
Chemische Reaktionsgleichungen beschreiben die Verhältnisse der Reaktanten und Produkte einer gegebenen Stoffumwandlung. Zum Beispiel reagiert bei der Verbrennung das Gas Propan (\(C_3 H_8\)) mit molekularem Sauerstoff (\(O_2\)) zu Kohlendioxid (\(CO_2\)) und Wasser (\(H_2 O\)), beschrieben durch die Reaktionsgleichung:
Um die Reaktion ins Gleichgewicht zu bringen, gilt es die ganzzahligen Lösungen \(x_1,...,x_4\) zu finden, so dass die Gesamtzahlen von Kohlenstoff, Wasserstoff und Sauerstoff auf der rechten und linken Seite der Reaktionsgleichung übereinstimmen. Eine systematische Methode, um das Reaktionsgleichgewicht zu bestimmen, ist die Formulierung einer vektoriellen Gleichung, welche die Zahlen der Atome aller Elemente in der Reaktion beschreibt.
Überprüfen Sie, ob folgende vektorielle Gleichung die obige Reaktion beschreibt!
\[\begin{split}x_1 \begin{pmatrix} 3 \\ 8 \\ 0 \end{pmatrix} + x_2 \begin{pmatrix} 0 \\ 0 \\ 2 \end{pmatrix} = x_3 \begin{pmatrix} 1 \\ 0 \\ 2 \end{pmatrix} + x_4 \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix}.\end{split}\]Bestimmen Sie die Lösungsmenge in \(\mathbb{R}^4\).
Finden Sie die Lösung mit kleinstmöglichen ganzen Zahlen \(x_1,...,x_4\).
Aufgabe LA2-4: Elektrischer Schaltkreis¶
Der elektische Schaltkreis in der folgenden Abbildung ist parametrisiert durch: \(U_1=230\), \(U_2=370\), \(R_1=200\), \(R_2=100\), \(R_3=300\).
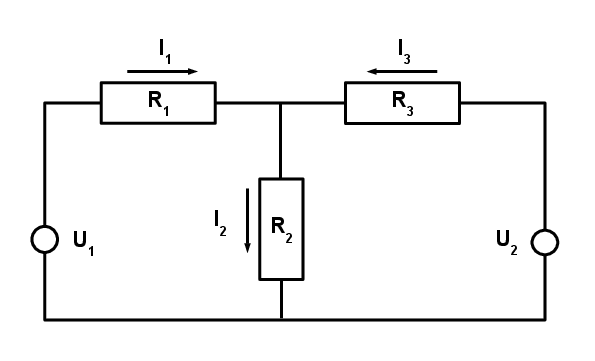
Formulieren Sie das lineare Gleichungssystem für die Stromstärken \(I_1\), \(I_2\), und \(I_3\) in Matrizenschreibweise \(Ax=b\).
Lösen Sie \(Ax=b\) händisch.
Lösen Sie \(Ax=b\) in Python mit dem Befehl
solve.Bestimmen Sie in Python die Determinante von \(A\) mit Hilfe des NumPy-Befehls
det.
Aufgabe LA2-5: Inverse einer 2x2 Matrix¶
Überprüfen Sie, dass die Inverse einer 2x2 Matrix \(A = \begin{pmatrix} a & b\\ c & d \end{pmatrix}\) durch folgende Formel gegeben ist:
\[\begin{split}A^{-1} = \frac{1}{\det(A)}\begin{pmatrix} d & -b \\ -c & a \end{pmatrix} \text{ mit } \det(A) = ad - cb.\end{split}\]Benutzen Sie diese Formel, um die Inverse der Matrix \(A = \begin{pmatrix} 0.5 & 0\\ 0 & 3 \end{pmatrix}\) zu bestimmen. Beschreiben Sie die Abbildung \(f(x)=Ax\) in Worten.
Aufgabe LA2-6: Rotationen in der Ebene¶
Betrachten Sie die Rotationsmatrix
Welche Rotation beschreibt die Abbildung \(f(x) = Rx\)?
Zeigen Sie, dass \(R^T R=I\) gilt, und berechnen Sie \(\det(R)\) sowie \(R^{-1}\)!
Aufgabe LA2-7: Leontief Modell¶
Nehmen Sie an, ein Staat ist Standort für drei verchiedene Industriesektoren: Chemische Industrie, Nahrungsmittelindustrie und Ölindustrie. Die Produktion einer Einheit Chemikalien benötigt 0.2 Einheiten von Chemikalien, 0.4 Einheiten Nahrungsmittel und 0.5 Einheiten Öl. Diese Größen werden in die erste Spalte der Verbrauchsmatrix \(A\) ein, die den Verbrauch während der Produktion wiedergibt:
Bemerkung: Die Verbrauchsmatrix der USA im Jahr 1958 enthielt 83 industrielle Sektoren, heutige Modelle sind bei weitem umfangreicher.
Es stellt sich die Frage, ob die so beschriebene Volkswirtschaft einen Bedarf \(d = \begin{pmatrix} d_1\\ d_2 \\ d_3 \end{pmatrix}\) für chemische Produkte, Nahrungsmittel und Öl decken kann? Dazu muss neben dem Produktionsplan \(p = \begin{pmatrix} p_1\\ p_2 \\ p_3 \end{pmatrix}\) der Verbrauch \(Ap\) während der Produktion berücksichtigt werden. Die Netto-Produktion von \(p - Ap\) soll daher den Bedarf \(d\) decken. Damit gilt es für einen gegebenen Bedarf \(d\) einen Produktionsplan \(p\) zu finden, so dass folgendes erfüllt ist:
Der Bedarfsvektor \(d\) und die Verbrauchsmatrix \(A\) dürfen keine negativen Einträge haben, um wirtschaftlich sinnvoll interpretiert werden zu können. Ebenso der Produktionsplan \(p = (I - A)^{-1}d\). Daher lautet die Frage: Wann ist \((I - A)^{-1}\) eine nicht-negative Matrix, d. h. jeder der Einträge ist nicht-negativ.
Berechnen Sie mit Python den Produktionsplan für den Bedarf \(d = \begin{pmatrix} 4\\ 2 \\ 3 \end{pmatrix}\). Benutzen Sie dazu den Befehl
solve.Berechnen Sie mit dem Python-Befehl
inv\((I - A)^{-1}\). Ist die Matrix nicht-negativ?Ändern Sie die Verbrauchsmatix \(A\) zu einer nicht-negativen Verbrauchsmatrix \(B\), die den Bedarf nicht decken kann.
Bemerkung: Die Matrix \(I - A\) wird Technologiematrix genannt. Sie führt einen Produktionsplan in einen Vektor über, der angibt, welcher Bedarf erfüllt werden kann.
Aufgabe LA2-8: lineare Gleichungssysteme¶
Bestimmen Sie, ohne das linearen Gleichungssystem zu lösen, ob es lösbar ist und, falls ja, eindeutig lösbar ist.
\[\begin{split}\begin{pmatrix} -10 & 3 \\ -5 & 4 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -3,5 \\ 9,2 \end{pmatrix}\end{split}\]Geben Sie ein Zahlenbeispiel für ein lineares Gleichungssystem in Matrixform an, das 2 Gleichungen, 3 Variablen und keine Lösung hat.
Geben Sie ein Zahlenbeispiel für ein lineares Gleichungssystem in Matrixform an, das mindestens 2 Gleichungen, mindestens 2 Variablen und einen 1-dimensionalen Lösungsraum hat.
Aufgabe LA2-9: Diskrete Dynamische Systeme, Eigenwerte und -vektoren¶
Jedes Jahr ziehen etwa 10 % der Bevölkerung einer Stadt in die umliegenden Vororte, und etwa 20 % der Vorstadtbevölkerung in die Stadt. Im Jahr 2016 gibt es 10 Millionen Menschen in der Stadt und 8 Millionen Menschen in den Vororten, was wir mit dem Zustandsvektor \(x_0 = \begin{pmatrix} 10 \\ 8 \end{pmatrix}\) modellieren.
Bestimmen Sie die Übergangsmatrix \(M\), so dass \(Mx\) der Einwohnerverteilung ein Jahr nach \(x\) entspricht.
Analysieren Sie das Langzeitverhalten des dynamischen Systems mit Hilfe der Eigenwerte und -vektoren von \(M\), d. h. wohin tendiert der Zustandsvektor für große Zeiten?
Quelle: David Lay, Linear Algebra and Its Applications, 4th edition, p.87, exercise 10
Aufgabe LA2-10: lineare (Un-)Abhaengigkeit¶
Sind die folgenden drei Vektoren linear abhängig oder linear unabhängig? Begründen Sie Ihre Antwort.
Aufgabe LA2-11: Orthogonale Matrizen¶
Zeigen Sie, dass die Matrix \(A = \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix}\) orthogonal ist, d. h. dass \(A^T=A^{-1}\) gilt.
Aufgabe LA2-12: Eigenwerte und -vektoren, Invertierbarkeit, Eindeutigkeit der Lösung¶
Gegeben ist die Matrix \(A= \left( \begin{matrix} 1&0&2 \\ 0&2&0 \\ 0&1&3 \end{matrix} \right)\).
Berechnen Sie von Hand und am Computer die Eigenwerte und Eigenvektoren von A.
Ist die Matrix A invertierbar? Begründen Sie Ihre Antwort.
Besitzt das Gleichungssystem \(Ax=b\) eine eindeutige Lösung? Begründen Sie Ihre Antwort.
Hinweis:
Aufgabe LA2-13: Existenz einer Lösung¶
Bestimmen Sie, ohne das Gleichungssystem zu lösen, ob eine Lösung existiert.
Aufgabe LA2-14: Lineare Abhängigkeit¶
Für welche Werte von \(h\) sind die folgenden Vektoren linear abhängig?
Hinweis:
Aufgabe LA2-15: Eigenwerte und -vektoren¶
Bestimmen Sie von Hand und in Python alle Eigenwerte und -vektoren folgender Matrix.
Aufgabe LA2-16: Eigenwerte und -vektoren¶
Bestimmen Sie alle Eigenwerte und -vektoren folgender Matrix.
Quelle: Papula, Band 2, 7.2, S. 128 f.
Lösungen¶
Lösung LA2-1: Gaußsches Eliminationsverfahren¶
Das Gaußschen Eliminationsverfahrens liefert, dass das Gleichungssystem nicht-triviale Lösungen hat, nämlich alle Vielfachen von \(x = \begin{pmatrix} -17 \\ 6 \\ 8 \end{pmatrix}.\) Siehe auch Code.
# matrix form Ax=b of the system of linear equations:
A = array([[ 2, -5, 8],
[-2, -7, 1],
[ 4, 2, 7]])
b = zeros((3,1))
# check if (-17, 6, 8) is a solution:
x = array([-17, 6, 8])
print("Ax = {}".format(A@x)) # should be zero as the system is Ax=0
# From det(A) = 0 it follows that Ax=0 has infinitly many solutions:
print("Determinante = {}".format(det(A)))
# Erinnerung: Rang einer Matrix = Anzahl der linear unabhängigen Spalten- oder Zeilenvektoren
# Ax=b hat unendlich viele Lösungen, wenn Rang(A)=Rang(A|b)<Anzahl Variablen.
print("Rang(A) =", matrix_rank(A))
Ab = hstack((A, b))
print("Rang(Ab) =", matrix_rank(Ab))
# Conlusion: Ax=b has infinitly many solutions.
# inv(A) # -> LinAlgError: Singular matrix, can also be seen from det(A)=0
# solve(A, b) # -> LinAlgError: Singular matrix, can also be seen from det(A)=0
Ax = [0 0 0]
Determinante = 0.0
Rang(A) = 2
Rang(Ab) = 2
Lösung LA2-2: Existenz und Eindeutigkeit von linearen Gleichungssystemen¶
Siehe Code. Das lineare Gleichungssystem \(Ax=b\) hat nicht für alle Vektoren \(b\) eine eindeutige Lösung, denn der Rang von \(A\) ist kleiner als die Anzahl an Spalten von \(A\), bzw. die Determinante von \(A\) ist Null.
A = array([[ 2, -4, -2],
[-5, 1, 1],
[ 7, -5, -3]])
print("rank(A) = {}".format(matrix_rank(A)))
print("det(A) = {}".format(det(A)))
rank(A) = 2
det(A) = -3.996802888650562e-15
Lösung LA2-3: Reaktionsgleichungen¶
Die vektorielle Gleichung entspricht den Massenbilanzen für die drei Elemente \(C\), \(H\) und \(O\).
Das Gaußschen Eliminationsverfahren liefert, dass das lineare Gleichungssystem eine 1-dimensionale Lösungsmenge hat, die z. B. mit \(x_4\) parametrisiert werden kann:
\[\begin{split}\begin{align} x_4 & = \text{frei wählbar} \\ x_3 & = 0.75 x_4 \\ x_2 & = 1.25 x_4 \\ x_1 & = 0.25 x_4 \end{align}\end{split}\]Lösung mit kleinstmöglichen ganzen Zahlen: \(x_1 = 1, x_2 = 5, x_3 = 3,x_4 = 4\).
Lösung LA2-4: Elektrischer Schaltkreis¶
Das lineare Gleichungssystem
hat die eindeutige Lösung \(I_1=0.5\), \(I_1=1.3\), \(I_3=0.8\), siehe auch Code.
Die Matrixform lautet
# matrix form:
A = array([[ 1, -1, 1],
[200, 100, 0],
[ 0, 100, 300]])
b = array([0, 230, 370])
# det(A) is not zero. Therefore, Ax=b has a unique solution.
print("det(A) = {}".format(det(A)))
# The unique solution can be computed via solve():
I = solve(A, b)
print("I = {}".format(I))
det(A) = 109999.99999999991
I = [0.5 1.3 0.8]
Lösung LA2-5: Inverse einer 2x2 Matrix¶
Berechne \(A^{-1}A\) und \(AA^{-1}\). Beides ergibt die Einheitsmatrix.
\(A^{-1} = \begin{pmatrix} 2 & 0 \\ 0 & \frac{1}{3} \end{pmatrix}\), siehe Code. Stauchen in \(x_1\)-Richtung um Faktor 2 und Strecken in \(x_2\)-Richtung um Faktor 3.
A = array([[0.5, 0],
[0 , 3]])
print("inv(A) = \n{}".format(inv(A)))
inv(A) =
[[2. 0. ]
[0. 0.33333333]]
Lösung LA2-6: Rotationen in der Ebene¶
Die Matrix \(R\) beschreibt die Rotation eines Vektors der Ebene um den Winkel \(\alpha\) gegen den Uhrzeigersinn. Das Drehzentrum ist der Koordinatenursprung.
Rechnung für \(R^T R=I\) händisch, \(\det(R)=1\) und \(R^{-1}= \begin{pmatrix} \cos(-\alpha) & -\sin(-\alpha) \\ \sin(-\alpha) & \cos(-\alpha) \end{pmatrix} = \begin{pmatrix} \cos(\alpha) & \sin(\alpha) \\ -\sin(\alpha) & \cos(\alpha) \end{pmatrix} = R^T\). Beispiel \(\alpha=\pi/6\): siehe Code.
alpha = pi/6
R = array([[cos(alpha), -sin(alpha)],
[sin(alpha), cos(alpha)]])
print("R = \n{}".format(R))
print("R^T R = \n{}".format(R.T@R))
print("det(R) = {}".format(det(R)))
print("inv(R) = \n{}".format(inv(R)))
R =
[[ 0.8660254 -0.5 ]
[ 0.5 0.8660254]]
R^T R =
[[1.00000000e+00 7.43708407e-18]
[7.43708407e-18 1.00000000e+00]]
det(R) = 1.0
inv(R) =
[[ 0.8660254 0.5 ]
[-0.5 0.8660254]]
Lösung LA2-7: Leontief Modell¶
Siehe Code.
A = array([[.2 , .3 , .4],
[.4 , .4 , .1],
[.5 , .1 , .3]])
d = array([[4, 2, 3]]).T
p = solve(eye(3) - A, d)
print("p = \n{}".format(p))
p =
[[31.72043011]
[29.67741935]
[31.1827957 ]]
inv(eye(3) - A) # is non-negative
array([[4.40860215, 2.68817204, 2.90322581],
[3.5483871 , 3.87096774, 2.58064516],
[3.65591398, 2.47311828, 3.87096774]])
B = array([[.2 , .9 , .4],
[.4 , .4 , .1],
[.5 , .1 , .3]])
d = array([[4, 2, 3]]).T
p = solve(eye(3) - B, d)
print("p = \n{}".format(p))
p =
[[-37.80952381]
[-26.28571429]
[-26.47619048]]
inv(eye(3) - B) # has negative entries
array([[-3.9047619 , -6.38095238, -3.14285714],
[-3.14285714, -3.42857143, -2.28571429],
[-3.23809524, -5.04761905, -1.14285714]])
Lösung LA2-8: lineare Gleichungssysteme¶
Siehe Code.
\(\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}\begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 10 \\ 20 \end{pmatrix}\). Die beiden Gleichungen entsprechen zwei parallelen Ebenen im Raum.
\(\begin{pmatrix} 1 & 2 \\ 2 & 4 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3 \\ 6 \end{pmatrix}\). Die zweite Gleichung ist ein Vielfaches der ersten, die einer Geraden in der Ebene entspricht.
A = array([[-10, 3],
[ -5, 4]])
print("det(A) = {}".format(det(A))) # is negative => Ax=b has a unique solution.
det(A) = -25.000000000000007
Lösung LA2-9: Diskrete Dynamische Systeme, Eigenwerte und -vektoren¶
# initial state_
x0 = array([[10],
[8]])
# transition matrix:
M = array([[0.9, 0.2],
[0.1, 0.8]])
# dynamics:
n = 50 # number of years
times = arange(n) # vector of years from now
X = zeros((2,n)) # matrix with states as columns
X[:,[0]] = x0 # put initial state into first column
for k in range(1, n): # iterate over years
X[:,[k]] = M@X[:,[k - 1]]
figure(figsize=(5,3))
plot(times, X[0,:], '.-', label='Stadt')
plot(times, X[1,:], '.-', label='Vororte')
legend(loc='best')
xlabel('Zeit [Jahr]')
ylabel('Anzahl Menschen [Mio.]')
ylim(0,13)
grid(True)
# eigenvalues and eigenvectors:
L, V = eig(M)
print("eigenvalues = {}".format(L))
print("matrix with eigenvectors in columns = \n{}".format(V))
eigenvalues = [1. 0.7]
matrix with eigenvectors in columns =
[[ 0.89442719 -0.70710678]
[ 0.4472136 0.70710678]]
# rescaling of eigenvestors:
e0 = V[:,[0]] # first column
e0 = e0/sum(e0)
e1 = array([[-1],
[ 1]])
E = hstack((e0, e1))
print("matrix with rescaled eigenvectors in columns = \n{}".format(E))
matrix with rescaled eigenvectors in columns =
[[ 0.66666667 -1. ]
[ 0.33333333 1. ]]
# representation of the initial state x0 as a linear combination of the eigenvectors:
# y00*e0 + y10*e1 = E*y0 = x0, with y0 the column vector of the coefficients
y0 = solve(E, x0)
print("y0 = \n{}".format(y0))
y0 =
[[18.]
[ 2.]]
# The part of the linear combination belonging to eigenvalue 1 dominates.
# and forms the limit value for large times, see figure above.:
print(y0[0,0]*e0)
[[12.]
[ 6.]]
Dynamic of state evolution in the long run:
Thus, \(\lim_{t\to\infty} x_t = \lim_{t\to\infty}M^t x_0 =18 e_0 = (12, 6)^T\) as in the figure above.
Lösung LA2-10: lineare (Un-)Abhängigkeit¶
Lineare Unabhängigkeit der Vektoren \(v_i\) ist gegeben, wenn das lineare Gleichungssystem \(x_1 v_1 + x_2 v_2 + x_3 v_3 = 0\) nur die triviale Lösung \(x=0\) hat. Lösen des zugehörigen Gleichungssystems in Matrixform \(Ax=0\) (von Hand oder mit dem Computer) zeigt, dass es nur die triviale Lösung \(x=0\) hat. Alternativ kann mit der Determinante oder dem Rang argumentiert werden, siehe Code.
A = array([[2,-1,-1],
[1, 2, 2],
[0, 5,-1]])
print("det(A) = {}".format(det(A)))
# not zero => there is a unique solution to Ax=0, namely the trivial x=0
print("rank(A) = {}".format(matrix_rank(A)))
# rank(A) = rang(A|b) = n =>
# there is a unique solution to Ax=0, namely the trivial x=0
det(A) = -29.99999999999999
rank(A) = 3
Lösung LA2-11: Orthogonale Matrizen¶
Händisches Nachrechnen ergibt \(A^T A = I\) und \(AA^T = I\), was die Behauptung beweist. Siehe auch Code.
A = array([[ 1/sqrt(2), 1/sqrt(2)],
[-1/sqrt(2), 1/sqrt(2)]])
print(A.T - inv(A)) # should be the zero matrix
# Note that the typical numerical precision on a computer is at the level 1e-16.
[[-1.11022302e-16 1.11022302e-16]
[-1.11022302e-16 -1.11022302e-16]]
Lösung LA2-12: Eigenwerte und -vektoren, Invertierbarkeit, Eindeutigkeit der Lösung¶
Die drei Lösungen \(\lambda_i\) von \(\det(A - \lambda I)\) sind die Eigenwerte von \(A\): \(\lambda_1 = 1, \lambda_2 = 2, \lambda_3 = 3\). Die drei dazugehörigen Eigenvektoren \(v_i\) sind die Lösungen der linearen Gleichungssysteme \(A v_i = \lambda v_i\): z. B. \(v_1 = (1,0,0)^T, v_2 = (1,0,1)^T, v_3 = (-2,1,-1)^T\). Siehe auch Code.
Ja, denn die Determinante ist nicht Null. Verwende die Formel vom Hinweis und siehe auch den Code.
Ja, denn die Matrix ist invertierbar, weil ihre Determinante nicht Null ist. Daher läßt sich \(Ax=b\) von links mit der Inversen von \(A\) multilizieren, wodurch \(x=A^{-1}b\) als eindeutige Lösung folgt.
A = array([[1, 0, 2],
[0, 2, 0],
[0, 1, 3]])
L, V = eig(A)
print("eigenvalues of A: {}".format(L))
print("matrix with eigenvectors of A in columns: \n{}".format(V))
print("det(A) = {}".format(det(A)))
eigenvalues of A: [1. 3. 2.]
matrix with eigenvectors of A in columns:
[[ 1. 0.70710678 -0.81649658]
[ 0. 0. 0.40824829]
[ 0. 0.70710678 -0.40824829]]
det(A) = 6.0
Lösung LA2-13: Existenz einer Lösung¶
Ja, denn die Determinante der Koeffizientenmatrix ist nicht Null.
A = array([[-10, 3],
[ -5, 5]])
print("det(A) = {}".format(det(A)))
det(A) = -35.00000000000001
Lösung LA2-14: Lineare Abhängigkeit¶
Die Determinante der Vektoren-Matrix berechnet sich zu \(h+38\). Die Determinante ist für nur für \(h=-38\) Null. Für diesen Wert von \(h\) sind die Vektoren linear abhänging.
h = -38
A = array([[ 1, -3, 2],
[-2, 7, 1],
[-4, 6, h]])
print("det(A) = {}".format(det(A)))
det(A) = 0.0
Lösung LA2-15: Eigenwerte und -vektoren¶
Die zwei Lösungen \(\lambda_i\) von \(\det(A - \lambda I)\) sind die Eigenwerte von \(A\): \(\lambda_1 = -5, \lambda_2 = 9\). Die zwei dazugehörigen Eigenvektoren \(v_i\) sind die Lösungen der linearen Gleichungssysteme \(A v_i = \lambda v_i\): z. B. \(v_1 = (-1,1)^T, v_2 = (1,1)^T\). Siehe auch Code.
A = array([[2, 7],
[7, 2]])
L, V = eig(A)
print("eigenvalues of A: {}".format(L))
print("matrix with eigenvectors of A in columns: \n{}".format(V))
eigenvalues of A: [ 9. -5.]
matrix with eigenvectors of A in columns:
[[ 0.70710678 -0.70710678]
[ 0.70710678 0.70710678]]
Lösung LA2-16: Eigenwerte und -vektoren¶
Die zwei Lösungen \(\lambda_i\) von \(\det(A - \lambda I)\) sind die Eigenwerte von \(A\): \(\lambda_1 = -1\), \(\lambda_2 = 3\), Die zwei dazugehörigen Eigenvektoren \(v_i\) sind die Lösungen der linearen Gleichungssysteme \(A v_i = \lambda v_i\): \(v_1 = (-5, 1)^T\), \(v_2 = (-1, 1)^T\) Siehe auch Code.
A = array([[-2, -5],
[ 1, 4]])
L, V = eig(A)
print("eigenvalues of A: {}".format(L))
print("rescaled 1st eigenvector: \n{}".format(V[:,[0]]/sum(V[1,0])))
print("rescaled 2nd eigenvector: \n{}".format(V[:,[1]]/sum(V[1,1])))
eigenvalues of A: [-1. 3.]
rescaled 1st eigenvector:
[[-5.]
[ 1.]]
rescaled 2nd eigenvector:
[[-1.]
[ 1.]]
Kurztestfragen¶
Geben Sie ein Zahlenbeispiel für ein Matrixprodukt \(AB\), für das \(BA\) nicht dasselbe Ergebnis liefert.
Es seien \(v\) und \(w\) zwei Spaltenvektoren aus \(\mathbb{R}^n\). Welche der folgenden Ausdrücke liefern dasselbe, welche nicht? \(v^T w\), \(v w^T\), \(w^Tv\), \(w v^T\)
Ist eine Verschiebung in der Ebene, d. h. jedem Punkt \(x\) der Ebene wird sein um einen fixen Verschiebungsvektor verschobener Punkt zugeordnet, linear, also als \(Ax\) darstellbar? Begründen Sie Ihre Antwort.
Wie bestimmen Sie, ob ein quadratisches lineares Gleichungssystem keine, eine oder unendlich viele Lösungen hat?
Beschreiben Sie die Rechenschritte zur Bestimmung der Eigenvektoren einer Matrix.
Wie bestimmen Sie, ob ein allgemeines lineares Gleichungssystem keine, eine oder unendlich viele Lösungen hat?
Welche Eigenwerte hat die Matrix \(\begin{pmatrix} 1 & 3\\ 0 & -2 \end{pmatrix}\)?
Was ist der Rang einer Matrix, und wozu kann man ihn verwenden?
Was ist die Determinante einer Matrix, und wozu kann man sie verwenden?
Welche Eigenwerte hat die Matrix \(\begin{pmatrix} 1 & -2\\ 1 & 4 \end{pmatrix}\)?
Gegeben sei das Gleichungssystem \(Ax=b\). Der Rang der Koeffizientenmatrix \(A\) sei geringer als der Rang der erweiterten Koeffizientenmatrix \(A|b\) (\(\text{Rg}(A) < \text{Rg}(A|b)\)). Wie viele Lösungen hat das gegebene Gleichungssystem?
Geben Sie ein Zahlenbeispiel für ein lineares Gleichungssystem in Matrixform an, das 2 Gleichungen, 3 Unbekannte und keine Lösung hat.
Wie lautet die Rotationsmatrix einer Vektorrotation bei gegebenem Winkel \(\alpha\)? Die Rotationsmatrix \(R= \left(\begin{array}{c c} -0.707 & -0.707 \\ 0.707 & -0.707 \\ \end{array}\right)\) soll auf den Vektor \(v=\left(\begin{array}{c} 2 \\ 2 \\ \end{array}\right)\) angewendet werden. Wie lautet der resultierende Vektor?
Wie können sie zeigen, dass für die Matrix \(\left(\begin{array}{c c} 1 & 4 \\ 8 & 16 \\ \end{array}\right)\) eine inverse Matrix existiert? Berechnen Sie darüber hinaus die inverse Matrix.
Wir betrachten das Gleichungssystem \(\left(\begin{array}{c c c} 1 & 2 & 3 \\ 2 & 5 & 7 \\ 3 & 14 & 17 \\ \end{array}\right)x=\left(\begin{array}{c} 4 \\ 8 \\ 12 \\ \end{array}\right)\). Bestimmen Sie anhand des Gaußschen Eliminationverfahrens, wie viele Lösungen es für das Gleichungssystem gibt.
Programmierprojekte¶
Dynamisches System - Bevölkerungswachstum-Modell mit Leslie-Matrix¶
Die Population einer Region zerlegt sich in die Altersgruppen
jünger als 20 Jahre
20 bis 39 Jahre und
über 40 Jahre.
Anfangs ist der Generationenstand durch den Vektor \(x = \begin{pmatrix} x_1\\ x_2 \\ x_3 \end{pmatrix}\) gegeben. Eine Generation später ist die Population durch zwei Effekte verändert:
Reproduktion: \(x_1^{\text{neu}} = F_1 x_1 + F_2 x_2 + F_3 x_3\) mit den Fertilitätsraten \(F_k\).
Überlebensrate: \(x_2^{\text{neu}} = P_1 x_1\) and \(x_3^{\text{neu}} = P_2 x_2\) mit den Überlebenswahrscheinlichkeiten \(P_k\).
Die Leslie Matrix \(A\) liefert \(x^{\text{neu}}\) für \(x\) via \(x^{\text{neu}}= Ax\). Betrachten Sie folgendes Beispiel:
Aufgaben:
Der Generationenstand sei zu Beginn durch \(x = \begin{pmatrix} .6\\ 1 \\ .8 \end{pmatrix}\) [Mio. Menschen] gegeben. Benutzen Sie Python, um die absoluten und relativen Populationsgrößen aller drei Gruppen für die nächsten 30 Generationen zu berechnen und zu plotten.
Berechnen Sie die Eigenwerte und Eigenvektoren der Leslie Matrix mithilfe des Python Befehls
eig, und interpretieren Sie das Resultat. Welcher Eigenwert ist weshalb für die Bevölkerungsentwicklung entscheidend? Wie kann ein zugehöriger Eigenvektor zu diesem Eigenwert zur Prognose der sich abzeichnenden relativen Populationsgrößen verwendet werden?
Abgabe: Hochladen eines Ipython-Notebook als ipynb-Datein und aller evtl. zusätzlichen (Daten-)Files in ILIAS.
Lösung:
A = array([[0.04, 1.1 , 0.01],
[0.98, 0 , 0 ],
[0 , 0.92, 0 ]])
print(A)
(L, V) = eig(A)
for k in range(len(L)):
print("Der Eigenwert {0:0.2f} hat den Eigenvektor\n {1}".format(L[k], V[:,[k]]))
x0 = array([[0.6, 1, 0.8]]).T
#x0 = -V[:,[0]]
#x0 = V[:,[1]]
#x0 = V[:,[2]]
N = 50
X = zeros((3, N))
X[:,[0]] = x0
for k in range(1, N):
X[:,[k]] = dot(A, X[:,[k-1]])
figure(figsize(8,6))
title('Absoluter Generationenstand')
plot(X[0,:], 'g', label='Alter < 20')
plot(X[1,:], 'r', label='Alter 20 bis 39')
plot(X[2,:], 'k', label='Alter > 40')
xlabel('Generation')
ylabel('Generationenstand absolut')
legend()
grid(True)
[[0.04 1.1 0.01]
[0.98 0. 0. ]
[0. 0.92 0. ]]
Der Eigenwert 1.06 hat den Eigenvektor
[[-0.63392495]
[-0.58468167]
[-0.50624747]]
Der Eigenwert -1.01 hat den Eigenvektor
[[ 0.6083396 ]
[-0.58784241]
[ 0.53325813]]
Der Eigenwert -0.01 hat den Eigenvektor
[[ 7.76398245e-05]
[-9.09394695e-03]
[ 9.99958646e-01]]
Umskalieren der Eigenvektoren, insbesondere des Eigenvektors mit größten Eigenwert:
E = V/sum(V, axis=0)
e1 = E[:,[0]]*100
print(e1)
[[36.75238138]
[33.89745683]
[29.3501618 ]]
figure(figsize(8,6))
title('Relative Generationenstände')
plot(X[0,:]/sum(X, axis = 0)*100, 'g', label='Alter < 20')
plot(X[1,:]/sum(X, axis = 0)*100, 'r', label='Alter 20 bis 39')
plot(X[2,:]/sum(X, axis = 0)*100, 'k', label='Alter > 40')
hlines(e1[0,0], 0, N, color='g')
hlines(e1[1,0], 0, N, color='r')
hlines(e1[2,0], 0, N, color='k')
legend()
xlabel('Generation')
ylabel('Generationenstand relativ in Prozent')
grid(True)
