.ipynb .pdf

Binder

Contents

Nichtlineare Optimierung - Übungen

%pylab inline

%config InlineBackend.figure_format = 'svg'
from mpl_toolkits.mplot3d.axes3d import Axes3D
from scipy import optimize

%pylab is deprecated, use %matplotlib inline and import the required libraries.
Populating the interactive namespace from numpy and matplotlib

Aufgaben

Aufgabe NO1: Taylorreihe des Gravitationalspotentials

1. Berechnen Sie die Taylorreihe des Gravitationspotentials \(\phi(r) = -G\frac{mM_E}{r}\) eines Körpers der Masse \(m\) an der Erdoberfläche bis zur ersten Ordnung.

2. Vergleichen Sie Ihr Ergebnis mit der bekannten Formel \(mgh\), wobei \(g=9.81\frac{m}{s^2}\) die Erdbeschleunigung und \(h\) die Höhe über der Erdoberfläche sind.

3. Erstellen Sie einen Plot des wahren und approximierten Graviationspotentials in der Nähe der Erdoberfläche.

Daten: Gravitationskonstante \(G = 6{,}6742\cdot10^{-11}\;\mathrm{\frac{m^3}{kg\,s^2}}\), Masse der Erde \(M_E = 5{,}974\cdot10^{24}\;\mathrm{kg}\), Durchmesser der Erde \(d= 12714\) km

Aufgabe NO2: Maximaler Profit

Die Energie GmbH investiert 20.000 EUR in das Design und die Entwicklung eines neuen Produkts. Sie kann es für 2 EUR pro Stück herstellen. Wenn die Energie GmbH \(a\) EUR für Marketing ausgibt und das Produkt mit einem Stückpreis von \(p\) EUR anbietet, dann verkauft sie \(2000 + 4\sqrt{a} - 20p\) Stück.

1. Bestimmen Sie den Profit der Energie GmbH als Funktion \(f(a, p)\).

2. Bei welchem Stückpreis \(p\) und bei welchen Marketingkosten \(a\) ist der erzielte Profit maximal? Lösen Sie dieses Problem von Hand und numerisch mit Hilfe der Funktion root.

Aufgabe NO3: Extrema und quadratische Approximation

Gegeben ist die Funktion \(z(x,y) = -x^3 + y^2 + 12x - 6y - 5\).

1. Erstellen Sie den Graphen und den Konturplot von \(z(x,y)\) im Bereich \(x\in[-4,4]\) und \(y\in[-8,8]\).

2. Finden Sie alle kritischen Punkte von \(z(x,y)\) und bestimmen Sie, welche ein lokales Minimum, Maximum oder Sattelpunkt sind.

3. Verwenden Sie den Python-Befehl quiver, um das Gradientenfeld \(\nabla z\) in Ihren Konturplot einzuzeichnen. Hier ein Beispiel dazu für eine andere Funktion:

x = arange(0,3*pi,.25)
y = arange(0,3*pi,.25)
X,Y = meshgrid(x, y)

# Funktion z(x,y)
Z = sin(.75*X) - cos(Y)

# Gradientenfeld
U = .75*cos(.75*X)
V = sin(Y)

figure(figsize=(8,6))
CS = contour(X,Y,Z,15)
Q = quiver(X,Y, U,V)
xlabel('x')
ylabel('y')

1. Bestimmen Sie die beste quadratische Approximation an \(z(x,y)\) im Punkt \((x,y)=(-2,3)\) und inkludieren Sie diese in Ihrem Graph.

Aufgabe NO4: Wärmeverlustfunktion - Teil 2

Ein rechteckiges Industriegebäude habe die Länge \(x\), die Breite \(y\) und die Höhe \(z\). In der Tabelle ist der Wärmeverlust pro Tag durch jede Seite des Gebäudes in geeigneten Energieeinheiten pro Quadratmeter Seitenfläche angegeben.

Dach	Ostseite	Westseite	Nordseite	Südseite	Boden
10	8	6	10	5	1

Der gesamte tägliche Wärmeverlust des Gebäudes ist daher durch \(Q(x,y,z) = 11xy + 14yz +15xz\) gegeben.

Berechnen Sie die Abmessungen jenes Gebäudes mit einem Volumen von 18480 Kubikmetern, das den minimalen Gesamtwärmeverlust pro Tag hat.

Aufgabe NO5: Produktionsplan und Produktionsmöglichkeitenkurve

Ein Unternehmen stellt zwei Produkte A und B her, die das gleiche Rohmaterial verwenden. Das verfügbare Rohmaterial und die verfügbare Arbeitszeit sind begrenzt. Daher muss das Unternehmen entscheiden, wie viel seiner Ressourcen der Produktion von A und wie viel B zugeordnet werden. Es bezeichne \(x\) die Produktionsmenge von A und \(y\) die Produktionsmenge von B. Wir nehmen an, dass die Resourcenbeschränkung folgender Gleichung entspricht:

\[9x^2 + 4y^2 = 18 000.\]

Die graphische Darstellung dieser Gleichung (für \(x \geq 0\) und \(y \geq 0\)), wird als Produktionsmöglichkeitenkurve bezeichnet. Ein Punkt \((x, y)\) auf dieser Kurve stellt einen Produktionsplan für das Unternehmen dar. Der Grund für die Beziehung zwischen \(x\) und \(y\) beinhaltet die Beschränkungen für die verfügbare Arbeitszeit und das verfügbare Rohmaterial. Wir nehmen zudem an, dass pro Einheit von A ein Gewinn von 3 EUR und pro Einheit von B ein Gewinn von 4 EUR erzielt werden kann.

1. Zeichnen Sie die Produktionsmöglichkeiten-Kurve.

2. Bestimmen Sie den Produktionsplan, der den Gewinn maximiert. Wie hoch ist der maximale Gewinn?

Quelle: Goldstein, Lay, Asmar, Schneider: “Calculus & its Applications”: exercise 13 auf Seite 409

Aufgabe NO6: Preisdifferenzierung

Eine Firma vermarktet ein Produkt in zwei Ländern mit unterschiedlichen Mengen. Sei \(x\) die Stückzahl, die im ersten Land verkauft werden soll, und \(y\) die Stückzahl, die im zweiten Land verkauft werden soll. Um die Stückzahlen \(x\) und \(y\) vollständig absetzen zu können, muss die Firma den Verkaufspreis im ersten Land auf \(97 - \frac{x}{10}\) EUR/Stück und im zweiten Land auf \(83 - \frac{y}{20}\) EUR/Stück festlegen. Diese Funktionen werden Preis-Absatz-Funktion oder Nachfragefunktion genannt. Die Kosten für die Herstellung betragen \(20000 + 3(x + y)\) EUR.

1. Bestimmen Sie jene Stückzahlen \(x\) und \(y\), die den Gewinn (= Profit, = Umsatz(=Erlös) minus Kosten) maximieren. Bestimmen Sie diesen maximalen Gewinn.

2. Angenommen, die Firma muss in jedem Land den selben Preis festlegen, d.h. \(97 -\frac{x}{10} = 83 -\frac{y}{20}\). Bestimmen Sie die Werte von \(x\) und \(y\), die den Gewinn unter dieser Einschränkung maximieren. Bestimmen Sie diesen maximalen Gewinn. Warum ist er niedriger als vorher?

Quelle: Goldstein, Lay, Asmar, Schneider: “Calculus & its Applications”: example 2 auf Seite 397 und exercise 16 auf Seite 409

Aufgabe NO7: Energieversorgungsnetz

Drei Generatoren mit folgenden Kostenfunktionen in EUR/Stunde sollen eine Gesamtlast von 952 MW decken.

\[\begin{split}\begin{align} f_1(x_1) &= x_1 + 0.0625 x_1^2 \\ f_2(x_2) &= x_2 + 0.0125 x_2^2 \\ f_3(x_3) &= x_3 + 0.0250 x_3^2 \end{align}\end{split}\]

Die Variable \(x_i\) ist die Ausgangsleistung in MW des \(i\)-ten Generators. Die Funktion \(f_i\) gibt die Kosten pro Stunde des \(i\)-ten Generators an. Die Kostenfunktionen \(f_i\) wurden z.B. durch einen Polynom-Fit basierend auf den historischen Betriebsdaten erstellt.

1. Berechnen Sie den optimale Generatoreneinsatz, d.h. die optimalen Werte der \(x_i\) Variablen, so dass die Gesamtkosten pro Stunde minimal sind und die Gesamtlast gedeckt ist.

2. Berechnen Sie die entsprechenden optimalen Gesamtkosten pro Stunde.

Aufgabe NO8: Produktionsplan und Produktionsmöglichkeitenkurve

Ein Unternehmen produziert \(x\) Einheiten von Produkt A und \(y\) Einheiten von Produkt B und hat die Produktionsmöglichkeitskurve \(4x^2 + 25y^2 = 50 000\). Die Profite sind 2 EUR pro Einheit von Produkt A und 10 EUR pro Einheit von Produkt B. Bestimmen Sie den Produktionsplan maximalen Gesamtprofits und den dazugehörigen maximalen Gesamtprofit.

Aufgabe NO9: Design eines Schwimmbeckens

Ein quaderförmiges Schwimmbecken mit einem Fassungsvermögen (Volumen) von \(V = 108 \text{ m}^3\) soll so gebaut werden, dass die Oberfläche (Boden und Seitenwände) möglichst klein wird. Wie sind die Abmessungen des Beckens zu wählen?

Quelle: Papula: Klausur- und Übungsaufgaben - Auflage 4, Aufgabe E71

Aufgabe N1O: Extrema

Gesucht ist das Extremum der Funktion \(f(x, y) = 2x^2 - xy - 2y + y^2\). An welcher Stelle befindet es sich, und um welche Art von Extremum handelt es sich?

Quelle: Sanal: Mathematik für Ingenieure. p. 583, Bsp. 11.61

Lösungen

Lösung NO1: Taylorreihe des Gravitationalspotentials

1. Taylorreihe bis 1. Ordnung: \(\phi(r_E + h) \simeq \phi(r_E) + \phi'(r_E)h = -G\frac{mM_E}{r_E} + G\frac{mM_E}{r_E^2}h\)

2. Der erste Term ist eine Konstante und daher für die potentielle Energie irrelevant. Wir vergleichen den zweite Term \(G\frac{mM_E}{r_E^2}h\) mit \(mgh\). Der Term \(G\frac{M_E}{r_E^2}\) hat einen Wert von \(9.87\frac{m}{s^2}\) und ist somit vergleichbar mit \(g=9.81\frac{m}{s^2}\).

3. Siehe Code.

G  = 6.6742e-11 
ME = 5.974e24
rE = 12714.0e3/2
g = G*ME/rE**2
print(g)

9.86642938737485

m = 1
r = linspace(rE*0.75, rE*1.25)

figure(figsize=(5,3))
plot(r/1e6, -G*m*ME/r, label='wahr')
plot(r/1e6, -G*m*ME/rE + g*m*(r - rE), 'r', label='Taylorreihe 1. Ordg.')
legend(loc='best')
xlabel('Radius [Mio. m]')
ylabel('Potential')
grid(True)

Lösung NO2: Maximaler Profit

1. \(f(a,p) = -20000 + (p - 2)(2000 + 4\sqrt{a} - 20p) - a\)

2. \(\frac{\partial f}{\partial a}(a,p) = 0\) liefert \(\sqrt{a}=2(p-2)\). \(\frac{\partial f}{\partial p}(a,p) = 0\) liefert \(2040 + 4\sqrt{a} - 40p = 0\) Einsetzen der ersten in die zweite Gleichung liefert \(p = 63.25\) EUR/Stück und \(a = 15006.25\) EUR. Um sich sicher zu sein, dass an dieser Stelle ein Maximum vorliegt, berechnen wir dort die Eigenwerte der Hessematrix \(H = \begin{pmatrix} \frac{2 - p}{\sqrt{a^3}} & \frac{2}{\sqrt{a}} \\ \frac{2}{\sqrt{a}} & -40 \end{pmatrix}\), siehe Code.

p = 63.25
a = 15006.25

H = array([[ (2 - p)/a**1.5, 2/sqrt(a)], 
           [      2/sqrt(a),      -40 ]])
print("Hessian matrix at critical point = \n{}".format(H))

L, V = eig(H)
print("eigenvalues of Hessian matrix at critical point: ".format(L))

Hessian matrix at critical point = 
[[-3.33194502e-05  1.63265306e-02]
 [ 1.63265306e-02 -4.00000000e+01]]
eigenvalues of Hessian matrix at critical point: 

def my_grad(x):  # gradient, x = [a,p]
    a = x[0]
    p = x[1]
    return [2*(p - 2)/sqrt(a) - 1,
            2040 + 4*sqrt(a) - 40*p]

def my_jac(x):  # Jacobi matrix
    a = x[0]
    p = x[1]
    return array([[-(p - 2)/a**1.5, 2/sqrt(a)],
                  [2/sqrt(a)      ,      -40]])

print("without Jacobi matrix:")
sol = optimize.root(my_grad, [3, 3], jac=None)
print("return value of optimize.root() command: {}".format(sol))
print("solution x = {}".format(sol.x))
print("\n")
print("with Jacobi matrix:")
sol = optimize.root(my_grad, [3, 3], jac=my_jac)
print("return value of optimize.root() command: {}".format(sol))
print("solution x = {}".format(sol.x))

without Jacobi matrix:
return value of optimize.root() command:     fjac: array([[-0.04270997,  0.99908751],
       [-0.99908751, -0.04270997]])
     fun: array([-1.90271354e-10,  1.01226760e-09])
 message: 'The solution converged.'
    nfev: 74
     qtf: array([-7.33736389e-09, -1.05739542e-09])
       r: array([ 2.09213765e-02, -5.13968371e+01,  4.47490809e-02])
  status: 1
 success: True
       x: array([15006.25000712,    63.25      ])
solution x = [15006.25000712    63.25      ]


with Jacobi matrix:
return value of optimize.root() command:     fjac: array([[-0.0428299 ,  0.99908238],
       [-0.99908238, -0.0428299 ]])
     fun: array([ 1.99840144e-15, -4.54747351e-13])
 message: 'The solution converged.'
    nfev: 73
    njev: 1
     qtf: array([4.91562714e-09, 7.07756460e-10])
       r: array([ 2.09388279e-02, -5.13968366e+01,  5.09217328e-02])
  status: 1
 success: True
       x: array([15006.25,    63.25])
solution x = [15006.25    63.25]

Lösung NO3: Extrema und quadratische Approximation

1. Siehe Code

2. \(\nabla z = 0\) liefert die kritischen Punkte bei \(x= \pm2\) und \(y=3\). Die Hesse-Matrix lautet \(H = \begin{pmatrix} -6x & 0 \\ 0 & 2 \end{pmatrix}\). Ihre Eigenwerte bei \((2,3)\) sind -12 und 2. Daher ist \(H\) bei \((2,3)\) indefinit und \((2,3)\) ist ein Sattelpunkt. Ihre Eigenwerte bei \((-2,3)\) sind 12 und 2. Daher ist \(H\) bei \((2,3)\) positiv definit und \((-2,3)\) ist ein lokales Minimum. Siehe Code.

3. Siehe Code.

4. Abbrechen der Taylorreihe bei \((x_0, y_0)\) nach dem quadratischen Gleid leifert allgemein \(z_{\text{quad. approx}} = z(x_0, y_0) + \text{grad}(z)^T (x_0, y_0) \begin{pmatrix} x - x_0 \\ y - y_0 \end{pmatrix} + \frac{1}{2} ( x - x_0 , y - y_0 )\, H(x_0,y_0) \begin{pmatrix} x - x_0\\ y - y_0 \end{pmatrix}\). Für \((x_0, y_0) = (-2, 3)\) erhält man \(z_{\text{quad. approx}} = -30 + 6(x + 2)^2 + (y - 3)^2\). Siehe Code.

x = arange(-4,4,.125)
y = arange(-8,8,.125)
X, Y = meshgrid(x, y)

Z = -X**3 + Y**2 + 12*X -6*Y - 5

fig = figure(figsize=(8, 4))

ax = fig.add_subplot(1, 2, 1, projection='3d')
p  = ax.plot_surface(X, Y, Z, 
                     rstride=4, cstride=4, linewidth=0, cmap=cm.PuOr)
ax.view_init(azim = -60,elev = 30)
xlabel('x')
ylabel('y')

fig.add_subplot(1, 2, 2)
CS = contour(X,Y,Z, 20, cmap= 'coolwarm_r')  # colormaps()
clabel(CS, inline=1)
xlabel('x')
ylabel('y')
grid(True)

H1 = array([[-12, 0],
              [0, 2]])
print(eig(H1)[0])

H2 = array([[12, 0],
             [0, 2]])
print(eig(H2)[0])

[-12.   2.]
[12.  2.]

x = arange(-4,4,.5)
y = arange(-8,8,.5)
X,Y = meshgrid(x, y)

Z = -X**3 + Y**2 + 12*X -6*Y - 5
U = -3*X**2 + 12
V = 2*Y - 6

figure(figsize=(5,5))
CS = contour(X,Y,Z,15, cmap= 'coolwarm_r')
Q = quiver(X,Y, U,V)
xlabel('x')
ylabel('y')
grid(True)

x = arange(-4,4,.125)
y = arange(-8,8,.125)
X, Y = meshgrid(x, y)

Z = -X**3 + Y**2 + 12*X - 6*Y - 5
Q = -30 + 6*(X + 2)**2 + (Y - 3)**2

fig = figure(figsize=(5,5))

ax = fig.add_subplot(1, 1, 1, projection='3d')
p  = ax.plot_surface(X, Y, Z, 
                     rstride=4, cstride=4, linewidth=0, cmap=cm.PuOr)
p  = ax.plot_surface(X, Y, Q, 
                     rstride=4, cstride=4, linewidth=0, cmap=cm.Greys)

ax.view_init(azim = 30,elev = 30)
xlabel('x')
ylabel('y');

x = arange(-4,4,.125)
y = arange(-8,8,.125)
X, Y = meshgrid(x, y)

Z = -X**3 + Y**2 + 12*X - 6*Y - 5
Q = -30 + 6*(X + 2)**2 + (Y - 3)**2

fig = figure(figsize=(5,5))

CS = contour(X,Y,Z, 20, cmap= 'coolwarm_r')
#clabel(CS, inline=1)
CS = contour(X,Y,Q, 20, cmap= 'coolwarm_r')
#clabel(CS, inline=1)
xlabel('x')
ylabel('y')
grid(True)

Lösung NO4: Wärmeverlustfunktion - Teil 2

Wir schreiben die Nebenbedingung als \(g(x,y,z) = xyz - 18480 = 0\). Die Optimalitätsbedingung \(\nabla Q = \lambda\nabla g\) liefert das nicht-lineares 3x3-Gleichungssystem

\[\begin{split}\begin{align} 11y + 15z &= \lambda yz \\ 11x + 14z &= \lambda xz \\ 14y + 15x &= \lambda xy. \end{align}\end{split}\]

Freistellen von \(\lambda\) in jeder Gleichung und Gleichsetzen der Terme der ersten mit der zweiten und der zweiten mit der dritten Gleichung liefert \(x=\frac{14}{15}y\) sowie \(z=\frac{11}{15}y\). Einsetzen dieser Zwischenergebnisse in die Nebenbedingung ergibt die Lösung \(x = 28, y = 30, z = 22\).

y = (18480*(15**2)/(14*11))**(1/3)
x = 14/15*y
z = 11/15*y

print("x = {:.2f}".format(x))
print("y = {:.2f}".format(y))
print("z = {:.2f}".format(z))

x = 28.00
y = 30.00
z = 22.00

Lösung NO5: Produktionsplan und Produktionsmöglichkeitenkurve

Die Zielfunktion lautet \(f(x,y)=3x+4y\), und die Nebenbedingung scheiben wir als \(g(x,y)=9x^2 + 4y^2 - 18000 = 0\). Die Optimalitätsbedingung \(\nabla f = \lambda\nabla g\) liefert ein lineares Gleichungssystem, dessen Lösung den optimalen Produktionsplan \(x = 20\), \(y = 60\) enthält. Der maximale Gewinn ist \(f(20,60)= 300\) EUR. Siehe Code

l = sqrt(5/(4*18000))
x = 1/(6*l)
y = 1/(2*l)

a = sqrt(2000)
x = linspace(0.1, a - 0.01, 100)
y = 0.5*sqrt(18000 - 9*x**2)

delta = 0.25
X, Y = meshgrid(x, y)
c = array([3, 4])
Z = c[0]*X + c[1]*Y


figure(figsize=(5,3))
plot(x, y, '-k')
CS = contour(X, Y, Z, cmap='coolwarm')
plot(20, 60,'or')
xlabel('x')
ylabel('y')
xlim(0,a+1)
grid(True)

Lösung NO6: Preisdifferenzierung

1. Die Zielfunktion (Gewinn = Erlös - Kostem) lautet \(f(x,y)= (97 - \frac{x}{10})x + (83 - \frac{y}{20})y - \left[ 20000 + 3(x + y)\right] = 94x - \frac{x^2}{10} + 80y - \frac{y^2}{20} - 20000\). Die Optimalitätsbedingung \(\nabla f = 0\) liefert ein lineares Gleichungssystem, dessen Lösung \(x=470\) und \(y=800\) den einzigen kritischen Punkt ergibt. Die Hesse-Matrix \(H=\begin{pmatrix} -\frac{1}{5} & 0 \\ 0 & -\frac{1}{10} \end{pmatrix}\) ist negativ definit. Daher ist der kritische Punkt \((x,y)=(470,800)\) ein lokales Maximum. Der zugehörige Gewinn \(f(470,800)\) hat den Wert 34090 EUR. Siehe auch Code.

2. Zur Zielfunktion \(f(x,y) = 94x - \frac{x^2}{10} + 80y - \frac{y^2}{20} - 20000\) kommt noch die Nebenbedingung \(g(x,y) = (97 - \frac{x}{10}) - (83 - \frac{y}{20}) = 0\) dazu. Die Optimalitätsbedingung \(\nabla f = \lambda\nabla g\) liefert ein lineares Gleichungssystem, dessen Lösung die optimalen Werte \(x \simeq 516.7\) und \(y \simeq 753.3\) liefert. Der zugehörige Gewinn hat den niedrigeren Wert von 33763.33 EUR. Siehe auch Code.

def gewinn(x,y):
    return (97 - x/10)*x + (83 - y/20)*y - (20000 + 3*(x + y))

print('Aufgabe 1:')
x = 470
y = 800
print(' x = {:.2f}'.format(x))
print(' y = {:.2f}'.format(y))
print(' Gewinn = {:.2f} EUR'.format(gewinn(x, y)))

print('Aufgabe 2:')
lbd = 7*40/3
x = 470 + lbd/2
y = 800 - lbd/2
print(' x = {:.2f}'.format(x))
print(' y = {:.2f}'.format(y))
print(' Gewinn = {:.2f} EUR'.format(gewinn(x, y)))

Aufgabe 1:
 x = 470.00
 y = 800.00
 Gewinn = 34090.00 EUR
Aufgabe 2:
 x = 516.67
 y = 753.33
 Gewinn = 33763.33 EUR

Lösung NO7: Energieversorgungsnetz

Die Zielfunktion lautet \(f(x_1, x_2, x_3) = f_1(x_1) + f_2(x_2) + f_3(x_3)\). Die Nebenbedingung schreiben wir als \(g(x_1, x_2, x_3) = x_1 + x_2 + x_3 - 952 = 0\). Dann liefert die Optimalitätsbedingung \(\nabla f = \lambda\nabla g\) ein lineares Gleichungssystem, dessen Lösung die optimalen Werte der \(x_i\) enthält, siehe Code.

def Kosten(x):
    return x[0] + 0.0625*x[0]**2 + x[1] + 0.0125*x[1]**2 + x[2] + 0.0250*x[2]**2

A = array([[0.125, 0, 0, -1],
           [0, 0.025, 0, -1],
           [0, 0, 0.050, -1],
           [1, 1,     1,  0]])
b = array([-1, -1, -1, 952])
x = solve(A, b)

print('x = ', x[:3])
print('lambda = ', x[3])
print('Kosten = {:.2f} EUR/Stunde'.format(Kosten(x[:3])))

x =  [112. 560. 280.]
lambda =  15.0
Kosten = 7616.00 EUR/Stunde

Bemerkung: Der Wert des Lagrange-Multiplikators (auch Schattenpreis genannt) ist die Rate, mit welcher der sich der optimale Zielfunktionswert ändert, wenn man die Randbedingungen ändert:

A = array([[0.125, 0, 0, -1],
           [0, 0.025, 0, -1],
           [0, 0, 0.050, -1],
           [1, 1,     1,  0]])
b = array([-1, -1, -1, 952 + 1]) # Achtung: 952 + 1
x = solve(A, b)
print('Kosten = {:.2f} EUR/Stunde'.format(Kosten(x[:3])))

Kosten = 7631.01 EUR/Stunde

Lösung NO8: Produktionsplan und Produktionsmöglichkeitenkurve

Maximiere \(f(x,y) = 2x + 10y\) unter \(g(x,y) = 4x^2 + 25y^2 - 50000 = 0\). Die Methode der Lagrange-Multiplikatoren liefert die optimalen Werte \(x\)=50 und \(y\)=40.

Lösung NO9: Design eines Schwimmbeckens

Länge \(x\), Breite \(y\), Höhe/Tiefe \(z\). Maximiere \(f(x,y) = xy + 2xz + 2yz\) unter \(g(x,y) = xyz - 108 = 0\). Die Methode der Lagrange-Multiplikatoren liefert die optimalen Werte \(x=y=2z=6\).

Siehe Lothar Papula: Klausur- und Übungsaufgaben. Auflage 4, Aufgabe E71.

Lösung N1O: Extrema

Optimalitätsbedingung \(\nabla f =0\) liefert einen kritischen Punkt mit \(x = 2/7\) und \(y=8/7\). Die Hessematrix von \(f\) ist dort positiv definit, sodass dort ein Minimum vorliegt.

Siehe Sanal: Mathematik für Ingenieure. p. 583, Bsp. 11.61

Kurztestfragen

1. Wozu braucht man die Hessematrix, und wie berechnet man sie?

2. Was ist ein kritischer Punkt?

3. Unter welchen Bedingungen, können Sie sich sicher sein, ein lokales Minimum einer mehrdimensionalen Funktion gefunden zu haben?

4. Unter welchen Bedingungen, können Sie sich sicher sein, ein lokales Maximum einer mehrdimensionalen Funktion gefunden zu haben?

5. Bei einem kritischen Punkt ist die Hessematrix negativ definit. Was können Sie daraus (nicht) schließen?

6. Finden Sie den kritischen Punkt der Funktion \(f(x,y) = -x^2 - 2y^2 + 4x + 2y + 8\).

7. Für die Funktion des obigen Bsp. 6, berechnen Sie die Hesse Matrix. Was sagt diese Matrix bezüglich einem Maximum oder Minimum der Funktion aus?

8. Finden Sie den kritischen Punkt der Funktion \(f(x,y) = 2x^2 + y^2 + 8x - 6y + 20\).

9. Für die Funktion des obigen Bsp. 8, berechnen Sie die Hesse Matrix. Was sagt diese Matrix bezüglich einem Maximum oder Minimum der Funktion aus?

10. Unter welchen Bedingungen können Sie sich sicher sein, ein lokales Maximum einer mehrdimensionalen Funktion gefunden zu haben?

11. Berechnen Sie alle Extrempunkte der Funktion \(f(x,y)=64x^2-64x+4y^3-48y-4\).

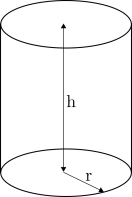
12. Die Wärmeverluste eines zylindrischen Warmwasserspeichers sollen minimiert werden. Über die Mantelfläche gehen \(40~\mathrm{W/m^2}\) verloren und über die Deck- und die Grundfläche jeweils \(20~\mathrm{W/m^2}\). Der Warmwasserspeicher besitzt ein Volumen von \(\pi~\mathrm{m^3}\). Wie sind Radius und Höhe zu wählen, um den Wärmeverlust zu minimieren? Gehen Sie dazu vor wie folgt:

    1. Geben Sie den Wärmeverlust \(\dot{Q}\) als Funktion von Radius und Höhe an.

    2. Berechnen Sie den Gradienten dieser Funktion und der Nebenbedingung \(g\).

    3. Berechnen Sie das Optimum, welches sich durch die Bedingung \(\nabla \dot{Q}=\lambda \nabla g\) ergibt.

    

Programmierprojekte

Portfoliooptimierung

Literatur:

• Empfehlung: David G. Luenberger: Investment Science. Oxford University Press, 2nd edition, 2013. Chapter 6 Mean-Variance Portfolio Theory. Fünf Exemplare stehen in der FHV-Bibliothek.

• Harry M. Markowitz: Er wurde 1990 für seine Theorie der Portfolio-Auswahl mit dem Wirtschaftsnobelpreis zusammen mit Merton H. Miller und William F. Sharpe ausgezeichnet.

Theorie:

Die (einfache) Rendite eines Assets (Finanzprodukt, Geld- oder Kapitalanlage, z. B. Sparbuch mit variablen Zinsen, Anleihe, Aktie, Option) über einen Zeitraum (=Periode, z. B. Tag, Monat, Jahr) von \(t_1\) bis \(t_2\) ist definiert als das Verhältnis

\[r = \frac{X(t_2) - X(t_1)}{X(t_1)},\]

wobei \(X(t)\) den Wert (z. B. in EUR) des Assets zum Zeitpunkt \(t\) bezeichnet. Es folgt

\[X(t_2) = X(t_1)(1 + r).\]

Beispiel: Aktie mit Rendite \(r=0.07\) und Anfangswert \(X(t_1) = 200\) EUR. Der Wert am Ende des betrachteten Zeitraums berechnet sich zu \(X(t_2) = 200\,(1 + 0.07) = 214\) EUR.

Beobachtet man die Renditewerte eines Assets über mehrere Zeitäume, so erhält man eine Zeitreihe von Renditewerten, die einen bestimmten Mittelwert \(\mu\) und eine bestimmte Standardabweichung \(\sigma\) bzw. Varianz \(\sigma^2\) hat.

In einem Portfolio wird das zur Verfügung stehende Gesamtkapital in mehrere Assets gewichtet aufgeteilt. Wir betrachten den Fall von zwei Assets mit Mittelwerten \(\mu_1\) und \(\mu_2\) sowie Standardabweichungen \(\sigma_1\) und \(\sigma_1\) der jeweiligen Renditen. Wir gewichten das erste Asset mit \(0 \leq w_1 \leq 1\) und das zweite Asset mit \(0 \leq w_1 \leq 1\). Die beiden Gewichte addieren sich zu eins: \(w_1 + w_2 =1\). Achtung: Um die Gewichtung der beiden Assets im Portfolio über mehrere Perioden konstant bei den gewählten Werten \(w_1\) und \(w_2\) zu halten, ist es im Allgemeinen notwendig, nach jeder Periode zwischen den Assets umzuschichten.

Das Portfolio bildet ein neues Asset (oft auch Fond genannt, engl. Fund), dessen Renidte wiederum einen Mittelwert \(\mu_P\) und eine Standardabweichung \(\sigma_P\) besitzt. Diese lassen sich mit folgenden Formeln bestimmen:

\[\begin{split}\begin{align} \mu_P & = w_1 \mu_1 + w_2 \mu_2 = (\mu_1, \mu_2) \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} \\ \sigma_P^2 & = (w_1, w_2) \begin{pmatrix} \sigma_1^2 & \rho\sigma_1\sigma_2 \\ \rho\sigma_1\sigma_2 & \sigma_2^2\end{pmatrix} \begin{pmatrix} w_1 \\ w_2 \end{pmatrix} \end{align}\end{split}\]

Die 2x2-Matrix ist die Kovarianzmatrix der Einzelrenditen. Sie wird meist mit \(\Sigma\) abgekürzt und enthält die Korrelation \(-1 \leq \rho \leq 1\) der Einzelrenditen. Der Mittelwert \(\mu_P\) der Portfoliorentdite ist eine lineare Funktion der Gewichte \(w_1\) und \(w_2\), die Standardabweichung \(\sigma_P\) der Portfoliorentdite ist keine lineare Funktion der Gewichte \(w_1\) und \(w_2\).

Wir schreiben nun alles in Vektor/Matrix-Notation, die auch die Verallgemeinerung auf mehr als zwei Assets umfasst:

\[\begin{split}\begin{align} \mu_P & = \mu^T w \\ \sigma_P^2 & = w^T \Sigma w \end{align}\end{split}\]

In einem Portfolio wird durch geschickte Wahl der Gewichte das “Risiko”, das mit der Standardabweichung der Portfolirendite (oder äquivalent mit deren Quadrat der Varianz) gemessen wird, möglichst klein und der “Gewinn”, der mit dem Mittelwert der Portfolirendite gemessen wird, möglichst groß oder konstant gehalten. Folgende Optimierungsprobleme werden in der klassischen Portfoliotheorie daher behandelt:

Finde jenen Gewichtungsvektor \(w\) mit

(A) min. \(\sigma_P^2(w)\) s. t. \(1^T w = 1\), oder

(B) min. \(\sigma_P^2(w)\) s. t. \(1^T w = 1\) und \(\mu_P(w) = \mu_0\) für einen vorgegebenen Wert \(\mu_0\)

In der Bedingung \(1^T w = 1\) bezeichnet \(1^T\) den Zeilenvektor mit lauter Einsern und 1 die Zahl Eins.

Software zum Arbeiten mit historischen Daten:

• Pandas: Installation im Anaconda Command-Prompt mit conda install pandas

• Pandas-Datareader: Installation im Anaconda Command-Prompt mit conda install pandas-datareader

Abgabe: Hochladen eines IPython-Notebooks als ipynb-Datei in ILIAS.

import pandas as pd

if False:
    from pandas.plotting import register_matplotlib_converters
    register_matplotlib_converters()

    import pandas_datareader as pdr

    # Tickersymbole siehe: https://www.google.com/finance
    A1 = pdr.get_data_yahoo("AAPL" , start='2006-01-02', end='2016-11-11')
    A2 = pdr.get_data_yahoo("GOOGL", start='2006-01-02', end='2016-11-11')
    
    A1.to_csv('daten/A1.csv')
    A2.to_csv('daten/A2.csv')

# for offline use save data to disk and later load data:
if True:
    A1 = pd.read_csv('daten/A1.csv', index_col=0, parse_dates=[0])
    A2 = pd.read_csv('daten/A2.csv', index_col=0, parse_dates=[0])

# zeitlicher Verlauf der Schlusskurse:
figure(figsize=(6,4))
plot(A1.Close, label='Asset 1')
plot(A2.Close, label='Asset 2')
xlabel('Zeit')
ylabel('Wert')
legend(loc='best');

# Renditen für Periode = 250 Handelstage, entspricht ca. einem Jahr:
r1 = A1.Close.pct_change(250).dropna()
r2 = A2.Close.pct_change(250).dropna()

# Dataframe der Renditen
df = pd.DataFrame({'A1':r1,
                   'A2':r2})
print(df.head(),'\n')

print('Mittelwerte:\n',          df.mean(),'\n', sep='')
print('Standardabweichungen:\n', df.std() ,'\n', sep='')
print('Kovarianzmatrix:\n',      df.cov() ,'\n', sep='')
print('Korrelationsmatrix:\n',   df.corr(),'\n', sep='')

                  A1        A2
Date                          
2006-12-29  0.134983  0.058015
2007-01-03  0.117780  0.050198
2007-01-04  0.151654  0.070960
2007-01-05  0.114679  0.046235
2007-01-08  0.123866  0.035725 

Mittelwerte:
A1    0.346793
A2    0.174777
dtype: float64

Standardabweichungen:
A1    0.453369
A2    0.267702
dtype: float64

Kovarianzmatrix:
          A1        A2
A1  0.205544  0.049163
A2  0.049163  0.071665

Korrelationsmatrix:
         A1       A2
A1  1.00000  0.40507
A2  0.40507  1.00000

# als arrays:
mu = df.mean().values
s  = df.std().values
S  = df.cov().values

Aufgaben:

• Zeichnen Sie das \(\mu\)-\(\sigma\)-Diagramm für zwei Assets bei unterschiedlichen Korrelationswerten: Wählen Sie zuerst für zwei Assets sinnvolle Mittelwerte \(\mu_1\) und \(\mu_2\) sowie Standardabweichungen \(\sigma_1\) und \(\sigma_1\). Zeichnen Sie nun in der \(\mu\)-\(\sigma\)-Ebene für unterschiedliche Korrelationswerte \(\rho\) jeweils die Kurve der zugehörigen Portfolios als Punkt \((\sigma_P, \mu_P)\), indem Sie die Gewichtung variieren.

• Zeigen Sie für den allgemeinen Fall von \(n\) Assets, dass die Optimerungsprobleme (A) und (B) durch die folgenden linearen Gleichungssysteme gelöst werden:

  (A) \(\begin{pmatrix} 2\Sigma & -1 \\ 1^T & 0\end{pmatrix} \begin{pmatrix} w \\ \lambda \end{pmatrix} = \begin{pmatrix}0 \\ 1 \end{pmatrix}\)
  (B) \(\begin{pmatrix} 2\Sigma & -\mu & -1 \\ \mu^T & 0 & 0 \\ 1^T & 0 & 0\end{pmatrix} \begin{pmatrix} w \\ \lambda \\ \nu \end{pmatrix} = \begin{pmatrix}0 \\ \mu_0 \\ 1 \end{pmatrix}\)

• Verwenden Sie historische Daten von 5 unterschiedlichen Assets und

  1. lösen Sie das Optimerungsproblem (A),

  2. lösen Sie das Optimierungsproblem (B) für unterschiedliche \(\mu_0\)-Werte, und

  3. stellen Sie Ihre Ergebnisse in der \(\mu\)-\(\sigma\)-Ebene dar.

Abgabe: Hochladen eines Ipython-Notebook als ipynb-Datein und aller evtl. zusätzlichen (Daten-)Files in ILIAS. Benennung der Files: Nachname_Vorname_Dateibeschreibung.*

Lösungen:

Zeichnen Sie das \(\mu\)-\(\sigma\)-Diagramm für zwei Assets bei unterschiedlichen Korrelationswerten: Wählen Sie zuerst für zwei Assets sinnvolle Mittelwerte \(\mu_1\) und \(\mu_2\) sowie Standardabweichungen \(\sigma_1\) und \(\sigma_1\). Zeichnen Sie nun in der \(\mu\)-\(\sigma\)-Ebene für unterschiedliche Korrelationswerte \(\rho\) jeweils die Kurve der zugehörigen Portfolios als Punkt \((\sigma_P, \mu_P)\), indem Sie die Gewichtung variieren.

m1 = 0.02   # Mittelwert Rendite Asset 1
m2 = 0.05   # Mittelwert Rendite Asset 2
s1 = 0.02   # Standardabweichung Rendite Asset 1
s2 = 0.03   # Standardabweichung Rendite Asset 2

# Korrelation der Renditen
rho = -.5    

# Kovarianzmatrix der Renditen
S = array([[s1**2, rho*s1*s2],
           [rho*s1*s2, s2**2]]) 
print(S)

[[ 0.0004 -0.0003]
 [-0.0003  0.0009]]

# Gewichtungen des Assets 1:
weights1 = linspace(0, 1, num = 50)

figure(figsize=(4,4))

for w1 in weights1:
    w = array([w1, 1 - w1])   # Vektor der Assetsgewichte
    m = w1*m1 + (1 - w1)*m2   # Mittelwert Rendite Portfolio
    s = sqrt(w@S@w)           # Standardabweichung Rendite Portfolio
    plot(s, m, 'or') 
    
plot(s1, m1, 'om', label='Asset 1') 
plot(s2, m2, 'ob', label='Asset 2')

xlabel('Std. der Rendite (Risiko)')
ylabel('Mittlere Rendite (Gewinn)')
legend(loc= 'best', numpoints = 1)
xlim(0, 0.035)
ylim(0, 0.055)
grid(True)

interaktive Version mit Wahl der Korrelation:

from ipywidgets import interact

weights1 = linspace(0, 1, num = 30)

def fun(rho):
    S = array([[s1**2, rho*s1*s2],
               [rho*s1*s2, s2**2]])
    figure(figsize=(4,4))
    for w1 in weights1:
        w = array([w1, 1 - w1])   # Vektor der Assetsgewichte
        m = w1*m1 + (1 - w1)*m2
        # s = sqrt(dot(dot(w,S),w))
        s = sqrt(w@S@w)
        plot(s, m, 'or') 
    
    plot(s1, m1, 'om', label='Asset 1') 
    plot(s2, m2, 'ob', label='Asset 2')
    xlabel('Std. der Rendite (Risiko)')
    ylabel('Mittlere Rendite (Gewinn)')
    legend(loc= 'best', numpoints = 1)
    xlim(0, 0.035)
    ylim(0, 0.055)
    grid(True)
    show()

interact(fun, rho=(-1, 1, 0.1)); 

Zeigen Sie für den allgemeinen Fall von \(n\) Assets, dass die Optimerungsprobleme (A) und (B) durch die folgenden linearen Gleichungssysteme gelöst werden:

(A) \(\begin{pmatrix} 2\Sigma & -1 \\ 1^T & 0\end{pmatrix} \begin{pmatrix} w \\ \lambda \end{pmatrix} = \begin{pmatrix}0 \\ 1 \end{pmatrix}\)
(B) \(\begin{pmatrix} 2\Sigma & -\mu & -1 \\ \mu^T & 0 & 0 \\ 1^T & 0 & 0\end{pmatrix} \begin{pmatrix} w \\ \lambda \\ \nu \end{pmatrix} = \begin{pmatrix}0 \\ \mu_0 \\ 1 \end{pmatrix}\)

Lösung via Lagrange-Multiplikatoren:

Der Gradient von \(w^T \Sigma w\) bzgl. \(w\) ist \(2\Sigma w\), was sich z. B. im 2-dimesionalen Fall überprüfen läßt. Der Gradient von \(1^T w\) bzgl. \(w\) ist \(1\), der Gradient von \(\mu^T w\) bzgl. \(w\) ist \(\mu\). Somit lauten die Optimalitätskriterien

(A) \(2\Sigma w = \lambda 1\) und \(1^T w = 1\)

(B) \(2\Sigma w = \lambda \mu + \nu 1\), \(\mu^T w = \mu_0\) und \(1^T w = 1\)

Bring man diese Gleichungen in Blockmatrixform, erhält man das angegebene Ergebnis.

Verwenden Sie historische Daten von 5 unterschiedlichen Assets und

1. lösen Sie das Optimerungsproblem (A),

2. lösen Sie das Optimierungsproblem (B) für unterschiedliche \(\mu_0\)-Werte, und

3. stellen Sie Ihre Ergebnisse in der \(\mu\)-\(\sigma\)-Ebene dar.

if False:
    A1 = pdr.get_data_yahoo("AAPL" , start='2006-01-02', end='2016-11-11')
    A2 = pdr.get_data_yahoo("GOOGL", start='2006-01-02', end='2016-11-11')
    A3 = pdr.get_data_yahoo("AMZ"  , start='2006-01-02', end='2016-11-11')
    A4 = pdr.get_data_yahoo("ORCL" , start='2006-01-02', end='2016-11-11')
    A5 = pdr.get_data_yahoo("MSFT" , start='2006-01-02', end='2016-11-11')
    
    A1.to_csv('daten/AAPL.csv')
    A2.to_csv('daten/GOOGL.csv')
    A3.to_csv('daten/AMZ.csv')
    A4.to_csv('daten/ORCL.csv')
    A5.to_csv('daten/MSFT.csv')

# for offline use save data to disk and later load data:
if True:
    A1 = pd.read_csv('daten/AAPL.csv', index_col=0, parse_dates=[0])
    A2 = pd.read_csv('daten/GOOGL.csv', index_col=0, parse_dates=[0])
    A3 = pd.read_csv('daten/AMZ.csv', index_col=0, parse_dates=[0])
    A4 = pd.read_csv('daten/ORCL.csv', index_col=0, parse_dates=[0])
    A5 = pd.read_csv('daten/MSFT.csv', index_col=0, parse_dates=[0])

r1 = A1.Close.pct_change(250).dropna()
r2 = A2.Close.pct_change(250).dropna()
r3 = A3.Close.pct_change(250).dropna()
r4 = A4.Close.pct_change(250).dropna()
r5 = A5.Close.pct_change(250).dropna()

df = pd.DataFrame({'A1':r1,
                   'A2':r2,
                   'A3':r3,
                   'A4':r4,
                   'A5':r5
                  })
mu = df.mean().values
s  = df.std() .values
S  = df.cov() .values

print(df.head())

                  A1        A2  A3        A4        A5
Date                                                  
2006-12-29  0.134983  0.058015 NaN  0.360317  0.112519
2007-01-03  0.117780  0.050198 NaN  0.387480  0.107156
2007-01-04  0.151654  0.070960 NaN  0.382330  0.104483
2007-01-05  0.114679  0.046235 NaN  0.344512  0.101449
2007-01-08  0.123866  0.035725 NaN  0.386646  0.114296

figure(figsize=(4,4))
plot(s, mu, 'or', label='assets')
xlim(0, 0.5)
ylim(0, 0.4)
xlabel('Std. der Rendite (Risiko)')
ylabel('Mittlere Rendite (Gewinn)')
grid(True)

Optimerungsproblem (A):

n  = len(mu)  # Anzahl Assets
es = ones(n)

A_mv = zeros((n+1,n+1))
A_mv[:n,:n] = 2*S
A_mv[:n,n]  = -es
A_mv[n,:n]  =  es
print(array_str(A_mv, precision=2, suppress_small=True))

b_mv    = zeros(n + 1)
b_mv[n] = 1
print(b_mv)

[[ 0.41  0.1   0.02  0.09  0.1  -1.  ]
 [ 0.1   0.14  0.03  0.04  0.09 -1.  ]
 [ 0.02  0.03  0.44  0.01  0.   -1.  ]
 [ 0.09  0.04  0.01  0.07  0.03 -1.  ]
 [ 0.1   0.09  0.    0.03  0.1  -1.  ]
 [ 1.    1.    1.    1.    1.    0.  ]]
[0. 0. 0. 0. 0. 1.]

w_mv = solve(A_mv, b_mv)[:n]
ptf_mv_mu = dot(mu, w_mv)
ptf_mv_s  = sqrt(dot(dot(w_mv,S),w_mv))

figure(figsize=(4,4))
plot(s, mu, 'or', label='assets')
plot(ptf_mv_s, ptf_mv_mu, 'hb', label='min. var. portfolio')
xlim(0, 0.5)
ylim(0, 0.4)
xlabel('Std. der Rendite (Risiko)')
ylabel('Mittlere Rendite (Gewinn)')
legend(loc='best', numpoints=1)
grid(True)

Optimierungsproblem (B) für einen \(\mu_0\)-Wert:

mu0 = 0.20

A   = zeros((n+2,n+2))
A[:n,:n]  =  S
A[:n,n]   = -mu
A[:n,n+1] = -es
A[n,:n]   =  mu
A[n+1,:n] =  es

print(array_str(A, precision=2, suppress_small=True))

[[ 0.21  0.05  0.01  0.05  0.05 -0.35 -1.  ]
 [ 0.05  0.07  0.01  0.02  0.04 -0.17 -1.  ]
 [ 0.01  0.01  0.22  0.    0.   -0.52 -1.  ]
 [ 0.05  0.02  0.    0.03  0.02 -0.12 -1.  ]
 [ 0.05  0.04  0.    0.02  0.05 -0.1  -1.  ]
 [ 0.35  0.17  0.52  0.12  0.1   0.    0.  ]
 [ 1.    1.    1.    1.    1.    0.    0.  ]]

b      = zeros(n+2)
b[n]   = mu0
b[n+1] = 1

print(b)

[0.  0.  0.  0.  0.  0.2 1. ]

w = solve(A,b)[:n]
print(w)

[-1.16352803e-02  2.68717045e-05  2.24243884e-01  5.31631823e-01
  2.55732701e-01]

ptf_mu = dot(mu, w)
print(ptf_mu)

ptf_s = sqrt(dot(dot(w,S),w))
print(ptf_s)

0.19999999999999998
0.16657058020706295

figure(figsize=(4,4))
plot(s, mu, 'or', label='assets')
plot(ptf_s, ptf_mu, 'ob', label='portfolio')
xlim(0, 0.5)
ylim(0, 0.5)
xlabel('Std. der Rendite (Risiko)')
ylabel('Mittlere Rendite (Gewinn)')
legend(loc='best', numpoints=1)
grid(True)

Optimierungsproblem (B) für unterschiedliche \(\mu_0\)-Werte:

figure(figsize=(4,4))
plot(s, mu, 'or', label='assets')
for m0 in linspace(0, 0.4, 20):
    b[n]   = m0
    w      = solve(A,b)[:n]
    ptf_mu = dot(mu, w)
    ptf_s  = sqrt(dot(dot(w,S),w))
    plot(ptf_s, ptf_mu, 'hy')
plot(ptf_mv_s, ptf_mv_mu, 'hb', label='min. var. portfolio')
xlim(0, 0.5)
ylim(0, 0.5)
xlabel('Std. der Rendite (Risiko)')
ylabel('Mittlere Rendite (Gewinn)')
legend(loc='best', numpoints=1)
grid(True)

Numerische Lösung nicht-linearer Optimierungsprobleme

Wir wollen numerisch das/ein/die Minimum/Minima der nicht-linearen Funktion \(f(x,y) = (0.02 x^2 + y^2)^{0.9}\) bestimmen. Aus der Funktionsgleichung (dieses absichtlich so gewählten Beispiels) ist ersichtlich, dass es nur ein Minimum gibt und dieses bei \(p^*=(0,0)\) liegt. Im allgemeinen Fall gibt die Funktionsgleichung aber keinen Aufschluss darüber oder es gibt gar keine Funktionsgleichung, wenn Funktionswerte nur durch Evaluation einer black box berechnet werden können.

Sie sollen anhand folgender Aufgaben untersuchen, ob der Ansatz “Folge dem negativen Gradienten” zum Ziel führt:

1. Begründen Sie den Ansatz “Folge dem negativen Gradienten”.

2. Erstellen Sie einen Kontourplot der Funktion, und plotten Sie zusätzlich das Gradientenfeld der Funktion in die Abbildung. Verwenden Sie den Bereich \(x\in [-10, 10]\) und \(y\in [-5, 5]\).

3. Berechnen Sie ausgehend vom Startpunkt \(p_0 = (-8, -4)\) iterativ 100 Folgepunkte in der \(x\)-\(y\)-Ebene mittels der Rekursion

   \[p_{i+1} = p_i - \nabla f(p_i).\]

   Fügen Sie die Punkte in den Kontourplot ein. Interpretieren Sie das Ergebnis.

4. Beschreiben Sie, wie Sie den Ansatz verbessern würden, und beschreiben Sie ein sinnvolles Abbruchkriterium.

Abgabe: Hochladen eines IPython-Notebooks als ipynb-Datei in ILIAS.

Lösung:

Link: Wikipedia: Gradient_descent

x = linspace(-10, 10, 200)
y = linspace( -5,  5, 200)
X, Y = meshgrid(x, y)
E = 0.9    # Exponent
Z = (0.02*X**2 + Y**2)**E

fig = figure(figsize=(8,4))

cs = contour(X, Y, Z, 30, cmap= 'coolwarm');

x = linspace(-10, 10, 20)
y = linspace( -5,  5, 20)
X, Y = meshgrid(x, y)
Gx = E*(0.02*X**2 + Y**2)**(E - 1) * 0.04*X
Gy = E*(0.02*X**2 + Y**2)**(E - 1) * 2*Y
Q = quiver(X, Y, Gx, Gy, scale=15)

xlabel('x')
ylabel('y')
axis('equal')
grid(False)

p0 = array([-8, -4])  # Startpunkt
N = 101
P = zeros((2, N))
P[:,0] = p0
def my_grad(p):
    x = p[0]
    y = p[1]
    gx = E*(0.02*x**2 + y**2)**(E - 1) * 0.04*x
    gy = E*(0.02*x**2 + y**2)**(E - 1) * 2*y
    g = array([gx, gy])
    return g

for i in range(N-1):
    P[:,i+1] = P[:,i] - my_grad(P[:,i])

x = linspace(-10, 10, 200)
y = linspace( -5,  5, 200)
X, Y = meshgrid(x, y)
Z = (0.02*X**2 + Y**2)**E

fig = figure(figsize=(10,5))
cs = contour(X, Y, Z, 50, cmap= 'coolwarm');
plot(P[0,:], P[1,:],'.-k', alpha=0.5)
xlabel('x')
ylabel('y')
axis('equal')
grid(True)

previous

Nicht-lineare Optimierung - Vorlesung

next

Mehrdimensionale Funktionen - Vorlesung