Code
import numpy as np
import matplotlib.pyplot as plt
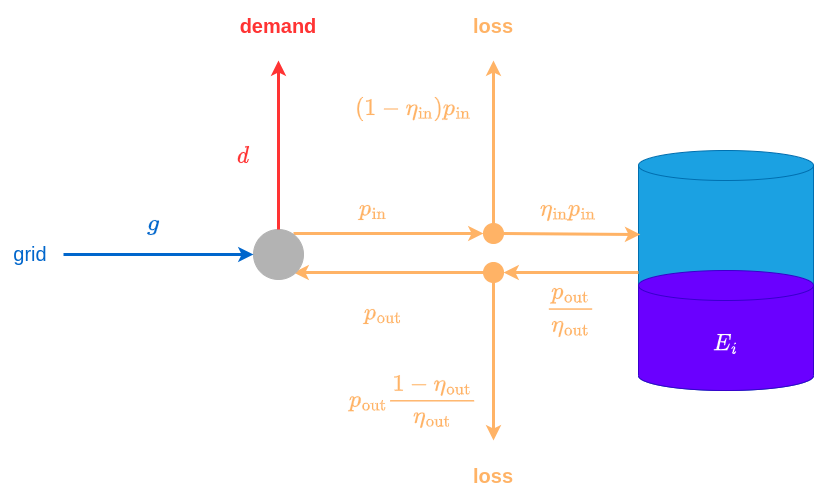
import pyomo.environ as pyoReale Batterien haben oft nicht zu vernachlässigende Lade- und Entladeverluste. Wir modellieren im Folgenden eine Batterie mit 90 % Ladewirkungsgrad und 90 % Entladewirkungsgrad. Die Batterie habe eine Kapazität von 50 kWh und maximal 20 kW Lade- und Entladeleistung. Die Batterie sei zu Beginn und am Ende zu 50 % geladen.
Wir betrachten einen Zeitraum von 8 Stunden in Viertelstundenschritten und verwenden die Batterie, um bei gegebenem Lastprofil und gegebenen zeitabhängigen Energiepreisen
Wir modellieren und implementieren beide Optimierungsprobleme und untersuchen folgende Frage: Wann führt eine Relaxierung des MILP- zu einem LP-Optimierungsproblems ebenfalls zu einer optimalen Lösung?
# data:
dt = 0.25 # h
times = np.arange(start=0, stop=8 + dt, step=dt)
periods = np.arange(start=0, stop=8, step=dt)
np.random.seed(10)
noise = np.random.normal(loc=0, scale=0.5, size=len(periods))
demand = 2 + 0.2*periods - 0.1*(periods - 4)**2 + noise
# case: use peak power objective, the following extra demand entry, gurobi and relax=True
# demand[15] = 100
price = 0.15 + 0.002*(periods - 4)**3
plt.figure(figsize=(5, 4))
plt.subplot(2, 1, 1)
plt.step(periods, demand, where='post', color='black', marker='.')
plt.xlabel('time (h)')
plt.ylabel('demand (kW)')
plt.grid()
plt.subplot(2, 1, 2)
plt.step(periods, price, where='post', color='r', marker='.')
plt.xlabel('time (h)')
plt.ylabel('price (EUR/kWh)')
plt.grid()
plt.tight_layout()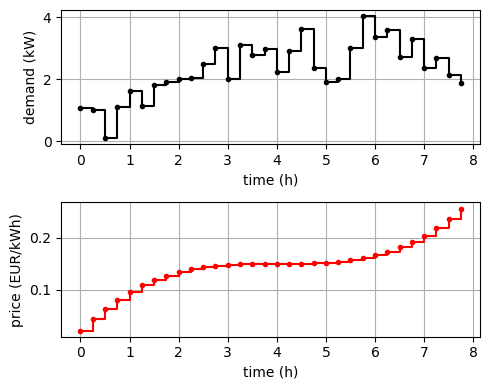
Daten:
Entscheidungsvariablen:
Zielfunktionen:
Nebenbedingungen:
Die Energie der Batterie zu Beginn: \(E_0 = E_\text{start}\)
Die Energie der Batterie am Ende: \(E_n = E_\text{end}\)
zeitliche Änderung der Energie der Batterie: \[E_{i+1} = E_i + (\eta_\text{in} p_{\text{in},i} - \frac{p_{\text{out},i}}{\eta_\text{out}}) \Delta t \quad \forall i = 0, 1, 2, \ldots, n-1\]
Kein gleichzeitiges Laden und Entladen der Batterie:
Netzwerkgleichungen: \[g_j + p_{\text{out},j} = d_j + p_{\text{in},j} \quad \forall j = 0, 1, 2, \ldots, n-1\]
n = len(periods)
time_indices = range(n + 1) # 0, 1, ..., n - 1, n
period_indices = range(n) # 0, 1, ..., n - 1
eta_in = 0.9 # efficiency of charging
eta_out = 0.9 # efficiency of discharging
E_max = 50.0 # kWh, maximum energy level
E_start = 25.0 # kWh, starting energy level
E_end = 25.0 # kWh, final energy level
p_max = 20.0 # kW, maximum (dis-)charging power
objective = "cost"
objective = "peak power"
relax = False
# relax = Truemodel = pyo.ConcreteModel()
model.I = pyo.Set(initialize=time_indices)
model.J = pyo.Set(initialize=period_indices)
model.E = pyo.Var(model.I, bounds=(0.0, E_max))
model.p_in = pyo.Var(model.J, bounds=(0.0, p_max))
model.p_out = pyo.Var(model.J, bounds=(0.0, p_max))
model.g = pyo.Var(model.J, domain=pyo.Reals)
if not relax:
model.b_in = pyo.Var(model.J, domain=pyo.Binary)
model.b_out = pyo.Var(model.J, domain=pyo.Binary)
if objective == "cost":
model.obj = pyo.Objective(expr=
sum(price[j]*model.g[j]*dt for j in model.J),
sense=pyo.minimize)
elif objective == "peak power":
model.m = pyo.Var(domain=pyo.NonNegativeReals)
model.obj = pyo.Objective(expr=model.m, sense=pyo.minimize)
@model.Constraint(model.J)
def peak_power(model, j):
return model.g[j] <= model.m
@model.Constraint(model.J)
def node(model, j):
return model.g[j] + model.p_out[j] == model.p_in[j] + demand[j]
model.initial_energy = pyo.Constraint(expr = model.E[0] == E_start)
model.final_energy = pyo.Constraint(expr = model.E[n] == E_end)
@model.Constraint(model.I)
def energy_update(model, i):
if i < n:
return model.E[i + 1] == model.E[i] + (eta_in*model.p_in[i] -
model.p_out[i]/eta_out)*dt
else:
return pyo.Constraint.Skip
if not relax:
@model.Constraint(model.J)
def charging(model, j):
return model.p_in[j] <= model.b_in[j]*p_max
@model.Constraint(model.J)
def discharging(model, j):
return model.p_out[j] <= model.b_out[j]*p_max
@model.Constraint(model.J)
def only_one(model, j):
return model.b_in[j] + model.b_out[j] <= 1solver = pyo.SolverFactory('cbc')
# solver = pyo.SolverFactory('glpk')
# solver = pyo.SolverFactory('appsi_highs')
# solver = pyo.SolverFactory('gurobi')
results = solver.solve(model, tee=False)
print(f"status = {results.solver.status}")
if objective == "cost":
print(f"minimal cost = {pyo.value(model.obj):.2f} EUR")
elif objective == "peak power":
print(f"minimal peak power = {pyo.value(model.obj):.2f} kW")status = ok
minimal peak power = 2.39 kWE_sol_dict = model.E.extract_values()
E_sol = np.array([E_sol_dict[i] for i in time_indices])
g_sol_dict = model.g.extract_values()
g_sol = np.array([g_sol_dict[j] for j in period_indices])
p_in_sol_dict = model.p_in.extract_values()
p_in_sol = np.array([p_in_sol_dict[j] for j in period_indices])
p_out_sol_dict = model.p_out.extract_values()
p_out_sol = np.array([p_out_sol_dict[j] for j in period_indices])
# non concurrent (dis-)charging check: if the sum of the products
# of p_in_sol and p_out_sol is zero, then there is no time period
# where both are positive.
check = np.sum(p_in_sol*p_out_sol)
print(f"non concurrent (dis-)charging check: {check:.6f}")
plt.figure(figsize=(5, 6))
plt.subplot(2, 1, 1)
plt.step(periods, demand, where='post', color='grey', label='demand')
plt.step(periods, g_sol, where='post', color='green', label='grid')
plt.step(periods, p_in_sol, where='post', color='b', label='charging')
plt.step(periods, -p_out_sol, where='post', color='r', label='discharging')
plt.xlabel('time (h)')
plt.ylabel('power (kW)')
plt.legend()
plt.grid()
plt.subplot(2, 1, 2)
plt.plot(times, E_sol, color='black')
plt.xlabel('time (h)')
plt.ylabel('energy (kWh)')
plt.grid()
plt.tight_layout()non concurrent (dis-)charging check: 0.000000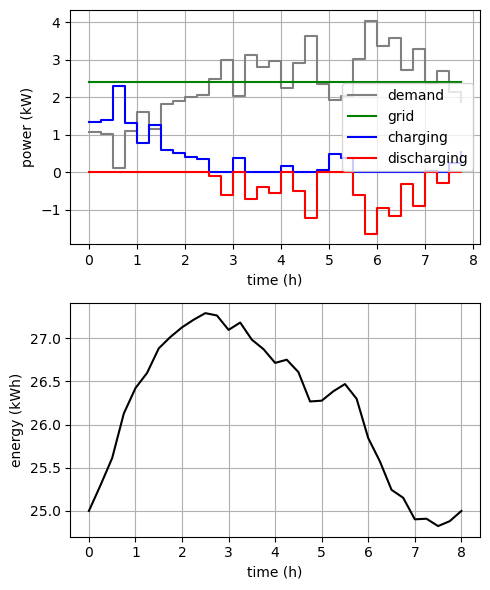
Antwort zur Frage “Wann führt eine Relaxierung des MILP- zu einem LP-Optimierungsproblems ebenfalls zu einer optimalen Lösung?”: Bei der Minimierung der Energiekosten, aber nicht immer bei der Minimierung der Spitzenlast, siehe # case: [...] im Abschnitt Daten.