Laden eines E-Mobils

Problemstellung

Sie kommen mittags um 12 Uhr mit ihrem E-Mobil nach Hause und haben nun 8 Stunden Zeit, es wieder voll zu laden, da Sie abends um 20 Uhr eine längere Reise beginnen. Ihr E-Mobil hat eine Batterie mit einer Kapazität von 60 kWh, der aktuelle SoC (State of Charge) beträgt 40 %. Ihre Ladestation hat eine maximale Ladeleistung von 11 kW. Ihr Energieversorger bietet Ihnen einen zeitabhängigen Stromtarif mit den folgenden, stündlichen Energiepreisen in Cent/kWh für die kommenden acht Stunden an: 10, 8, 12, 13, 11, 10, 13, 14.

Fragen: Mit welchen, stündlich konstanten Ladeleistungen \(p_j\) sollen Sie Ihr E-Mobil laden, so dass Sie die Ladekosten minimieren? Wie hoch sind die minimalen Ladekosten? Wann ist Ihr E-Mobil voll geladen?

Vorgehen:

  1. Definieren Sie die Zeitpunkte, Zeitperioden und ihre Indizierung.
  2. Erstellen Sie einen Plot der Energiepreise über die acht Stunden.
  3. Modellieren Sie das Energienetzwerk und fixieren Sie die Pfeilrichtung der Kanten.
  4. Basierend auf dieser Vorzeichenkonvention formulieren Sie das Optimierungsproblem:
    1. Definieren Sie die Entscheidungsvariablen inklusive Einheiten, Datentyp und Schranken.
    2. Formulieren Sie die Zielfunktion.
    3. Formulieren Sie die die Nebenbedingungen.
  5. Modellieren Sie das LP mit Pyomo. Warum ist es sinnvoll, die Entscheidungsvariablen mit Indizes \(0, 1, 2, \ldots\) anstatt mit Zeitpunkten \(t\) oder Ähnlichem zu indizieren?
  6. Lösen Sie das LP mit verschiedenen Solvern.
  7. Wieviel Kosten sparen Sie sich mit den zeitabhängigen Energiepreisen im Vergleich zum zugehörigen mittleren Energiepreis.
  8. Stellen Sie die Ergebnisse grafisch dar, beantworten Sie die Fragen, und interpretieren Sie die Ergebnisse.

Zeiten und Daten

Zeitpunkte, Zeitperioden und ihre Indizierung:

  • Samplingintervall \(\Delta t = 1\) h
  • Zeitpunkte \(t = 12, 13, \ldots, 20\) Uhr
  • Indizes der Zeitpunkte \(i = 0, 1, 2, \ldots, 8\)
  • Indizes der Zeitperioden \(j = 0, 1, 2, \ldots, 7\)

Daten:

  • Preise \(c_j\) in Cent/kWh für die Zeitperioden \(j = 0, 1, 2, \ldots, 7\)
Code 
import numpy as np
import matplotlib.pyplot as plt
import pyomo.environ as pyo
Code 
dt = 1  # h
times = np.arange(start=12, stop=20 + 1, step=dt)  # h, 12, 13, ..., 19, 20
time_indices = range(len(times))
period_indices = range(len(times) - 1)

prices  = np.array([10, 8, 12, 13, 11, 10, 13, 14])
prices_ = np.array([10, 8, 12, 13, 11, 10, 13, 14, 14])  # append last price for step-plotting

plt.figure(figsize=(5, 3))
plt.step(times, prices_, where='post', color='red', marker='.')
plt.xlabel('time (h)')
plt.ylabel('price (Cent/kWh)')
plt.grid()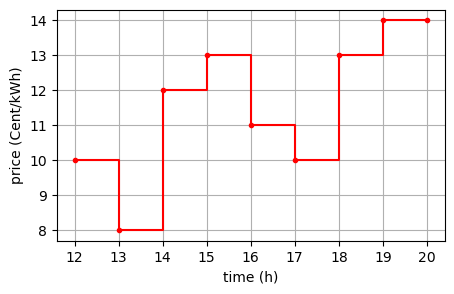

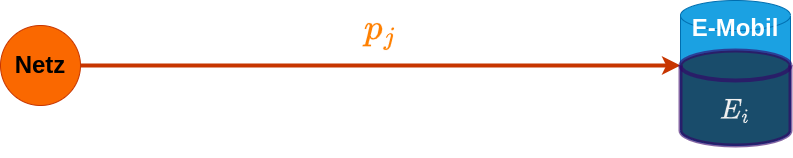
Energienetzwerk

Einfachstes Netzwerk

Modellierung

Entscheidungsvariablen:

  • \(p_j\) Ladeleistung in kW während der Zeitperioden mit Indizes \(j = 0, 1, 2, \ldots, 7\). Schranken: \(0 \leq p_j \leq 11\) kW.
  • \(E_i\) Energie der Batterie in kWh zu den Zeitpunkten mit Indizes \(i = 0, 1, 2, \ldots, 8\). Schranken: \(0 \leq E_i \leq 60\) kWh.

Zielfunktion: Minimiere die Ladekosten in Cent: \[\min \sum_{j=0}^7 c_j p_j \Delta t\]

Nebenbedingungen:

  • Die Energie der Batterie zu Beginn: \(E_0 = 0,40 \cdot 60 = 24\) kWh.
  • Die Energie der Batterie am Ende: \(E_8 = 60\) kWh.
  • Die Energie der Batterie am nächsten Zeitpunkt ergibt sich aus der Energie der Batterie zum aktuellen Zeitpunkt und der Ladeleistung in der dazwischenliegenden Zeitperiode mal der Periodendauer: \[E_{i+1} = E_i + p_i \Delta t \quad \forall i = 0, 1, 2, \ldots, 7\] Dabei wird angenommen, dass das Laden verlustfrei erfolgt.

Implementierung

Code 
model = pyo.ConcreteModel()

model.I = pyo.Set(initialize=time_indices)
model.J = pyo.Set(initialize=period_indices)

model.E = pyo.Var(model.I, bounds=(0.0, 60.0))
model.p = pyo.Var(model.J, bounds=(0.0, 11.0))

model.cost = pyo.Objective(expr=sum(prices[j]*model.p[j]*dt for j in model.J),
                          sense=pyo.minimize)

model.initial_energy = pyo.Constraint(expr = model.E[0] == 24.0)
model.final_energy = pyo.Constraint(expr = model.E[8] == 60.0)

@model.Constraint(model.I)  
def charging(model, i):
    if i < 8:
        return model.E[i + 1] == model.E[i] + model.p[i]*dt
    else:
        return pyo.Constraint.Skip

# model.pprint()
Code 
solver = pyo.SolverFactory('cbc')
# solver = pyo.SolverFactory('glpk')
# solver = pyo.SolverFactory('appsi_highs')
# solver = pyo.SolverFactory('gurobi')

results = solver.solve(model, tee=False)
print(f"status = {results.solver.status}")

print(f"minimal cost = {pyo.value(model.cost)/100.0:.2f} EUR")
status = ok
minimal cost = 3.41 EUR

Ergebnisse

Code 
E_sol_dict = model.E.extract_values()
E_sol = [E_sol_dict[i] for i in time_indices]

p_sol_dict = model.p.extract_values()
p_sol = [p_sol_dict[j] for j in period_indices]
p_sol_ = np.concatenate( (p_sol, [p_sol[-1]]) )

plt.figure(figsize=(5, 8))
plt.subplot(3, 1, 1)
plt.step(times, prices_, where='post', marker='.', color='red')
plt.xlabel('Zeit [h]')
plt.ylabel('Preis [Cent/kWh]')
plt.grid(True)

plt.subplot(3, 1, 2)
plt.step(times, p_sol_, where='post', marker='.', color='blue')
plt.xlabel('Zeit [h]')
plt.ylabel('Leistung [kW]')
plt.grid(True)

plt.subplot(3, 1, 3)
plt.plot(times, E_sol, marker='.', color='green')
plt.xlabel('Zeit [h]')
plt.ylabel('Energie [kWh]')
plt.grid(True)

plt.tight_layout()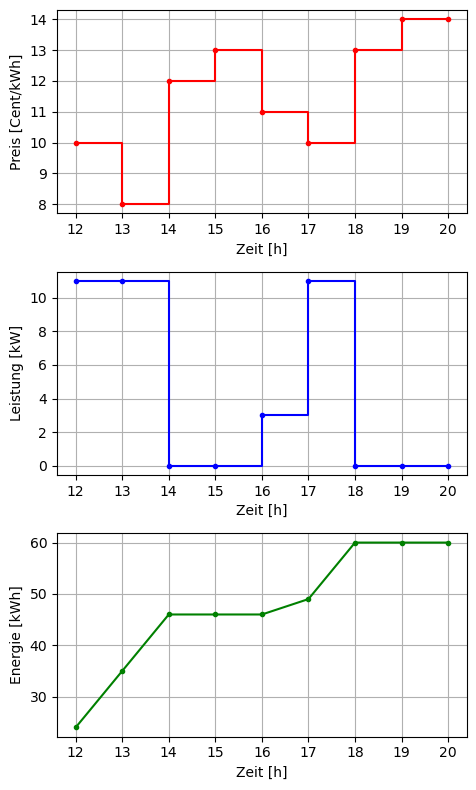

Das E-Mobil ist bereits um 18 Uhr vollgeladen.

Code 
price_mean = prices.mean()  # Cent/kWh
print(f"mean price = {price_mean:.2f} Cent/kWh")
mean price = 11.38 Cent/kWh
Code 
cost_mean_price = price_mean*(60 - 24)/100  # EUR
cost_prices = pyo.value(model.cost)/100.0   # EUR

print(f"cost with varying prices = {cost_prices:.2f} EUR")
print(f"cost with constant price = {cost_mean_price:.2f} EUR")

print(f"absolute saving = {cost_mean_price - cost_prices:.2f} EUR")
print(f"relative saving = {(cost_mean_price - cost_prices)/cost_mean_price*100:.2f} %")
cost with varying prices = 3.41 EUR
cost with constant price = 4.09 EUR
absolute saving = 0.68 EUR
relative saving = 16.73 %

Interpretation

Das Ladeproblem kann auch mit dem “Valley/Water Filling” Algorithmus gelöst werden. Dabei werden zuerst die Stunden mit den niedrigsten Preisen in maximalem Umfang zum Laden verwendet.

Übung: Laden inkl. fixen Lasten

Problemstellung

  1. Fügen Sie der Problemstellung folgende Features hinzu, und gehen Sie wieder in denselben Schritten (Modellieren des Energienetzwerks, Formulierung und Implementierung des LP) vor:
    • Ihr Haushalt hat zusätzlich zum Laden des E-Mobils einen Verbrauch (engl. demand), der durch folgenden Lastgang in kW gegeben ist: 3, 4, 2, 1, 5, 6, 5, 5.
    • Ihre PV-Anlage hat folgende stündliche Erzeugung in kW: 5, 5, 4, 3, 2, 1, 1, 0. Sie können überschüssige Energie in das Netz einspeisen.
  2. Vergleichen Sie in der um demand und PV erweiterten Problemstellung die minimalen Kosten bzgl. der zeitabhängigen Energiepreise mit den Kosten bzgl. des mittleren Energiepreises.