Transportproblem

Fabriken zu Lagerhäusern

Problemstellung

Das Unternehmen EiD (Erbsen in Dosen) produziert Dosenerbsen in seinen drei Fabriken F1, F2 und F3. Die produzierte Ware wird in die vier Lagerhäuser L1, L2, L3 und L4 transportiert. Die Produktionsmengen der Fabriken, die Bedarfsmengen der Lagerhäuser und die Kosten des Transports pro LKW-Ladung sind in der Parametertabelle Transportproblem_Beispiel.xlsx angeführt. Beachten Sie, dass die Summe der Produktionsmengen gleich der Summe der Bedarfsmengen ist.

Wir lösen das Transportproblem und stellen die Lösung dar.

Quelle: Hillier, Lieberman: Introduction to Operations Research. 10th edition, 2015. p. 319 ff.

Daten

Code

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import pyomo.environ as pyo

Code

# read data with pandas from excel file:
df = pd.read_excel("daten/Transportproblem_Beispiel.xlsx", index_col=0)
df

	L1	L2	L3	L4	Produktion
F1	464	513	654	867	75.0
F2	352	416	690	791	125.0
F3	995	682	388	685	100.0
Bedarf	80	65	70	85	NaN

Modellierung

Wir stellen die Daten des Transportproblems in einem ungerichteten Graphen dar, in dem die Fabriken und Lagerhäuser Knoten sind und jede Fabrik mit jedem Lagerhaus durch eine Kante verbunden ist. Die Kanten haben dabei die Transportkosten pro Mengeneinheit als Gewicht:

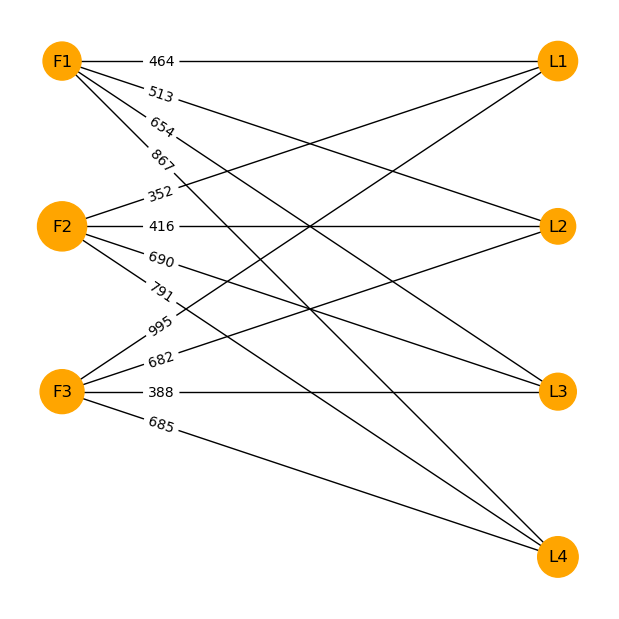
Für die Optimierung erhält jede Kante eine Flussvariable, die die transportierte Menge über die Kante angibt. Die Zielfunktion ist die Summe der Transportkosten pro Mengeneinheit multipliziert mit der zugehörigen transportierten Menge. Die Nebenbedingungen fixieren die Bedarfsmengen der Lagerhäuser und die Produktionsmengen der Fabriken.

Implementierung

Code

# make a list of the sources' names:
sources = df.index[:-1].tolist()
sources

['F1', 'F2', 'F3']

Code

# make a list of the targets' names:
targets = df.columns[:-1].tolist()
targets

['L1', 'L2', 'L3', 'L4']

Code

# make a dictionary of the targets' demands:
demand = df.loc['Bedarf', targets].to_dict()
demand

{'L1': 80.0, 'L2': 65.0, 'L3': 70.0, 'L4': 85.0}

Code

# make a dictionary of the sources' production quantities:
production = df.loc[sources, "Produktion"].to_dict()
production

{'F1': 75.0, 'F2': 125.0, 'F3': 100.0}

Code

# costs per unit as dataframe:
c = df.loc[sources, targets]
c

	L1	L2	L3	L4
F1	464	513	654	867
F2	352	416	690	791
F3	995	682	388	685

Code

model = pyo.ConcreteModel()

model.S = pyo.Set(initialize=sources)  # set of sources (plants)
model.T = pyo.Set(initialize=targets)  # set of targets (warehouses)

if True:  # use integrality constraint:
    print("using integrality constraint")
    model.x = pyo.Var(model.S, model.T, domain=pyo.NonNegativeIntegers)
else:     # relax the integrality constraint:
    print("relaxing integrality constraint")
    model.x = pyo.Var(model.S, model.T, domain=pyo.NonNegativeReals)

model.cost = pyo.Objective(expr=
    sum(model.x[s, t]*c.loc[s, t] for s in model.S for t in model.T), 
    sense=pyo.minimize)

@model.Constraint(model.S)
def demand_constraint(model, s):
    return sum(model.x[s, t] for t in model.T) == production[s]

@model.Constraint(model.T)
def production_constraint(model, t):
    return sum(model.x[s, t] for s in model.S) == demand[t]

# model.pprint()

using integrality constraint

Code

solver = pyo.SolverFactory('cbc')
# solver = pyo.SolverFactory('glpk')
# solver = pyo.SolverFactory('appsi_highs')
# solver = pyo.SolverFactory('gurobi')

results = solver.solve(model, tee=False)
print(f"status = {results.solver.status}")

print(f"minimal cost = {pyo.value(model.cost):.2f} EUR")

status = ok
minimal cost = 152535.00 EUR

Ergebnisse

Code

x_sol_dict = model.x.extract_values()
x_sol_dict

{('F1', 'L1'): 0.0,
 ('F1', 'L2'): 20.0,
 ('F1', 'L3'): 0.0,
 ('F1', 'L4'): 55.0,
 ('F2', 'L1'): 80.0,
 ('F2', 'L2'): 45.0,
 ('F2', 'L3'): 0.0,
 ('F2', 'L4'): 0.0,
 ('F3', 'L1'): 0.0,
 ('F3', 'L2'): 0.0,
 ('F3', 'L3'): 70.0,
 ('F3', 'L4'): 30.0}

Code

x_sol_df = pd.DataFrame(index=sources, columns=targets)
for item in x_sol_dict:
    x_sol_df.loc[item[0], item[1]] = x_sol_dict[item]
x_sol_df

	L1	L2	L3	L4
F1	0.0	20.0	0.0	55.0
F2	80.0	45.0	0.0	0.0
F3	0.0	0.0	70.0	30.0

Übung: Northern Airplane

Problemstellung

Die (erfundene) Northern Airplane Company baut Verkehrsflugzeuge. Ein wichtiger Schritt im Produktionsprozess ist die Herstellung und Installation des Düsentriebwerks. Die Produktion der Düsentriebwerke muss für die nächsten vier Monate geplant werden. Die vertraglich vereinbarten Liefermengen, die maximalen Produktionsmengen und die Produktions- und Lagerkosten pro Triebwerk in Mio. EUR sind für die kommenden 4 Monate in der folgenden Tabelle angeführt:

Monat	Liefermenge	max. Produktionsmenge	Produktionskosten pro Stück	Lagerkosten pro Stück
1	10	25	1.08	0.015
2	15	35	1.11	0.015
3	25	30	1.10	0.015
4	20	10	1.13	0.015

Aufgrund der Schwankungen der Produktionskosten kann es sich lohnen, einige der Triebwerke einen oder mehrere Monate vor ihrem geplanten Einbau zu fertigen. Der Nachteil dabei ist, dass die Lagerung dieser Triebwerke zusätzliche Kosten mit sich bringt.

Es soll der gesamtkostenoptimale Produktionszeitplan über die vier Monate bestimmt werden. Aufgaben:

Modellieren Sie in einer Exceldatei das Optimierungsproblem als Transportproblem:
- Verwenden Sie als Quellen die Produktionsmonate und als Ziele die Liefermonate.
- Überprüfen Sie, ob die Summe der Produktionsmengen gleich der Summe der Liefermengen ist, und fügen Sie bei Bedarf einen Dummy-Knoten ein.
- Verwenden Sie die “Big M Methode” (d. h. hier sehr große Stückkosten), um Verwendung von bestimmten Kanten zu vermeiden.
Implementieren Sie das Transportproblem.