Stromkosten minimieren

Problemstellung

Sie kaufen sich einen stationären Batteriespeicher für Ihr Haus und haben eine PV-Anlage auf dem Dach, die Sie mit dem Speicher verbinden. Sie möchten den Speicher so nutzen, dass Sie Ihre Stromkosten minimieren.

  1. Definieren Sie die Zeitpunkte, Zeitperioden und ihre Indizierung.
  2. Erstellen Sie einen Plot der PV-Erzeugung und des Stromverbrauchs über den Tag.
  3. Modellieren Sie das Energienetzwerk und fixieren Sie die Pfeilrichtung der Kanten.
  4. Basierend auf dieser Vorzeichenkonvention formulieren Sie das Optimierungsproblem:
    1. Definieren Sie die Entscheidungsvariablen inklusive Einheiten, Datentyp und Schranken.
    2. Formulieren Sie die Zielfunktion.
    3. Formulieren Sie die die Nebenbedingungen.
  5. Modellieren Sie das LP mit Pyomo. Warum ist es sinnvoll, die Entscheidungsvariablen mit Indizes \(0, 1, 2, \ldots\) anstatt mit Zeitpunkten \(t\) oder Ähnlichem zu indizieren?
  6. Lösen Sie das LP mit verschiedenen Solvern, und vergleichen Sie die Lösungen.
  7. Bestimmen Sie für jede Lösung den Autarkiegrad und den Eigenverbrauchsanteil, und vergleichen Sie diese zum Situation ohne Batteriespeicher.

Daten

Batteriespeicher:

  • Kapazität: 10 kWh
  • maximale Lade- und Entladeleistung: 5 kW
  • keine Selbstentladung. keine Lade- oder Entladeverluste
  • Anfangsladung: 5 kWh
  • Endladung: 5 kWh

Stromtarif:

  • Bezugspreis: 0.20 EUR/kWh
  • Einspeisevergütung: 0.12 EUR/kWh

Ertrag der PV-Anlage und Stromverbrauch des Haushalts in kW:

Code 
import numpy as np
import matplotlib.pyplot as plt
Code 
dt = 0.25  # h
times = np.arange(start=0, stop=24 + dt, step=dt)  # timestamps: 0, 0.25, 0.5, ..., 23.75, 24
periods = np.arange(start=0, stop=24, step=dt)     # start times of periods:  0, 0.25, 0.5, ..., 23.75
pv_power = np.zeros_like(periods)
pv_power[6*4:6*4 + 12*4] = 5*np.sin(2*np.pi/(6*4) * periods[:12*4] )  # PV power in kW

# source: https://www.bdew.de/energie/standardlastprofile-strom/
demand = np.array([87.7, 81.5, 76.2, 71.0, 65.8, 60.5, 55.6, 51.5, 48.5, 46.4, 44.9, 43.7, 42.7, 
                   41.8, 41.1, 40.6, 40.4, 40.4, 40.5, 40.6, 40.6, 40.6, 40.5, 40.6, 40.8, 41.6,
                   43.2, 46.1, 50.6, 56.7, 64.6, 74.2, 85.5, 97.9, 110.7, 123.4, 135.3, 145.9, 
                   155.1, 162.4, 167.8, 171.8, 175.5, 179.6, 184.9, 190.5, 195.7, 199.1, 200.4, 
                   198.8, 194.3, 186.7, 176.1, 163.9, 151.7, 141.3, 134.0, 129.1, 125.7, 122.7, 
                   119.3, 115.5, 111.7, 107.8, 104.2, 101.1, 99.1, 98.4, 99.5, 102.1, 106.2, 
                   111.7, 118.2, 125.5, 132.8, 139.8, 145.9, 150.7, 153.5, 153.9, 151.6, 147.4, 
                   142.8, 139.1, 136.9, 135.8, 134.8, 132.8, 129.0, 123.7, 117.0, 109.3, 101.0, 
                   92.3, 83.7, 75.7])
demand = demand/(np.sum(demand)*dt)*40  # demand load in kW, scaled to 40 kWh energy demand

plt.figure(figsize=(5, 3))
plt.plot(periods, pv_power, label='PV')
plt.plot(periods, demand, label='Verbrauch')
plt.xlabel('time (h)')
plt.ylabel('power (kW)')
plt.legend()
plt.grid()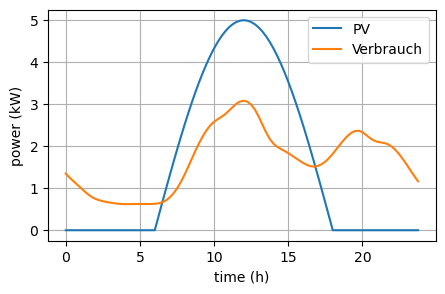

Überschlagsrechnung

Code 
# the demand energy is slightly greater than the produced PV energy:
print(f"demand energy: {np.sum(demand)*dt:.2f} kWh")
print(f"PV energy:     {np.sum(pv_power)*dt:.2f} kWh") 
demand energy: 40.00 kWh
PV energy:     38.18 kWh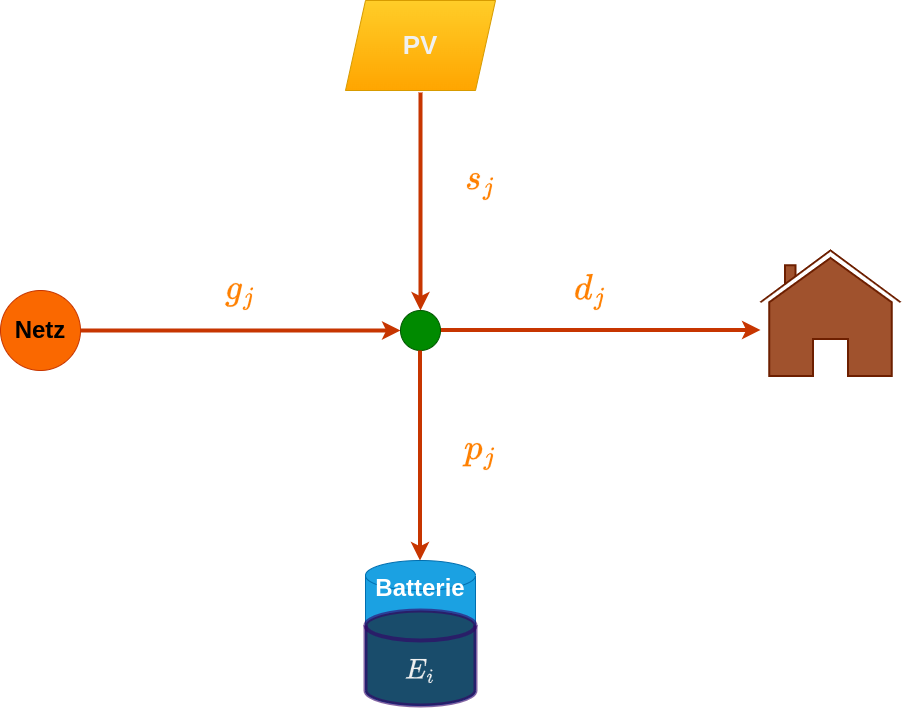
Code 
# rough estimate, more precisely a lower bound, for the cost: 
# (demand energy in kWh - PV energy in kWh) * 0.2 EUR/kWh
cost_rough = (np.sum(demand)*dt - np.sum(pv_power)*dt)*0.2
print(f"rough estimate of cost = {cost_rough:.2f} EUR")
rough estimate of cost = 0.36 EUR

Energienetzwerk

Energienetzwerk

Modellierung

Samping-Intervall: \(\Delta t\) = 0.25 Stunden

Entscheidungsvariablen:

  • \(p_j\) (Ent-)Ladeleistung in kW während der Zeitperioden mit Indizes \(j = 0, 1, 2, \ldots, 95\). Schranken: \(-5 \leq p_j \leq 5\) kW.
  • \(E_i\) Energie der Batterie in kWh zu den Zeitpunkten mit Indizes \(i = 0, 1, 2, \ldots, 96\). Schranken: \(0 \leq E_i \leq 10\) kWh.

Zielfunktion: Minimiere die aggregierten Netzkosten in EUR: \[\min \sum_{j=0}^{95} c(g_j \Delta t)\]

Nebenbedingungen:

  • Die Energie der Batterie zu Beginn: \(E_0 = 5\) kWh.
  • Die Energie der Batterie am Ende: \(E_{96} = 5\) kWh.
  • Die Energie der Batterie am nächsten Zeitpunkt ergibt sich aus der Energie der Batterie zum aktuellen Zeitpunkt und der Ladeleistung in der dazwischenliegenden Zeitperiode: \[E_{i+1} = E_i + p_i \Delta t \quad \forall i = 0, 1, 2, \ldots, 95\]
  • Netzwerkgleichungen: \[g_j + s_j = d_j + p_j \quad \forall j = 0, 1, 2, \ldots, 95.\]

Modellierungstrick: Die Zielfunktion \(\sum_{j=0}^{95} c(g_j \Delta t)\) ist nicht-linear, genauer: die Funktion \(c\) ist konvex und stückweise linear: \[ c(g_j \Delta t) = \begin{cases} 0.2 g_j \Delta t & \text{falls } g_j \geq 0 \\ 0.12 g_j \Delta t & \text{falls } g_j < 0 \end{cases} \]

In der folgenden Abbildung betrachten wir der Einfachheit halber nur eine Zeitperiode:

Code 
g_pos = np.linspace(  0, 10)
g_neg = np.linspace(-10,  0)
g_all = np.linspace(-10, 10)

c_pos = 0.20  # Preis für Netzbezug in EUR/kWh
c_neg = 0.12  # Preis für Einspeisevergütung in EUR/kWh

plt.figure(figsize=(5, 3))
plt.plot(g_pos*dt, c_pos*g_pos*dt, 'r', label="Netzbezug")
plt.plot(g_neg*dt, c_neg*g_neg*dt, 'g', label="Netzeinspeisung")
plt.plot(g_all*dt, c_pos*g_all*dt, '--r', alpha=0.5)
plt.plot(g_all*dt, c_neg*g_all*dt, '--g', alpha=0.5)
plt.xlabel("Energie (kWh)")
plt.ylabel("Kosten (EUR)")
plt.legend()
plt.grid()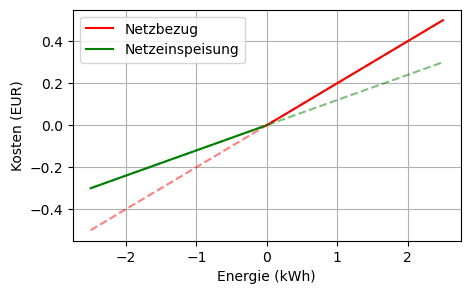

Die Minimierung einer solchen Zielfunktion lässt sich in einem LP mit zusätzlichen Variablen \(k_j\) und zusätzlichen Nebenbedingungen umsetzen: \[ \begin{aligned} \text{min.} \; & \sum_{j=0}^{95} k_j \\ \text{s. t.}\; & 0.2 g_j \Delta t \leq k_j \quad \forall j = 0, 1, 2, \ldots, 95\\ & 0.12 g_j \Delta t \leq k_j \quad \forall j = 0, 1, 2, \ldots, 95\\ \end{aligned} \]

Implementierung

Code 
import pyomo.environ as pyo
Code 
n = len(periods)                 # 96
time_indices = np.arange(n + 1)  # 0, 1, ..., 95, 96
period_indices = range(n)        # 0, 1, ..., 95
Code 
model = pyo.ConcreteModel()

model.I = pyo.Set(initialize=time_indices)
model.J = pyo.Set(initialize=period_indices)

model.E = pyo.Var(model.I, bounds=(0.0, 10.0))
model.p = pyo.Var(model.J, bounds=(-5.0, 5.0))
model.g = pyo.Var(model.J, domain = pyo.Reals)
model.k = pyo.Var(model.J, domain = pyo.Reals)

model.cost = pyo.Objective(expr=sum(model.k[j] for j in model.J),
                          sense=pyo.minimize)

model.initial_energy = pyo.Constraint(expr = model.E[0] == 5.0)
model.final_energy = pyo.Constraint(expr = model.E[n] == 5.0)

@model.Constraint(model.J)
def cost_buy(model, j):
    return 0.2*model.g[j]*dt <= model.k[j]

@model.Constraint(model.J)
def cost_sell(model, j):
    return 0.12*model.g[j]*dt <= model.k[j]

@model.Constraint(model.J)
def node(model, j):
    return model.g[j] == model.p[j] +  demand[j] - pv_power[j]

@model.Constraint(model.I)
def charging(model, i):
    if i < n:
        return model.E[i + 1] == model.E[i] + model.p[i] * dt
    else:
        return pyo.Constraint.Skip

# model.pprint()
Code 
solver = pyo.SolverFactory('cbc')
solver = pyo.SolverFactory('glpk')
# solver = pyo.SolverFactory('appsi_highs')
# solver = pyo.SolverFactory('gurobi')

results = solver.solve(model, tee=False)
print(f"status = {results.solver.status}")

print(f"minimal cost = {pyo.value(model.cost):.2f} EUR")
status = ok
minimal cost = 0.83 EUR

Ergebnisse

Hinweis: Vergleichen Sie die Lösungen von verschiedenen Solvern!

Code 
E_sol_dict = model.E.extract_values()
E_sol = [E_sol_dict[i] for i in time_indices]

p_sol_dict = model.p.extract_values()
p_sol = [p_sol_dict[j] for j in period_indices]

plt.figure(figsize=(5, 8))
plt.subplot(3, 1, 1)
plt.plot(periods, pv_power, label='PV')
plt.plot(periods, demand, label='Verbrauch')
plt.xlabel('Zeit [h]')
plt.ylabel('Leistung [kW]')
plt.legend()
plt.grid(True)

plt.subplot(3, 1, 2)
plt.plot(periods, p_sol, marker='.', color='blue')
plt.xlabel('Zeit [h]')
plt.ylabel('Batterieleistung [kW]')
plt.grid(True)

plt.subplot(3, 1, 3)
plt.plot(times, E_sol, marker='.', color='green')
plt.xlabel('Stunde')
plt.ylabel('Energiestand [kWh]')
plt.grid(True)

plt.tight_layout()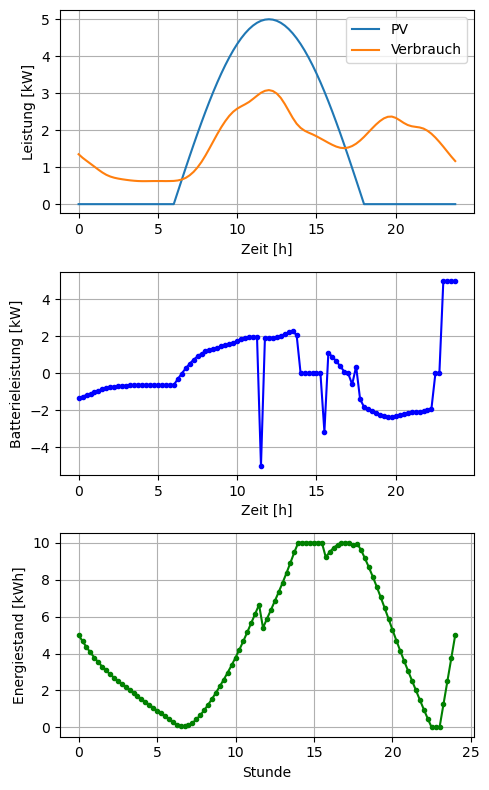

Code 
g_sol_dict = model.g.extract_values()
g_sol = [g_sol_dict[j] for j in period_indices]

plt.figure(figsize=(5, 3))
plt.plot(periods, pv_power - demand, label='PV minus Verbrauch')
plt.plot(periods, g_sol, label='Netz')
plt.xlabel('Zeit [h]')
plt.ylabel('Leistung [kW]')
plt.legend()
plt.grid(True)
plt.tight_layout()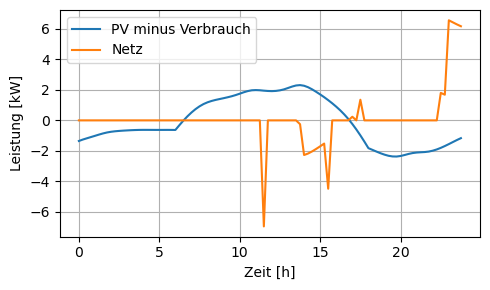

Code 
# Autarkiegrad und Eigenverbrauchsanteil:

feed_in = -np.minimum(g_sol, 0) # Einspeiseleistung in kW
Eigenverbrauch = np.sum(pv_power*dt) - np.sum(feed_in*dt)
print(f"Eigenverbrauch = {Eigenverbrauch:.1f} kWh")

PV_Ertrag = np.sum(pv_power*dt)
Eigenverbrauchsanteil = Eigenverbrauch/PV_Ertrag
print(f"Eigenverbrauchsanteil = {Eigenverbrauchsanteil*100:.1f} %")

Gesamtverbrauch = np.sum(demand*dt)
Autarkiegrad = Eigenverbrauch/Gesamtverbrauch
print(f"Autarkiegrad = {Autarkiegrad*100:.1f} %")
Eigenverbrauch = 32.4 kWh
Eigenverbrauchsanteil = 84.8 %
Autarkiegrad = 80.9 %
Code 
# Zum Vergleich: Autarkiegrad und Eigenverbrauchsanteil ohne Speicher:

Eigenverbrauch = np.sum(np.minimum(pv_power, demand)*dt)
print(f"Eigenverbrauch = {Eigenverbrauch:.1f} kWh")

Eigenverbrauchsanteil = Eigenverbrauch/PV_Ertrag
print(f"Eigenverbrauchsanteil = {Eigenverbrauchsanteil*100:.1f} %")

Autarkiegrad = Eigenverbrauch/Gesamtverbrauch
print(f"Autarkiegrad = {Autarkiegrad*100:.1f} %")
Eigenverbrauch = 22.4 kWh
Eigenverbrauchsanteil = 58.7 %
Autarkiegrad = 56.1 %

Interpretation:

  • Die verschiedenen Solver liefern wie zu erwarten dieselben minimalen Kosten. Die Lösungen unterscheiden sich jedoch in den Werten der Entscheidungsvariablen. Dies liegt daran, dass die Solver unterschiedliche Algorithmen verwenden, um die Lösung zu finden.
  • Eingenverbrauch, Eingenverbrauchsanteil und Autarkiegrad sind bei allen Lösungen gleich.

Übung: Eigenverbrauch maximieren

Problemstellung

  1. Begründen Sie mathematisch, warum das Maximieren des Eigenverbrauchs äquivalent zum Maximieren des Eigenverbrauchsanteils und des Autarkiegrads ist.
  2. Modellieren Sie ein Optimierungsproblem, das den Eigenverbrauch maximiert.
  3. Vergleichen Sie Ihre Lösung mit der Lösung des Problems, das die Netzkosten minimiert. Konnten Sie den Eigenverbrauch erhöhen?

Hinweis: Lesen Sie bei Bedarf den Abschnitt Eigenverbrauchsanteil und Autarkiegrad.