Kürzester Weg

LP-Formulierung

Problemstellung

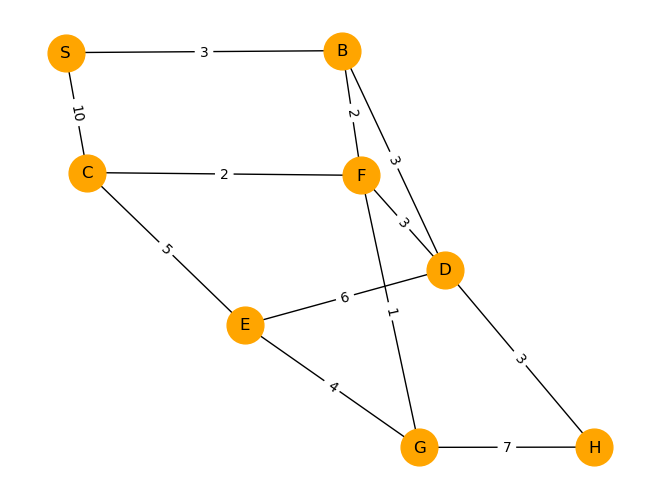
Durch die Daten unten ist der ungerichtete Graph der Abbildung Abbildung 1 gegeben, dessen Kantengewichte die Strecken zwischen den Endknoten der Kanten angegeben hat. Wir bestimmen mittels der LP-Formulierung die kürzesten Wege vom Konten \(S\) zu allen anderen Knoten.

Daten

Code

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import pyomo.environ as pyo

Code

weight = {
    ('S', 'B'): 3,
    ('S', 'C'): 10,
    ('B', 'D'): 3,
    ('D', 'E'): 6,
    ('D', 'F'): 3,
    ('E', 'C'): 5,
    ('B', 'F'): 2,
    ('C', 'F'): 2,
    ('E', 'G'): 4,
    ('G', 'H'): 7,
    ('F', 'G'): 1,
    ('D', 'H'): 3}

Modellierung

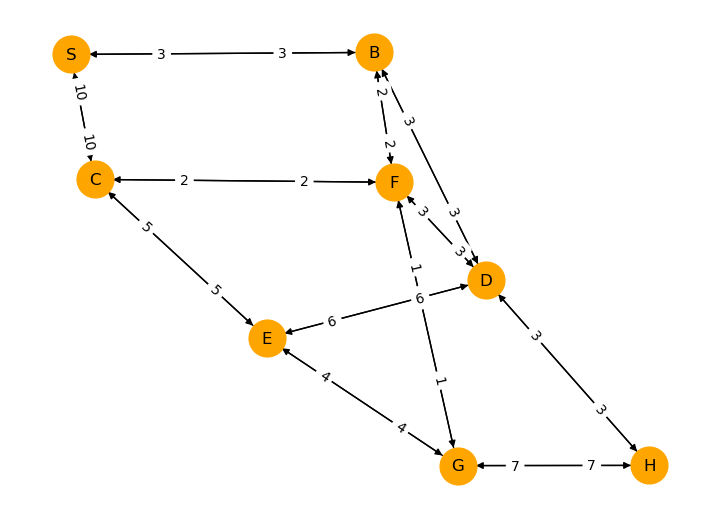
Wie im Abschnitt Kürzester Weg beschrieben formulieren wir den ungerichteten Graphen um zu einem äquivalenten gerichteten Graphen mit den Kantengewichten \(w_{ij}\) auf den Kanten zwischen den Knoten \(i\) und \(j\). Die Abbildung Abbildung 2 zeigt den zugehörigen gerichteten Graphen.

Implementierung

Code

nodes = ['S', 'B', 'C', 'D', 'E', 'F', 'G', 'H']
weight_reverse = {(j, i): v for (i, j), v in weight.items()}
weight_directed = weight | weight_reverse # union of the two dictionaries
edges =  list(weight_directed.keys())

ext_flow = {node: -1 for node in nodes}
ext_flow['S'] = len(nodes) - 1

Code

model = pyo.ConcreteModel()

model.N = pyo.Set(initialize=nodes)      # set of nodes
model.E = pyo.Set(initialize=edges)      # set of edges

model.x = pyo.Var(model.E, domain=pyo.NonNegativeReals)

model.obj = pyo.Objective(expr=
    sum(weight_directed[i, j]*model.x[i, j] for (i, j) in edges),
    sense=pyo.minimize)

@model.Constraint(model.N)
def node_balance(model, i):
    return sum(model.x[i, n] for n in model.N if (i, n) in model.E) - \
           sum(model.x[n, i] for n in model.N if (n, i) in model.E) == \
           ext_flow[i]

Code

solver = pyo.SolverFactory('cbc')
# solver = pyo.SolverFactory('glpk')
# solver = pyo.SolverFactory('appsi_highs')
# solver = pyo.SolverFactory('gurobi')

results = solver.solve(model, tee=False)
print(f"status = {results.solver.status}")

print(f"minimum objective value = {pyo.value(model.obj):.2f}")

status = ok
minimum objective value = 46.00

Ergebnisse

Code

x_sol_dict = model.x.extract_values()
# x_sol_dict

# formatted print out of solution:
for edge in edges:
    if x_sol_dict[edge] > 0:
        print(f"flow on edge {edge} = {x_sol_dict[edge]:.2f}")

flow on edge ('S', 'B') = 7.00
flow on edge ('B', 'D') = 2.00
flow on edge ('B', 'F') = 4.00
flow on edge ('F', 'G') = 2.00
flow on edge ('D', 'H') = 1.00
flow on edge ('F', 'C') = 1.00
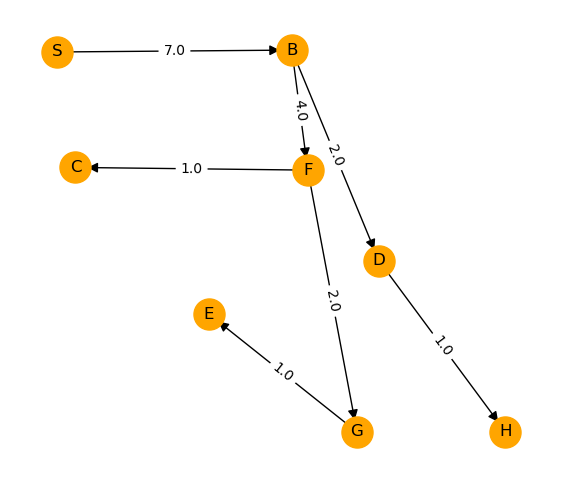
flow on edge ('G', 'E') = 1.00

In Abbildung Abbildung 3 ist die Lösung des Problems dargestellt.