Erbsen in Dosen

Problemstellung

Wir betrachten wieder das Unternehmen EiD (Erbsen in Dosen), das Dosenerbsen in drei Fabriken F1, F2 und F3 produziert. Die produzierte Ware wird zu vier Lagerhäusern L1, L2, L3 und L4 transportiert. Das Unternehmen kann Kosten einsparen, indem es seinen eigenen Fuhrpark aufgibt und stattdessen Spediteure für den Transport der Erbsenkonserven einsetzt. Da kein einziges Speditionsunternehmen das gesamte Gebiet mit allen Konservenfabriken und Lagerhäusern bedient, müssen viele der Sendungen mindestens einmal auf einen anderen LKW umgeladen werden. Die möglichen Routen von einer Fabrik zu einem Lagerhaus können über andere Fabriken, vier Umschlagspunkte und andere Fabriken gehen.

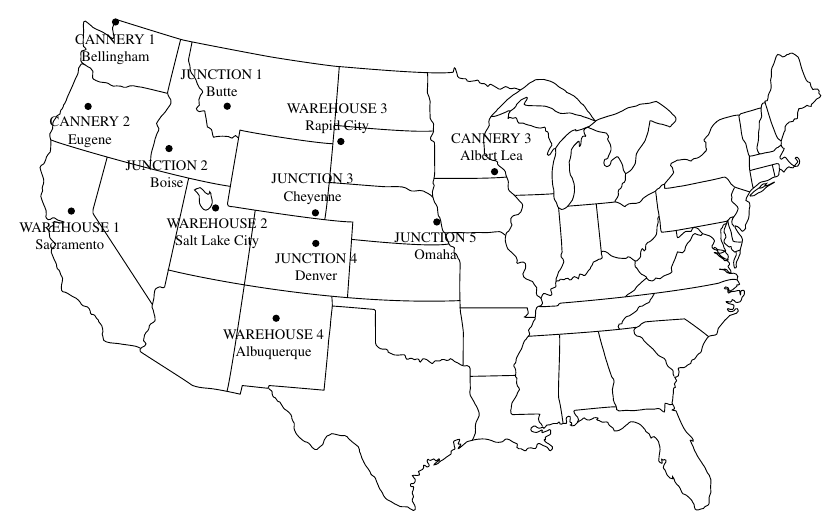
Beispiel eines Umladeproblems. Quelle: Hillier, Lieberman: Introduction to Operations Research. 10th edition, 2015. Web Chapter 23-1, p. 23-4

Die Produktionsmengen der Fabriken, die Bedarfsmengen der Lagerhäuser und die Kosten des Transports pro LKW-Ladung sind in der Parametertabelle Umladeproblem_Beispiel.xlsx angeführt.

Gesucht sind die Routen und deren Warenmengen, sodass die Gesamtkosten minimal sind. Wir lösen dieses Umladeproblem und stellen die Lösung dar.

Quelle: Hillier, Lieberman: Introduction to Operations Research. 10th edition, 2015. Web Chapter 23-1, p. 23-3 ff.

Daten

Code 
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import pyomo.environ as pyo
Code 
# read cost table data from file:
df = pd.read_excel("daten/Umladeproblem_Beispiel.xlsx", index_col=0)
df
S1 S2 S3 J1 J2 J3 J4 J5 T1 T2 T3 T4 production
from\to
S1 NaN 146.0 NaN 324.0 286.0 NaN NaN NaN 452.0 505.0 NaN 871.0 75.0
S2 146.0 NaN NaN 373.0 212.0 570.0 609.0 NaN 335.0 407.0 688.0 784.0 125.0
S3 NaN NaN NaN 658.0 NaN 405.0 419.0 158.0 NaN 685.0 359.0 673.0 100.0
J1 322.0 371.0 656.0 NaN 262.0 398.0 430.0 NaN 503.0 234.0 329.0 NaN NaN
J2 284.0 210.0 NaN 262.0 NaN 406.0 421.0 644.0 305.0 207.0 464.0 558.0 NaN
J3 NaN 569.0 403.0 398.0 406.0 NaN 81.0 272.0 597.0 253.0 171.0 282.0 NaN
J4 NaN 608.0 418.0 431.0 422.0 81.0 NaN 287.0 613.0 280.0 236.0 229.0 NaN
J5 NaN NaN 158.0 NaN 647.0 274.0 288.0 NaN 831.0 501.0 293.0 482.0 NaN
T1 453.0 336.0 NaN 505.0 307.0 599.0 615.0 831.0 NaN 359.0 706.0 587.0 NaN
T2 505.0 407.0 683.0 235.0 208.0 254.0 281.0 500.0 357.0 NaN 362.0 341.0 NaN
T3 NaN 687.0 357.0 329.0 464.0 171.0 236.0 290.0 705.0 362.0 NaN 457.0 NaN
T4 868.0 781.0 670.0 NaN 558.0 282.0 229.0 480.0 587.0 340.0 457.0 NaN NaN
demand NaN NaN NaN NaN NaN NaN NaN NaN 80.0 65.0 70.0 85.0 NaN

Modellierung

Wir stellen die Daten des Umladeproblems in einem gerichteten Graphen dar, in dem die Fabriken (Quellen, sources), Umschlagspunkte (junctions) und Lagerhäuser (Ziele, targets) Knoten sind und die gerichteten Kanten die möglichen Transportwege angeben. Die Kanten haben dabei die Transportkosten pro Mengeneinheit als Gewicht:

Graph des Umladeproblems

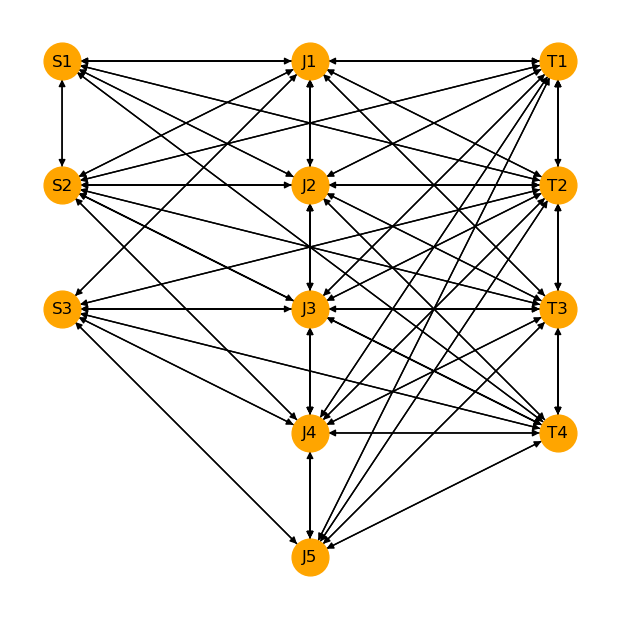
Für die Optimierung erhält jede Kante eine Flussvariable, die die transportierte Menge über die Kante angibt. Die Zielfunktion ist die Summe der Transportkosten pro Mengeneinheit multipliziert mit der zugehörigen transportierten Menge. Die Nebenbedingungen fixieren die Bedarfsmengen der Lagerhäuser, die Produktionsmengen der Fabriken und die Mengenbilanzen der Umschlagspunkte.

Implementierung

Code 
sources = df.index[:3].tolist()
junctions = df.index[3:8].tolist()
targets = df.index[8:12].tolist()
nodes = sources + junctions + targets

demand = df.loc['demand', targets].to_dict()
production = df.loc[sources, "production"].to_dict()

# costs per unit as pandas data frame:
c = df.loc[nodes, nodes]  # includes NaN entries
# print(c)

# edges as list of tuples:
edges = [(n, m) for n in nodes for m in nodes if not np.isnan(c.loc[n, m])]
# print(edges)
Code 
model = pyo.ConcreteModel()

model.S = pyo.Set(initialize=sources)    # set of sources
model.J = pyo.Set(initialize=junctions)  # set of junctions
model.T = pyo.Set(initialize=targets)    # set of targets
model.N = pyo.Set(initialize=nodes)      # set of nodes
model.E = pyo.Set(initialize=edges)      # set of edges

if True:  # use integrality constraint:
    print("using integrality constraint")
    model.x = pyo.Var(model.E, domain=pyo.NonNegativeIntegers)
else:     # relax the integrality constraint:
    print("relaxing integrality constraint")
    model.x = pyo.Var(model.E, domain=pyo.NonNegativeReals)

model.cost = pyo.Objective(expr=
    sum(model.x[n, m]*c.loc[n, m] for (n, m) in model.E),
    sense=pyo.minimize)

@model.Constraint(model.S)
def production_constraint(model, s):
    return sum(model.x[s, n] for n in model.N if (s, n) in model.E) - \
           sum(model.x[n, s] for n in model.N if (n, s) in model.E) == \
           production[s]

@model.Constraint(model.T)
def demand_constraint(model, t):
    return sum(model.x[n, t] for n in model.N if (n, t) in model.E) - \
           sum(model.x[t, n] for n in model.N if (t, n) in model.E) == \
           demand[t]

@model.Constraint(model.J)
def junction_constraint(model, j):
    return sum(model.x[j, n] for n in model.N if (j, n) in model.E) - \
           sum(model.x[n, j] for n in model.N if (n, j) in model.E) == 0

# model.pprint()
using integrality constraint
Code 
solver = pyo.SolverFactory('cbc')
# solver = pyo.SolverFactory('glpk')
# solver = pyo.SolverFactory('appsi_highs')
# solver = pyo.SolverFactory('gurobi')

results = solver.solve(model, tee=False)
print(f"status = {results.solver.status}")

print(f"minimal cost = {pyo.value(model.cost):.2f} EUR")
status = ok
minimal cost = 145175.00 EUR

Ergebnisse

Code 
x_sol_dict = model.x.extract_values()
# x_sol_dict

# formatted print out of solution:
for edge in edges:
    if x_sol_dict[edge] > 0:
        print(f"flow on edge {edge} = {x_sol_dict[edge]}.")
flow on edge ('S1', 'J2') = 75.0.
flow on edge ('S2', 'T1') = 80.0.
flow on edge ('S2', 'T2') = 45.0.
flow on edge ('S3', 'J5') = 30.0.
flow on edge ('S3', 'T3') = 70.0.
flow on edge ('J2', 'T2') = 75.0.
flow on edge ('J5', 'T4') = 30.0.
flow on edge ('T2', 'T4') = 55.0.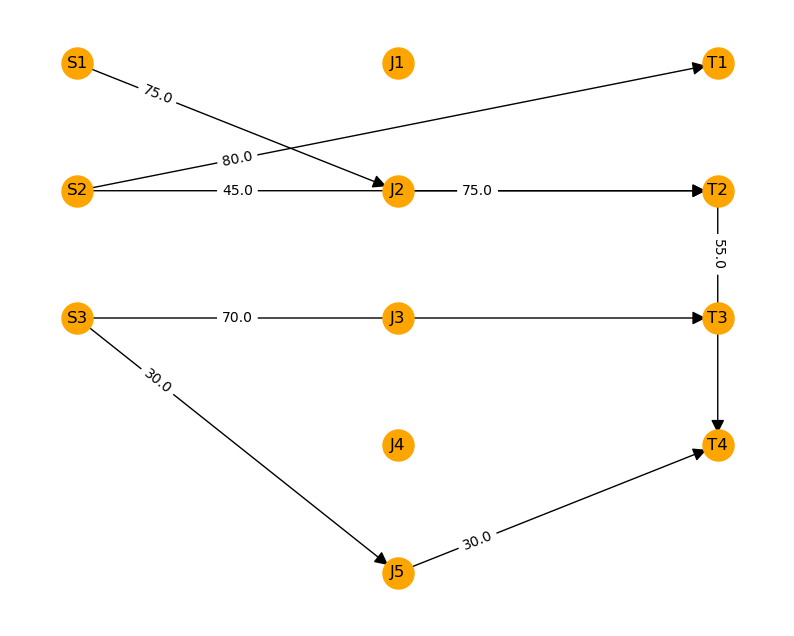

Optimale Lösung des Umladeproblems
Code 
x_sol_df = pd.DataFrame(index=nodes, columns=nodes)
for item in x_sol_dict:
    x_sol_df.loc[item[0], item[1]] = x_sol_dict[item]
x_sol_df
S1 S2 S3 J1 J2 J3 J4 J5 T1 T2 T3 T4
S1 NaN 0.0 NaN 0.0 75.0 NaN NaN NaN 0.0 0.0 NaN 0.0
S2 0.0 NaN NaN 0.0 0.0 0.0 0.0 NaN 80.0 45.0 0.0 0.0
S3 NaN NaN NaN 0.0 NaN 0.0 0.0 30.0 NaN 0.0 70.0 0.0
J1 0.0 0.0 0.0 NaN 0.0 0.0 0.0 NaN 0.0 0.0 0.0 NaN
J2 0.0 0.0 NaN 0.0 NaN 0.0 0.0 0.0 0.0 75.0 0.0 0.0
J3 NaN 0.0 0.0 0.0 0.0 NaN 0.0 0.0 0.0 0.0 0.0 0.0
J4 NaN 0.0 0.0 0.0 0.0 0.0 NaN 0.0 0.0 0.0 0.0 0.0
J5 NaN NaN 0.0 NaN 0.0 0.0 0.0 NaN 0.0 0.0 0.0 30.0
T1 0.0 0.0 NaN 0.0 0.0 0.0 0.0 0.0 NaN 0.0 0.0 0.0
T2 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 NaN 0.0 55.0
T3 NaN 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 NaN 0.0
T4 0.0 0.0 0.0 NaN 0.0 0.0 0.0 0.0 0.0 0.0 0.0 NaN
Code 
# compare with the problem data:
df
S1 S2 S3 J1 J2 J3 J4 J5 T1 T2 T3 T4 production
from\to
S1 NaN 146.0 NaN 324.0 286.0 NaN NaN NaN 452.0 505.0 NaN 871.0 75.0
S2 146.0 NaN NaN 373.0 212.0 570.0 609.0 NaN 335.0 407.0 688.0 784.0 125.0
S3 NaN NaN NaN 658.0 NaN 405.0 419.0 158.0 NaN 685.0 359.0 673.0 100.0
J1 322.0 371.0 656.0 NaN 262.0 398.0 430.0 NaN 503.0 234.0 329.0 NaN NaN
J2 284.0 210.0 NaN 262.0 NaN 406.0 421.0 644.0 305.0 207.0 464.0 558.0 NaN
J3 NaN 569.0 403.0 398.0 406.0 NaN 81.0 272.0 597.0 253.0 171.0 282.0 NaN
J4 NaN 608.0 418.0 431.0 422.0 81.0 NaN 287.0 613.0 280.0 236.0 229.0 NaN
J5 NaN NaN 158.0 NaN 647.0 274.0 288.0 NaN 831.0 501.0 293.0 482.0 NaN
T1 453.0 336.0 NaN 505.0 307.0 599.0 615.0 831.0 NaN 359.0 706.0 587.0 NaN
T2 505.0 407.0 683.0 235.0 208.0 254.0 281.0 500.0 357.0 NaN 362.0 341.0 NaN
T3 NaN 687.0 357.0 329.0 464.0 171.0 236.0 290.0 705.0 362.0 NaN 457.0 NaN
T4 868.0 781.0 670.0 NaN 558.0 282.0 229.0 480.0 587.0 340.0 457.0 NaN NaN
demand NaN NaN NaN NaN NaN NaN NaN NaN 80.0 65.0 70.0 85.0 NaN