Stationäre Probleme
Unter stationären Problemen verstehen wir Optimierungsprobleme, die sich auf einen bestimmten Zeitpunkt beziehen oder keine zeitliche Entwicklung der Entscheidungsvariablen beinhalten und eine “Dauerlösung” suchen.
Transportproblem
Problemstellung
Bei einem Transportproblem (Englisch: transportation problem) geht es darum, eine Ware von gewissen Lieferzentren, auch Quellen genannt, an gewisse Empfangszentren, auch Ziele genannt, so zu verteilen, dass die Gesamtverteilungskosten minimiert werden. Es muss dabei nicht unbedingt um Waren, Liefer- und Empfangszentren gehen. Wichtig ist die Struktur von Quellen und Zielen.
Gegeben sind dabei im Detail:
- die Quellen (Lieferzentren, sources) und ihre Produktionsmengen
- die Ziele (Empfangszentren, targets) und ihre Bedarfsmengen
- die Transportkosten pro Mengeneinheit der Ware von jeder Quelle zu jedem Ziel
Gesucht sind die Warenmengen, die von jeder Quelle zu jedem Ziel transportiert werden sollen, sodass die Gesamtkosten minimal sind.
Das Transportproblem kann als ungerichteter Graph dargestellt werden, in dem die Quellen und Ziele als Knoten modelliert sind und jede Quelle mit jedem Ziel durch eine Kante verbunden ist. Die Kanten haben dabei die Transportkosten pro Mengeneinheit als Gewicht, siehe das Beispiel: Transportproblem.
LP-Formulierung
Entscheidungsvariablen: Anzahlen \(x_{ij}\) der zu verteilenden Warenmengen von Quelle \(i\) an Ziel \(j\), \(i = 1, 2, \ldots, m\), \(j = 1, 2, \ldots, n\).
Zielfunktion: \(\sum_{i=1}^m \sum_{j=1}^n c_{ij} x_{ij}\) mit Transportkosten \(c_{ij}\) pro Wareneinheit von jeder Quelle \(i\) zu jedem Ziel \(j\)
Nebenbedingungen:
- \(\sum_{j=1}^n x_{ij} = s_i\) für alle \(i = 1, 2, \ldots, m\), mit \(s_i\) der Produktionsmenge der Quelle \(i\)
- \(\sum_{i=1}^m x_{ij} = d_j\) für alle \(j = 1, 2, \ldots, n\), mit \(d_j\) der Bedarfsmenge des Ziels \(j\)
- \(x_{ij} \geq 0\) für alle \(i\) und \(j\)
Dabei wird implizit angenommen, dass die Transportkosten linear in den Warenmengen \(x_{ij}\) sind.
Bedingung für die Existenz zulässiger Punkte: Ein Transportproblem hat genau dann zulässige Punkte, wenn gilt, dass die Summe der Produktionsmengen gleich der Summe der Bedarfsmengen ist: \(\sum_{i=1}^m s_i = \sum_{j=1}^n d_j.\)
Ganzzahlige Lösungen: Wenn alle \(s_i\) und \(d_j\) Werte ganzzahlig sind, dann sind die Ecken des Nebenbedingungspolyeders auch ganzzahlig. Unter diesen Umständen ist der vom Simplex-Algorithmus berechnete optimale Punkt daher ganzzahlig, und es müssen keine zusätzlichen Ganzzahligkeitsnebenbedingungen verwendet werden.
Algorithmik: Transportprobleme sind eine besondere Art von LPs und können daher mit dem Simplex-Algorithmus gelöst werden. Die besondere Struktur von Transportprobleme kann jedoch ausgenutzt werden, um den Simplex-Algorithmus effizienter zu machen. Siehe z. B. Hillier, Lieberman: Introduction to Operations Research. 10th edition, 2015. p. 333 ff. für den die “transportation simplex method” und Wikipedia: Netzwerk-Simplexmethode.
Modellierungstricks
Dummy-Ziel: Wenn die Summe der Produktionsmengen größer ist als die Summe der Bedarfsmengen, kann man ein Dummy-Ziel einführen, das den restlichen Bedarf mit Null Transportkosten übernimmt, siehe Abbildungen Abbildung 1 und Abbildung 2.
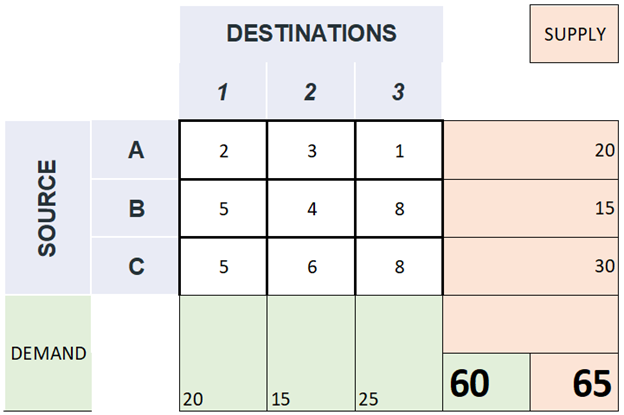
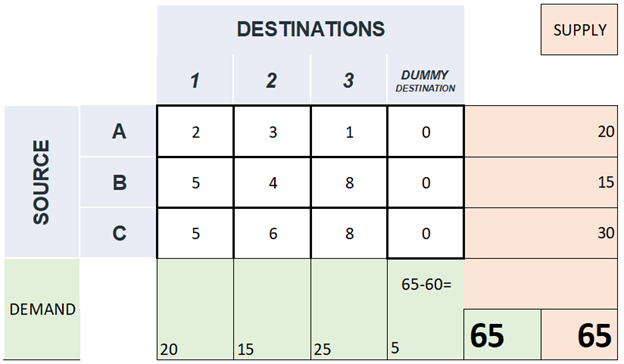
Quelle: Link
Dummy-Quelle: Wenn die Summe der Bedarfsmengen größer ist als die Summe der Produktionsmengen, kann man eine Dummy-Quelle einführen, die die restliche Produktion mit Null Transportkosten übernimmt, siehe Abbildungen Abbildung 3 und Abbildung 4.
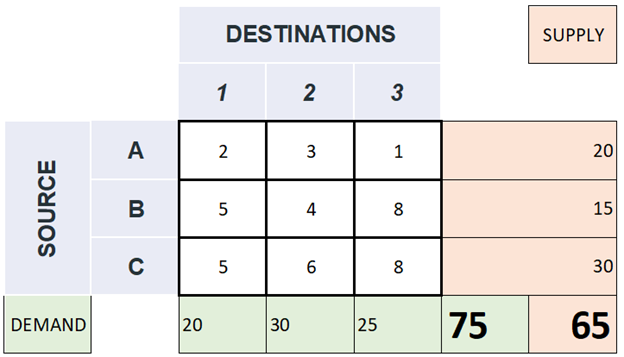
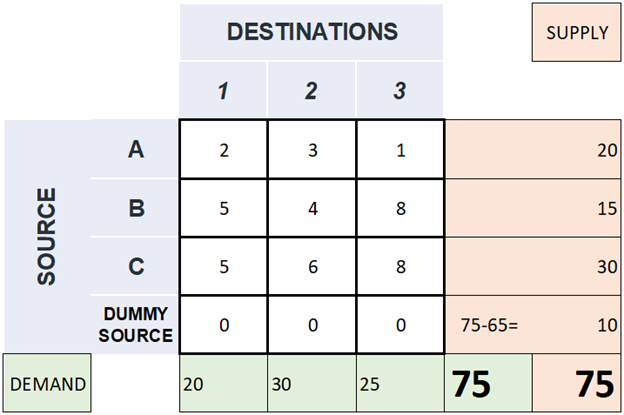
Quelle: Link
Zuordnungsproblem
Problemstellung
- Es gibt \(n\) Tätigkeiten (Aufträge, englisch: tasks, jobs) und \(n\) Arbeiter (Auftragsempfänger, englisch: assignees).
- Jedem Arbeiter wird genau eine Tätigkeit zugeordnet.
- Wenn dem Arbeiter \(i\) die Tätigkeit \(j\) zugeordnet wird, entstehen Kosten \(c_{ij}\).
- Ziel ist es, eine gesamtkostenoptimale Zuordnung zu bestimmen.
Es muss dabei nicht unbedingt um Tätigkeiten und Arbeiter gehen. Wichtig ist die Struktur von Quellen und Zielen. Das Zuordnungsproblem ist ein Spezialfall des Transportproblems und kann ebenso als ungerichteter Graph dargestellt werden.
LP-Formulierung
Binäre Entscheidungsvariablen: \(x_{ij}\) für \(i, j = 1, 2, \ldots, n\) mit \(x_{ij} = 1\), wenn dem Arbeiter \(i\) die Tätigkeit \(j\) zugeordnet wird, andernfalls \(0\).
Zielfunktion: \(\sum_{i=1}^n \sum_{j=1}^n c_{ij} x_{ij}\)
Nebenbedingungen
- \(\sum_{j=1}^n x_{ij} = 1\) für alle \(i = 1, 2, \ldots, n\)
- \(\sum_{i=1}^n x_{ij} = 1\) für alle \(j = 1, 2, \ldots, n\)
Relaxierung: Die Bedingung, dass die \(x_{ij}\) binär sein müssen, kann relaxiert, d. h. fallen gelassen, werden. Zuordnungsprobleme können nämlich als Spezialfälle von Transportproblemen mit \(s_i=1\) und \(d_j=1\) interpretiert werden. Alle, und daher auch die optimalen, Ecken sind daher automatisch ganzzahlig. Daher genügt es \(x_{ij} \geq 0\) für alle \(i\) und \(j\) für kontinuierlichen Variablen \(x_{ij}\) zu fordern.
Algorithmik: Zuordnungsprobleme können mit der Ungarischen Methode sehr effizient gelöst werden. Siehe dazu z. B. Hillier, Lieberman: Introduction to Operations Research. 10th edition, 2015. p. 356 ff.
Modellierungstricks
Neben Dummy-Größen und der Big-M-Methode sind folgende Modellierungstricks interessant:
- Bestimmte Arbeiter können mehr als einer Aufgabe zugeordnet werden: Jeder dieser Arbeiter wird in separate (aber identische) neue Arbeiter aufgespaltet, wobei jedem neuen Arbeiter genau eine Aufgabe zugewiesen wird.
- Eine Aufgabe kann von mehreren Arbeitern ausgeführt werden: Diese Aufgabe wird in separate (aber identische) neue Aufgaben aufgespaltet, wobei jede neue Aufgabe von genau einem Arbeiter ausgeführt wird.
Umladeproblem
Problemstellung
Manchmal schließt der Transport einer Ware die Möglichkeit des Umschlags ein, wobei die Ware über zwischengeschaltete Umschlagspunkte transportiert wird. Dabei können Quellen oder Ziele auch Umschlagspunkte sein. Diese Erweiterung des Transportproblems um die Routing-Entscheidungen wird als Umladeproblem (engl. transshipment problem) bezeichnet. Es ist ein Spezialfall des Minimum-Cost-Flow-Problems, das wiederum ein Spezialfall eines Network-Flow-Problems ist. Umladeprobleme können aber auch in Transportprobleme umformuliert werden.
LP-Formulierung
Wir verwenden die Formulierung als Network Flow Problem: Die Netzwerk-Darstellung des Problems besteht dabei aus einem gerichteten Graphen mit
- Knoten (nodes): alle Quellen (sources), alle Umschlagspunkte (junctions), alle Ziele (targets)
- Kanten (edges): alle erlaubten gerichteten Verbindungen zwischen den Knoten.
Voraussetzung für die Lösbarkeit des Problems ist, dass die Summe der Produktionsmengen aller Quellen gleich der Summe der Bedarfsmengen aller Ziele ist.
Entscheidungsvariablen: Warenmenge \(x_e \geq 0\) auf jeder Kante \(e\)
Zielfunktion: Summe der Kosten \(\sum_{e\in\text{edges}} c_e x_e\)
Nebenbedingungen: Flussbilanz für jeden Knoten
- \(\sum\limits_{\substack{\text{out-edges} \\ o \text{ of } s}} x_o - \sum\limits_{\substack{\text{in-edges} \\ i \text{ of } s}} x_i = \text{production}(s)\) for all sources \(s\)
- \(\sum\limits_{\substack{\text{out-edges} \\ o \text{ of } j}} x_o = \sum\limits_{\substack{\text{in-edges} \\ i \text{ of } j}} x_i\) for all junctions \(j\)
- \(\sum\limits_{\substack{\text{in-edges} \\ i \text{ of } t} } x_i - \sum\limits_{\substack{\text{out-edges} \\ o \text{ of } t} } x_o = \text{demand}(t)\) for all targets \(t\)
Problemklassen
Unter dem Begriff Network Flow Problem werden verschiedene Problemklassen zusammengefasst, siehe z. B. Wikipedia: network flow problem. Manche Autoren verwenden den Begriff Network Flow Problem äquivalent mit Minimum-Cost Flow Problem. Jedes Network Flow Problem kann als LP modelliert werden. In der Graphik Abbildung 5 sind die Problemklassen und ihre Unterklassenstruktur dargestellt.
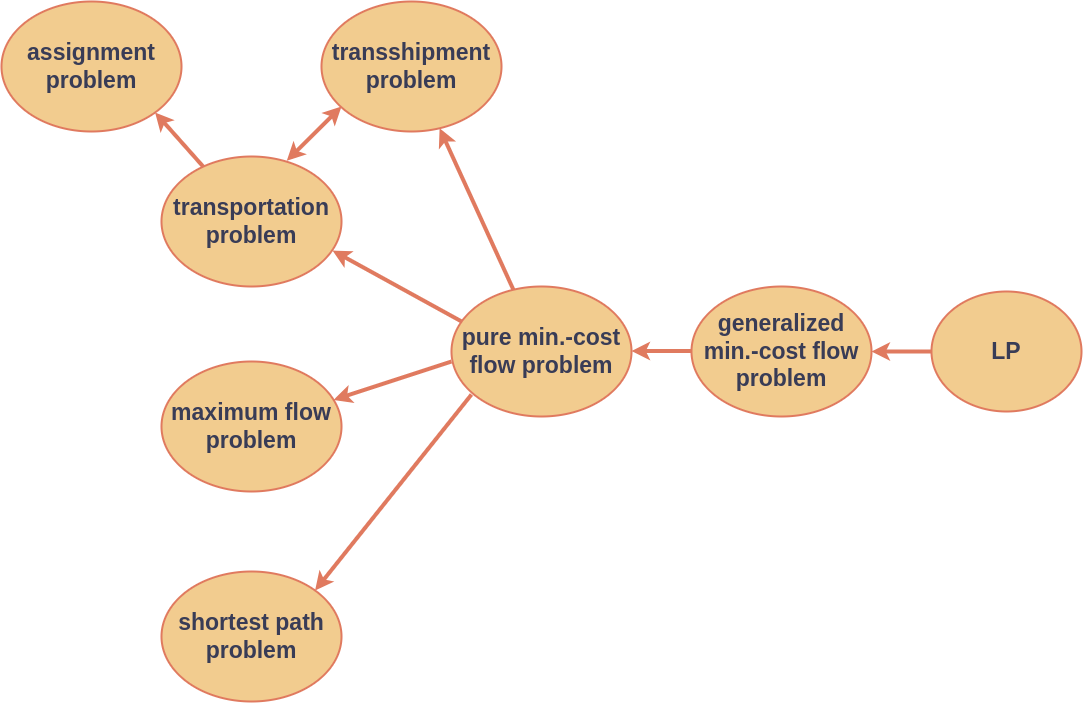
Umformulierungen: Die Unterklassen können als Minimum-Cost Flow Probleme formuliert werden, was den Begriff Unterklasse rechtfertigt. Siehe die Literaturhinweise.
Minimum-Cost Flow Problem
Wir betrachten ein Netzwerk mit Knotenmenge \(N\) (set of nodes) und Kantenmenge \(E\) (set of edges). Das Minimum-Cost Flow Problem (kostenminimaler Fluss) lautet: “Bestimme einen Fluss durch die Kanten, der den Einschränkungen genügt und dessen Gesamtkosten minimal sind.” Das zugehörige LP besteht aus:
- Entscheidungsvariablen: Fluss \(x_e\) durch Kante \(e \in E\)
- Zielfunktion: Minimiere die Summe der Kosten \(\sum\limits_{e \in E} c_e x_e\) mit \(c_e\) den Kosten pro Wareneinheit entlang der Kante \(e\)
- Nebenbedingungen:
- Flussbilanz für jeden Knoten: Summe der Flüsse aus einem Knoten \(n\) in andere Knoten weniger Summe der Flüsse von anderen Knoten in den Knoten \(n\) ist gleich externer Fluss \(b_n\) des Knoten, d. h. \(\sum\limits_{\substack{\text{out-edges} \\ o \text{ of } n} } x_o - \sum\limits_{\substack{\text{in-edges} \\ i \text{ of } n} } x_i = b_n\) für alle Knoten \(n \in N\).
- Kapazitätsbeschränkungen für jede Kante: Jeder Fluss kann nur Werte zwischen seiner unteren und oberen Schranke annehmen, d. h. \(l_e \leq x_e \leq u_e\) für alle Kanten \(e \in E\).
Existenz zulässiger Punkte: Eine notwendige Bedingung dafür, dass es einen zulässigen Punkt gibt, ist, dass \(\sum\limits_{n \in N} b_n = 0\), d. h. der gesamte externe Fluss in das Netzwerk ist gleich dem gesamten externen Fluss aus dem Netzwerk.
Ganzzahlige Lösungen: Wenn alle \(b_n\), \(l_n\) und \(u_n\) ganzzahlig sind, dann ist der vom Simplex-Algorithmus gefundene optimale Punkt auch ganzzahlig, und es müssen keine zusätzlichen Ganzzahligkeitsnebenbedingungen verwendet werden.
Algorithmik: Für Minimum-Cost Flow Probleme gibt es den angepassten und dadurch effizienteren (als der Standard-Simplex-Algorithmus) LP-Algorithmus Network Simplex Algorithm.
Maximaler Fluss
Problemstellung
Ein Maximum Flow Problem kann allgemein wie folgt beschrieben werden:
- Der gesamte Fluss durch ein gerichtetes und zusammenhängendes Netzwerk hat seinen Ursprung an einem Knoten, der Quelle (engl. source) genannt wird, und endet an einem anderen Knoten, der Senke (engl. sink, target) genannt wird.
- Alle übrigen Knoten sind Umladeknoten.
- Der Fluss durch die gerichteten Kanten ist nur in die angegebenen Richtungen erlaubt, wobei die Flussmenge einer Kante durch die Kapazität dieser Kante beschränkt ist. An der Quelle zeigen alle Kanten vom Knoten weg. An der Senke zeigen alle Kanten in den Knoten.
- Das Ziel ist es, die Gesamtmenge des Flusses von der Quelle zur Senke zu maximieren. Diese Größe wird auf eine von zwei äquivalenten Arten gemessen, nämlich entweder die Menge, die die Quelle verlässt oder die Menge, die in die Senke eintritt.
In der Abbildung Abbildung 6 ist der Knoten \(s\) die Quelle und der Knoten \(t\) die Senke.
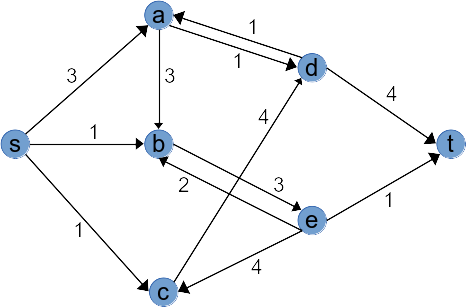
LP-Formulierung
- Entscheidungsvariablen: Fluss \(x_e\) durch Kante \(e \in E\)
- Zielfunktion: Maximiere
- die Summe der Flüsse \(\sum\limits_{\substack{\text{out-edges} \\ o \text{ of } s} } x_o\) aus der Quelle \(s\) oder
- die Summer der Flüsse \(\sum\limits_{\substack{\text{in-edges} \\ i \text{ of } t} } x_i\) in die Senke \(t\)
- Nebenbedingungen:
- Flussbilanz für jeden Knoten \(n\) außer Quelle und Senke: \(\sum\limits_{\substack{\text{out-edges} \\ o \text{ of } n} } x_o = \sum\limits_{\substack{\text{in-edges} \\ i \text{ of } n} } x_i\)
- Kapazitätsbeschränkungen für jede Kante: \(0 \leq x_e \leq u_e\)
Kürzester Weg
Problemstellung
Ein Graph heißt bewertet, wenn jeder Kante ein Gewicht zugeordnet ist. In bewerteten Graphen ist die Länge eines Weges die Summe der Gewichte aller Kanten des Weges. Wir nehmen an, dass alle Kanten-Bewertungen positiv sind, sodass Wege von Knoten zu Knoten immer länger werden.
Dijkstra-Algorithmus
Kürzeste Wege in solchen bewerteten, ungerichteten Graphen können mit dem Algorithmus von Dijkstra gefunden werden, den dieser 1959 formuliert hat. Im Buch Hartmann: “Mathematik für Informatiker: Ein praxisbezogenes Lehrbuch”, Springer, 2019 ist der Algorithmus auf den Seiten 290 ff. ausführlicher beschrieben und begründet. Der Dijkstra-Algorithmus ist kein LP kann auch für gerichtete Graphen formuliert werden, siehe z. B. Wikipedia: Dijkstra’s_algorithm oder GeeksforGeeks: Shortest path in a directed graph by Dijkstra’s algorithm.
LP-Formulierung
Formulierung als Minimum-Cost Flow Problem: Wir betrachten das Shortest Path Problem in einem gerichteten Graphen, das alle kürzesten Wege von einem bestimmten Konten \(S\) zu allen anderen Knoten sucht. Ungerichtete Graphen können als gerichtete interpretiert werden, indem jede ungerichtete Kante durch zwei entgegengesetzte gerichtete Kanten ersetzt wird. Jede dieser gerichteten Kanten erhält dabei das Gewicht der ungerichteten Kante.
- Die Gewichte der Kanten werden als Kosten pro Flussmengeneinheit betrachtet.
- Dem Knoten \(S\) wird der externe Fluss \(n - 1\) zugewiesen mit \(n\) der Anzahl Knoten im Graphen.
- Jedem anderen Knoten wird der externe Fluss \(-1\) zugewiesen.
- Die Kapazität jeder Kante wird unbeschränkt oder mindestens auf \(n - 1\) gesetzt.
Die optimalen Flüsse des damit definierten Minimum-Cost Flow Problems definieren die kürzesten Wege von \(S\) zu allen anderen Knoten. Die Summe der Gewichte entlang dieser Wege sind die zugehörigen kürzesten Distanzen.
Literaturhinweise
- Jensen, Bard: Operations Research Models and Methods. John Wiley & Sons, 2008. Seite 167
- Hillier, Lieberman: Introduction to Operations Research. 10th edition, 2015. ab Seite 397
- Sierksma, Zwols: Linear and Integer Optimization: Theory and Practice. 3rd edition, 2015. Seite 351
