Waschmaschinenstart

Problemstellung

Sie haben einen zeitabhängingen Energiepreis \(c_j\) und wollen den dazu kostenoptimalen Startzeitpunkt für Ihre Waschmaschine finden, sodass der Waschvorgang in den kommenden acht Stunden beendet ist. Der Lastgang des Waschvorgangs und die Preise sind durch die folgenden Daten in Viertelstundenschritten gegeben:

Code 
import numpy as np
import matplotlib.pyplot as plt
import pyomo.environ as pyo
Code 
# time:
T  = 8.0   # h
dt = 0.25  # h
n = int(T/dt)  # number of time periods
times = np.arange(start=0, stop=T + dt, step=dt)
periods = np.arange(start=0, stop=T, step=dt)
time_indices   = range(n + 1)  # 0, 1, ..., n - 1, n
period_indices = range(n)      # 0, 1, ..., n - 1

# load profile:
load_profile = np.array([0.5, 1.0, 1.0, 0.2, 0.2, 1.0])  # kW
# duration of the load profile in number of time periods:
m = len(load_profile) 

# example demand for a given start time:
load_start = 11  # index of starting time of load profile
demand = np.zeros_like(periods)
demand[load_start:load_start + m] = load_profile

# prices:
np.random.seed(0)
noise = np.random.normal(loc=0, scale=0.05, size=n)
price = .15 + 0.2*noise**2 + noise

# plot:
plt.figure(figsize=(5, 4))
plt.subplot(2, 1, 1)
plt.step(periods, demand, where='post', color='black')
plt.xlabel('time (h)')
plt.ylabel('demand (kW)')
plt.grid(True)

plt.subplot(2, 1, 2)
plt.step(periods, price, where='post', color='red')
plt.xlabel('time (h)')
plt.ylabel('price (EUR/kWh)')
plt.grid(True)

plt.tight_layout()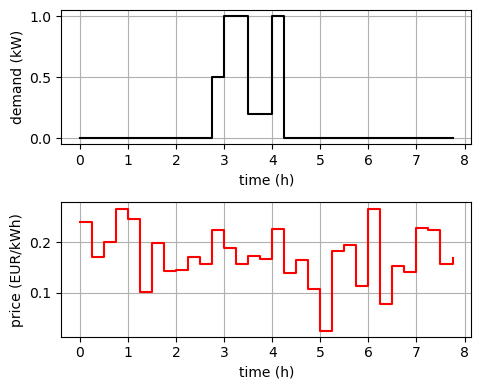

Modellierung

Daten:

  • Samping-Intervall: \(\Delta t\) = 0.25 Stunden
  • Anzahl der Zeitperioden: \(n\) = 8 Stunden / \(\Delta t\) = 32
  • Lastgang der Waschmaschine: \(l_k\) in kW für \(k=0, \dots, m - 1\)
  • Energiepreise: \(c_j\) in EUR/kWh

Entscheidungsvariablen:

  • \(p_j\): Leistungsaufnahme der Waschmaschine in kW während der Zeitperioden \(j = 0, 1, \ldots, n - 1\)
  • \(s_i\): binäre Variablen für \(i = 0, 1, \ldots, n - m\), die angeben, dass die Waschmaschine zum Zeitpunkt \(i\) gestartet wird, falls \(s_i = 1\).

Zielfunktion: \(\min \sum_{j=0}^{n-1} c_j p_j \Delta t\)

Nebenbedingungen:

  • \(\sum_{i=0}^{n - m} s_i = 1\): Die Waschmaschine wird genau einmal gestartet.
  • \(p_j = \sum_{k=0}^{m - 1} l_k s_{j - k}\) für alle \(j = 0, 1, \ldots, n - 1\), falls \(j - k \leq n - m\): Falls die Waschmaschine zum Zeitpunkt \(j - k\) gestartet wurde, dann hat sie in der Zeitperiode \(j\) die Leistungsaufnahme \(l_k\).

Implementierung

Code 
model = pyo.ConcreteModel()

model.J = pyo.Set(initialize=period_indices)
# set of time points where the load profile can be started:
model.S = pyo.Set(initialize=time_indices[:-m])

model.p = pyo.Var(model.J, domain=pyo.NonNegativeReals)  # power in kW
model.s = pyo.Var(model.S, domain=pyo.Binary)  # start load at time/period

model.cost = pyo.Objective(expr=sum(price[j]*model.p[j]*dt 
                for j in model.J), sense=pyo.minimize)

model.one_start = pyo.Constraint(expr=sum(model.s[j] for j in model.S) == 1)

@model.Constraint(model.J)
def demand_constraint(model, j):
    return model.p[j] == sum(load_profile[k]*model.s[j - k] 
                             for k in range(m) 
                             if j - k in model.S)
Code 
solver = pyo.SolverFactory('cbc')
# solver = pyo.SolverFactory('glpk')
# solver = pyo.SolverFactory('appsi_highs')
# solver = pyo.SolverFactory('gurobi')

results = solver.solve(model, tee=False)
print(f"status = {results.solver.status}")
print(f"minimal cost = {pyo.value(model.cost):.2f} EUR")
status = ok
minimal cost = 0.10 EUR
Code 
p_sol_dict = model.p.extract_values()
p_sol = np.array([p_sol_dict[j] for j in period_indices])

s_sol_dict = model.s.extract_values()
s_sol = np.array([s_sol_dict[j] for j in time_indices[:-m]])

plt.figure(figsize=(5, 5))
plt.subplot(3, 1, 1)
plt.stem(times[:-m], s_sol,basefmt=' ',
         markerfmt='.', linefmt='g:')
plt.xlim(0, T)
plt.xlabel('time (h)')
plt.ylabel('start load')
plt.grid(True)

plt.subplot(3, 1, 2)
plt.step(periods, p_sol, where='post', color='black')
plt.xlim(0, T)
plt.xlabel('time (h)')
plt.ylabel('demand (kW)')
plt.grid(True)

plt.subplot(3, 1, 3)
plt.step(periods, price, where='post', color='red')
plt.xlim(0, T)
plt.xlabel('time (h)')
plt.ylabel('price (EUR/kWh)')
plt.grid(True)

plt.tight_layout()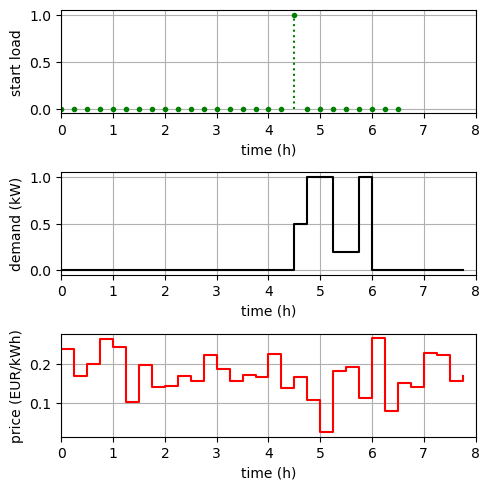

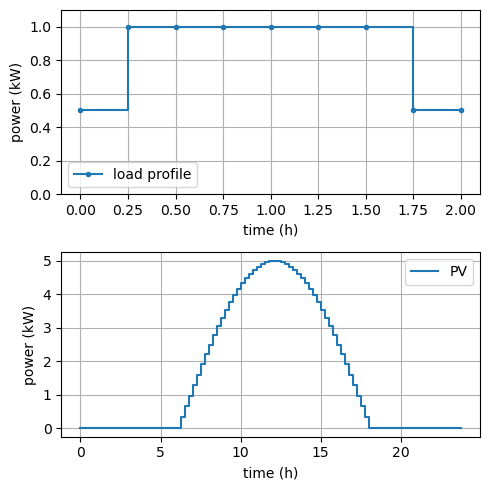
Übung: Power Tracking

Problemstellung

Gegeben ist die Ertragskurve einer PV-Anlage mit 5 kWp über einen Tag. Sie wollen 20 Gabelstapler-Austauschbatterien so laden, dass die Gesamtladekurve möglichst der PV-Ertragskurve folgt. Die Ladekurve einer Batterie und der PV-Ertrag sind durch die Daten unten angegeben.

Das Folgen einer vorgegebenen Leistungskurve wird auch als Power Tracking bezeichnet. Dabei wird der Unterschied zwischen der vorgegebenen Kurve und der nachfahrenden Kurve minimiert. Wir quantifizieren den Unterschied in diesem Beispiel durch die Summe der Beträge der Differenzen zwischen den beiden Kurven: \[ \sum_{j=0}^{n-1} \left| p_{\text{pv},j} - p_{\text{load},j} \right| \] Andere Möglichkeiten, den Unterschied zu quantifizieren sind die Summe der Quadrate der Differenzen oder die maximale absolute Differenz, siehe den Abschnitt Tracking.

Code 
# sampling interval:
dt = 0.25  # h

# load profile for charging a forklift 
load_profile = np.array([0.5, 1, 1, 1, 1, 1, 1, 0.5])  # kW
m = len(load_profile)

# PV power:
T = 24     # h
n = int(T/dt)  # number of time periods
times = np.arange(start=0, stop=T + dt, step=dt)  # timestamps: 0, 0.25, 0.5, ..., 23.75, 24
periods = np.arange(start=0, stop=T, step=dt)     # start times of periods:  0, 0.25, 0.5, ..., 23.75
pv_power = np.zeros_like(periods)
pv_power[6*4:6*4 + 12*4] = 5*np.sin(2*np.pi/(6*4) * periods[:12*4] )  # PV power in kW

plt.figure(figsize=(5, 5))
plt.subplot(2, 1, 1)
load_profile_ = np.hstack((load_profile, load_profile[-1]))
plt.step(np.arange(m + 1)*dt, load_profile_, where='post',
         marker='.', label='load profile')
plt.ylim(0, 1.1*load_profile.max())
plt.xlabel('time (h)')
plt.ylabel('power (kW)')
plt.legend()
plt.grid()

plt.subplot(2, 1, 2)
plt.step(periods, pv_power, where='post', label='PV')
plt.xlabel('time (h)')
plt.ylabel('power (kW)')
plt.legend()
plt.grid()

plt.tight_layout()